Đề thi giữa HK2 môn Toán 7 năm 2021 - Trường THCS Huyền Sơn
-
Hocon247
-
40 câu hỏi
-
60 phút
-
54 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Thời gian làm một bài tập toán (tính bằng phút) của 30 học sinh được ghi lại như sau:
.png)
Giá trị lớn nhất và giá trị nhỏ nhất lần lượt là bao nhiêu?
Giá trị lớn nhất và giá trị nhỏ nhất lần lượt là 14 phút và 5 phút.
Điểm bài thi môn Toán của lớp 7 được cho bởi bảng sau:
.png)
Giá trị lớn nhất và giá trị nhỏ nhất lần lượt là bao nhiêu?
Giá trị lớn nhất và giá trị nhỏ nhất lần lượt là 10 điểm và 3 điểm.
Điềm kiềm tra một tiết môn toán của một lớp 7 được thông kê lại ở bảng dưới đây:
.png)
Tính số trung bình cộng của dấu hiệu (làm tròn đến chữ số thập phân thứ nhất).
Số trung bình cộng của dấu hiệu là:
\(\bar{X}=\frac{2 \cdot 1+3 \cdot 3+4 \cdot 5+5 \cdot 6+6 \cdot 6+7 \cdot 9+8 \cdot 6+9 \cdot 3+10 \cdot 1}{30}=8,2\)
Điểm kiểm tra một tiết môn toán của một lớp 7 được thông kê lại ở bảng dưới đây
.png)
Mốt của dấu hiệu là?
Mốt của dấu hiệu là 7( có tần số lớn nhất)
Ở thành phố Đà Lạt, buổi sáng nhiệt độ là x, buổi trưa nhiệt độ tăng y độ so với buổi sáng, đến chiều tối nhiệt độ lại giảm z độ so với buổi trưa. Hãy biểu thị nhiệt độ của thành phố Đà Lạt vào buổi tối theo các giá trị x, y, z.
Buổi sáng nhiệt độ là x, buổi trưa nhiệt độ tăng y độ so với buổi sáng.
Vậy buổi trưa nhiệt độ là x+y độ.
Đến chiều tối nhiệt độ lại giảm z độ so với buổi trưa.
Vậy nhiệt độ của thành phố Đà Lạt vào buổi tối là x+y–z độ.
Hãy viết biểu thức biểu thị: Diện tích của hình chữ nhật có chiều dài là x (m), chiều dài hơn chiều rộng 3m.
Chiều dài hơn chiều rộng 3m. Chiều dài là x (m). Vậy chiều rộng là x – 3 (m).
Do đó diện tích hình chữ nhật là x(x – 3) (m2).
Hãy viết biểu thức biểu thị: Chu vi hình chữ nhật có chiều rộng là 5m và chiều dài hơn chiều rộng 2m.
Chiều dài hơn chiều rộng 2m. Chiều rộng là 5m. Vậy chiều dài là 7m
Do đó chu vi hình chữ nhật là 2(7 + 5) (m).
Hãy viết lại biểu thức sau cho gọn hơn: \(( - 1)a.b + 1.{a^2}.{b^3}\)
(-1)a.b + 1.a2.b3 = -ab + a2b3
Hãy viết lại biểu thức sau cho gọn hơn: x.3.y + 5.y.z
x.3.y + 5.y.z = 3xy + 5yz
Sân chơi trường của Nam có chiều dài 50m, chiều rộng 30m. Hãy viết biểu thức số biểu thị chu vi sân chơi trường của Nam.
Biểu thức số biểu thị chu vi sân chơi trường của Nam là: (50 + 30).2
Tính giá trị của biểu thức: -x2 + x(y2 + xy) +1 tại x = -2 và y = 1.
Thay x = -2 và y = 1 vào biểu thức
-x2 + x(y2 + xy) +1
Ta có: -(-2)2 + (-2)(1 - 2) +1 = -1
Vậy giá trị của biểu thức -x2 + x(y2 + xy) +1 tại x = -2 và y = 1 là -1.
Cho biểu thức B = -x2 + 2xy + y2 – 1. Hãy tính giá trị của biểu thức B tại x = 0,5 và y=2.
Thay x = 0,5 và y = 2 vào biểu thức
B = -x2 + 2xy + y2 – 1
Ta có: B = -0,52 + 2.0,5.2 + 22 – 1 = 4,75
Vậy giá trị của biểu thức
B = -x2 + 2xy + y2 – 1 tại x = 0,5 và y = 2 là 4,75.
Tính giá trị của biểu thức –m2 + 3 tại m = 3.
Thay m = 3 vào biểu thức –m2 + 3 ta có:
–32 + 3 = –6
Vậy giá trị của biểu thức –m2 + 3 tại m = 3 là –6.
Tính giá trị của biểu thức –m2 + 3 tại m = -2.
Thay m = –2 vào biểu thức –m2 + 3 ta có: –(–2)2 + 3 = –1
Vậy giá trị của biểu thức –m2 + 3 tại m = –2 là –1
Tính giá trị của biểu thức 3m3 – m2 +1 tại m = 3.
Thay m = 3 vào biểu thức 3m3 – m2 +1 ta có: 3.33 – 32 +1 = 73
Vậy giá trị của biểu thức 3m3 – m2 +1 tại m = 3 là 73
Tính giá trị của biểu thức 3m3 – m2 +1 tại m = -2
Thay m = -2 vào biểu thức 3m3 – m2 +1 ta có: 3(-2)3 – (-2)2 + 1 = -27
Vậy giá trị của biểu thức 3m3 – m2 +1 tại m= -2 là -27
Tích của hai đơn thức \(2 x^{2} y z \text { và }-4 x y^{2} z\) là?
Ta có \(2 x^{2} y z \cdot\left(-4 x y^{2} z\right)=-8 x^{3} y^{3} z\)
Kết quả của \(-4 x^{2} y^{3}\left(-\frac{3}{4} x\right) 3 y^{2} x\) là?
Ta có
\(\begin{array}{l} -4 x^{2} y^{3}\left(-\frac{3}{4} x\right) 3 y^{2} x=(-4) \cdot\left(-\frac{3}{4}\right) \cdot 3 x^{2} \cdot x \cdot x \cdot y^{3} \cdot y^{2} \\ =9 \cdot x^{2+1+1} \cdot y^{3+2}=9 x^{4} y^{5} \end{array}\)
Bậc của đơn thức \(\left(-2 x^{3}\right) 3 x^{4} y\) là?
Ta có \(\left(-2 x^{3}\right) 3 x^{4} y=-6 x^{7} y\)
Vậy bậc của đơn thức là 1+7=8
Tích của các đơn thức \(7 x^{2} y^{7},(-3) x^{3} y \text { và }-2\) là
Ta có \(7 x^{2} y^{7} \cdot(-3) x^{3} y \cdot(-2)=42 x^{5} y^{8}\)
Đơn thức đồng dạng với đơn thức \(4 x^{2} y^{2} x\) là
Ta có \(4 x^{2} y^{2} x=4 x^{3} y^{2}\)
Và \(\frac{1}{3} x(-x y)^{2}=\frac{1}{3} x^{3} y^{2}\)
Hai đơn thức có chung phần biến nên là hai đơn thức đồng dạng.
Bậc của đơn thức \(3^{5} x(y z)^{2}\) là
Ta có \(3^{5} x(y z)^{2}=3^{5} x y^{2} z^{2}\)
Vậy bậc của đơn thức là 1+2+2=5
Đơn thức nào sau đây đồng dạng với đơn thức \(5 x^{2} y\) là
Ta thấy đơn thức \(7 x^{2} y\) có phần biến giống với đơn thức đã cho nên là đơn thức đồng dạng.
Đơn thức nào đồng dạng với đơn thức \(-3 x y^{2}\)
Ta có đơn thức \((-3 x y) y=-3 x y^{2}\) là đơn thức đồng dạng với đơn thức đã cho.
Điền đơn thức thích hợp vào chỗ trống \(-7 x^{2} y z^{3}-\cdots=-11 x^{2} y z^{3}\)
Ta có
\(-7 x^{2} y z^{3}-\left(-11 x^{2} y z^{3}\right)=-7 x^{2} y z^{3}+11 x^{2} y z^{3}=4 x^{2} y z^{3}\)
Đơn thức nào không đồng dạng với đơn thức \(\left(-5 x^{2} y^{2}\right)(-2 x y)\)
Ta có \(\left(-5 x^{2} y^{2}\right)(-2 x y)=10 x^{3} y^{3}\)
\(2 x\left(-5 x^{2} y^{2}\right)=-10x^3y^2\)
Hai đơn thức trên không đồng dạng với nhau vì có phần biến khác nhau.
Tổng của các đơn thức \(3 x^{2} y^{3},-5 x^{2} y^{3}, x^{2} y^{3}\) là
Ta có \(3 x^{2} y^{3}-5 x^{2} y^{3}+x^{2} y^{3}=-x^{2} y^{3}\)
Đơn thức nào sau đây đồng dạng với đơn thức \(-3 x^{2} y^{3}\)
Chọn C vì \(\frac{1}{2} x\left(-2 y^{2}\right) x y=-x^{2} y^{3}\) có phần biến giống đơn thức đã cho nên là đơn thức đồng dạng với \(-3 x^{2} y^{3}\)
Cho tam giác ABC có M là trung điểm của BC. Trong các khẳng định sau khẳng định nào đúng?
Nối đoạn thẳng AM.
Xét ΔAMC có: AM
Xét ΔAMB có: AM
Vì M là trung điểm của BC (gt) nên M nằm giữa B và C ta có: CM+MB=BC.
Cộng bất đẳng thức (1) và (2) theo vế với vế ta được:
\( AM + AM < AC + CM + AB + MB \Rightarrow 2AM < AB + \left( {CM + MB} \right) + AC \Rightarrow 2AM < AB + BC + AC \Rightarrow AM < \frac{{AB + BC + AC}}{2}\)
Cho tam giác ABC có hai đường vuông góc BE,CF. So sánh EF và BC.
Gọi M là trung điểm của BC
Xét ΔBCE vuông tại E, M là trung điểm của BC nên \(ME=\frac{1}{2}BC.\)
Xét ΔBCF vuông tại F, M là trung điểm của BC nên
\(MF=\frac{1}{2}BC.\)
Do đó \( ME + MF = \frac{1}{2}BC + \frac{1}{2}BC \Rightarrow ME + MF = BC\) (1)
Ba điểm M,E,F nằm trên ba cạnh của tam giác ABC nên không thể thẳng hàng do đó ba điểm M,E,F tạo thành một tam giác.
Xét ΔMEF có: ME+MF>EF (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra BC>EF.
Cho tam giác ABC có AB > AC. Điểm M là trung điểm của BC. Chọn câu đúng.
Trên tia đối của tia MA ta lấy điểm A′ sao cho MA=MA′.
Xét ΔAMB và ΔA′MC có:
AM=A′M (cách vẽ)
MB=MC (vì M là trung điểm BC)
\( \widehat {AMB} = \widehat {A'MC}(dd)\)
⇒ΔAMB=ΔA′MC(c.g.c)
⇒AB=A′C(hai cạnh tương ứng)
Xét ΔACA′ có: A′C−AC
Mà AB=A′C(cmt); AA′=2AM (theo cách vẽ) nên ta có:
\( \frac{{AB - AC}}{2} < AM < \frac{{AB + AC}}{2}\)
Cho tam giác ABC, trên BC lấy điểm M bất kì nằm giữa B và C. So sánh (AB + AC - BC ) và (2.AM )
.png)
Xét ΔAMB có: AM>AB−BM (bất đẳng thức tam giác)
Xét ΔAMCc ó: AM>AC−MC (bất đẳng thức tam giác)
Vì M nằm giữa B và C (gt) ⇒ BC=BM+MC
Cộng theo từng vế của hai bất đẳng thức trên ta được:
\( 2AM > AB + AC - \left( {BM + MC} \right) \Rightarrow 2AM > AB + AC - BC.\)
Cho tam giác ABC điểm M nằm trong tam giác. So sánh tổng khoảng cách từ M đến ba đỉnh A,B,C với chu vi tam giác ABC.
Nối các đoạn thẳng MA,MB,MC
Áp dụng bất đẳng thức tam giác vào ΔAMB ta được:
MA+MB>AB (1)
Áp dụng bất đẳng thức tam giác vào ΔBMC ta được: MB+MC>BC (2)
Áp dụng bất đẳng thức tam giác vàoΔCMA ta được: MC+MA>CA (3)
Cộng (1), (2) và (3) theo vế với vế ta được:
\(\begin{array}{*{20}{l}} {MA + MB + MB + MC + MC + MA > AB + BC + CA}\\ { \Rightarrow 2\left( {MA + MB + MC} \right) > AB + BC + CA}\\ { \Rightarrow MA + MB + MC > \frac{{AB + BC + CA}}{2}} \end{array}\)
Chọn câu đúng. Trong một tam giác
Gọi độ dài ba cạnh của tam giác là a,b,c. Chu vi tam giác là
\( \frac{{a + b + c}}{2}\)
Ta có:
\(a \(\Rightarrow 2a < a + b + c \Rightarrow a < \frac{{a + b + c}}{2}\)
Tương tự ta cũng có \( b < \frac{{a + b + c}}{2};c < \frac{{a + b + c}}{2}.\)
Nên độ dài một cạnh luôn nhỏ hơn nửa chu vi tam giác.
Cho tam giác ABC vuông ở A có đường cao AD. Lấy H thuộc AD và E thuộc CD sao cho HE // AC Khi đó
.png)
+ Ta có: HE // AC; AC ⊥ AB (do tam giác ABC vuông tại A)
Suy ra HE ⊥ AB (quan hệ từ vuông góc đến song song)
Trong tam giác ABE có:
AD ⊥ BE tại D nên AD là một đường cao của tam giác ABE
HE ⊥ AB nên E, H thuộc một đường cao của tam giác ABE
Mà H = HE ∩ AD
Do đó H là giao của hai đường cao trong tam giác ABE
Nên H là giao của ba đường cao trong tam giác ABE (ba đường cao của một tam giác đồng quy tại một điểm)
Vậy H là trực tâm của tam giác ABE
Suy ra BH ⊥ AE nên đáp án A đúng, đáp án B sai
+ Vì tia AD và tia AE đều nằm trong góc BAC, mà \(\widehat {BAC} = {90^0}\) nên AD không thể vuông góc với AE, do đó đáp án C sai.
+ Vì BH ⊥ AE mà AE ∩ AD = A nên BH không thể vuông góc với AD nên đáp án D sai.
Chọn đáp án A
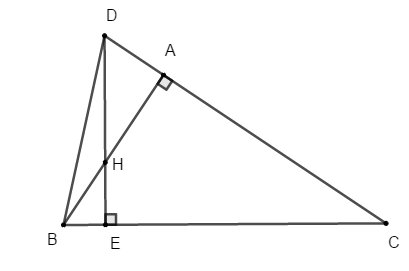
Cho tam giác ABC vuông tại A. Lấy H thuộc AB, vẽ HE ⊥ BC ở E. Tia EH cắt tia CA tại D. Khi đó
Trong tam giác BDC có:
BA ⊥ CD tại A (do tam giác ABC vuông tại A) ⇒ BA là một đường cao của tam giác BDC
DE ⊥ BC tại E (do HE ⊥ BC) ⊥ DE là một đường cao của tam giác BCD
Mà DE ∩ BA = H
Do đó H là giao điểm của hai đường cao trong tam giác BDC
Suy ra H là giao điểm của ba đường cao trong tam giác BDC
Vậy H là trực tâm của tam giác BDC.
Chọn đáp án B
Cho tam giác ABC không cân. Khi đó trực tâm của tam giác ABC là giao điểm của:
Vì tam giác ABC là tam giác không cân nên trực tâm của tam giác ABC là giao điểm của ba đường cao.
Chọn đáp án D
Cho ΔABC cân tại A có AM là đường trung tuyến khi đó
Vì ΔABC cân tại A có AM là đường trung tuyến nên AM cũng là đường cao, đường trung trực và đường phân giác của tam giác ABC
Chọn đáp án D
Cho ΔABC, hai đường cao AM và BN cắt nhau tại H. Em hãy chọn phát biểu đúng:
Vì hai đường cao AM và BN cắt nhau tại H nên CH là đường cao của ΔABC và H là trực tâm tam giác ΔABC nên A, B, D sai, C đúng.
Chọn đáp án C
Cho tam giác ABC cân (không đều) ABC có AB = AC. Hai đường trung trực của hai cạnh AB, AC cắt nhau tại O. Khi đó khẳng định nào sau đây là đúng?
.png)
+ Vì O thuộc đường trung trực của AB nên OA = OB, do đó đáp án A sai
+ Vì ba đường trung trực của tam giác đồng quy tại một điểm nên O là giao điểm của ba đường trung trực của tam giác ABC, suy ra O thuộc đường trung trực cạnh BC
Mà AB = AC nên A thuộc đường trung trực cạnh BC
Do đó AO là đường trung trực của BC , nên đáp án C đúng
+ Lại có tam giác ABC cân tại C (AB = AC) có AO là trung trực nên AO cũng là phân giác của góc BAC
\(= > \widehat {BAO} = \widehat {CAO}\)
Khi đó ΔBAO = ΔCAO (c - g - c)
(Vì AB = AC, AO chung, \(\widehat {BAO} = \widehat {CAO}\))
Suy ra \(\widehat {AOB} = \widehat {AOC}\) => Đáp án B sai
+ Do tam giác ABC là tam giác cân không đều nên O không phải là giao điểm của ba đường phân giác trong tam giác ABC nên O không cách đều ba cạnh của tam giác ABC, do đó đáp án D sai.
Chọn đáp án B

.PNG)
.PNG)
.PNG)
.PNG)