\(\begin{array}{l} {\rm{12: x = 3: 5}}\\ \frac{{12}}{x} = \frac{3}{5}\\ 3.x = 12.5\\ 3x = 60\\ x = 60:3\\ x = 20 \end{array}\)

\(\begin{array}{l} {\left( {\frac{2}{3}} \right)^3}:{\left( { - \frac{2}{3}} \right)^2}\\ = {\left( {\frac{2}{3}} \right)^3}:{\left( {\frac{2}{3}} \right)^2}\\ = {\left( {\frac{2}{3}} \right)^{3 - 2}} = {\left( {\frac{2}{3}} \right)^1}\\ =\frac{2}{3} \end{array}\)

Theo lý thuyết: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì song song với nhau nên ta có b//c

Theo tính chất: Nếu một đường thẳng cắt hai đường thẳng song song thì:

Hai góc đồng vị bằng nhau

Hai góc so le trong bằng nhau.

Hai góc trong  cùng phía bù nhau

Vậy chọn B

\(\begin{array}{l} \frac{{ - 5}}{{17}} \cdot \frac{{31}}{{33}} + \frac{{ - 5}}{{17}} \cdot \frac{2}{{33}} + 1\frac{5}{{17}}\\ = \frac{{ - 5}}{{17}} \cdot \frac{{31}}{{33}} + \frac{{ - 5}}{{17}} \cdot \frac{2}{{33}} + \frac{{22}}{{17}}\\ = \frac{{ - 5}}{{17}} \cdot \left( {\frac{{31}}{{33}} + \frac{2}{{33}}} \right) + \frac{{22}}{{17}}\\ = \frac{{ - 5}}{{17}}.\frac{{33}}{{33}} + \frac{{22}}{{17}}\\ = \frac{{ - 5}}{{17}} + \frac{{22}}{{17}} = \frac{{17}}{{17}} = 1 \end{array}\)

\(\begin{array}{l} \frac{4}{7} + \frac{3}{7} \cdot \left( { - \frac{2}{3}} \right)\\ = \frac{4}{7} + \frac{3}{7} \cdot \left( {\frac{{ - 2}}{3}} \right)\\ = \frac{4}{7} + \frac{{3.\left( { - 2} \right)}}{{7.3}}\\ = \frac{4}{7} + \frac{{ - 6}}{{21}}\\ = \frac{4}{7} - \frac{2}{7} = \frac{2}{7} \end{array}\)

\(\begin{array}{l} \frac{{{9^2} \cdot {3^3}}}{{{3^7}}} \cdot 2018\\ = \frac{{{{\left( {{3^2}} \right)}^2}{{.3}^3}}}{{{3^7}}}.2018\\ = \frac{{{3^4}{{.3}^3}}}{{{3^7}}}.2018\\ = \frac{{{3^7}}}{{{3^7}}}.2018 = 1.2018 = 2018 \end{array}\)

\(\begin{array}{l} \frac{3}{5}x + \frac{2}{3} = \frac{4}{5}\\ \frac{3}{5}x\,\,\,\,\,\,\,\,\,\, = \frac{4}{5} - \frac{2}{3}\\ \frac{3}{5}x\,\,\,\,\,\,\,\,\,\, = \frac{2}{{15}}\\ x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{2}{{15}}:\frac{3}{5}\\ x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{2}{9} \end{array}\)

\(\begin{array}{l} \left| {\frac{1}{2}x + \frac{3}{5}} \right| = \frac{1}{2}\\ \frac{1}{2}x + \frac{3}{5} = \frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,hoặc\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2}x + \frac{3}{5} = - \frac{1}{2}\\ \frac{1}{2}x\,\,\,\,\,\,\,\,\, = \frac{1}{2} - \frac{3}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2}x\,\,\,\,\,\,\,\,\, = - \frac{1}{2} - \frac{3}{5}\\ \frac{1}{2}x\,\,\,\,\,\,\,\,\, = \frac{{ - 1}}{{10}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{2}x\,\,\,\,\,\,\,\,\, \,\,\,\,= \frac{{ - 11}}{{10}}\\ x\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{ - 1}}{{10}}:\frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\, = \frac{{ - 11}}{{10}}:\frac{1}{2}\\ x\,\,\,\,\,\,\,\,\,\, \,\,\,= \frac{{ - 1}}{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\, = \frac{{ - 11}}{5} \end{array}\)

\(\begin{array}{l} {2^x} + {2^{x + 4}} = 544\\ {2^x} + {2^x}{.2^4} = 544\\ {2^x}.\left( {1 + {2^4}} \right) = 544\\ {2^x}.17 = 544\\ {2^x} = 544:17\\ {2^x} = 32\\ {2^x} = {2^5}\\ x = 5 \end{array}\)

Gọi x, y, z (x>0, y>0, z>0) lần lượt là số bi xanh, bi đỏ và bi vàng.

Theo đề bài ta có

Số viên bi màu xanh và đỏ tỉ lệ với 2 và 3 nên:

\(x:y = 2:3 \Rightarrow \frac{x}{2} = \frac{y}{3}\)

số viên bi màu đỏ và vàng tỉ lệ với 4 và 5 nên :

\(y:z = 4:5 \Rightarrow \frac{y}{4} = \frac{z}{5}\)

Ta có 

\(\frac{x}{2} = \frac{y}{3} \Rightarrow \frac{1}{4}.\frac{x}{2} = \frac{1}{4}\frac{y}{3} \Rightarrow \frac{x}{8} = \frac{y}{{12}}\,\,\,(1)\)

\(\frac{y}{4} = \frac{z}{5} \Rightarrow \frac{1}{3}.\frac{y}{4} = \frac{1}{3}.\frac{z}{5} \Rightarrow \frac{y}{{12}} = \frac{z}{{15}}\,\,\,\,(2)\)

Từ (1) và (2) \(\Rightarrow \frac{x}{8} = \frac{y}{{12}} = \frac{z}{{15}}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\begin{array}{l} \frac{x}{8} = \frac{y}{{12}} = \frac{z}{{15}} = \frac{{x + y + z}}{{35}} = \frac{{35}}{{35}} = 1\\ \frac{x}{8} = 1 \Rightarrow x = 8\\ \frac{y}{{12}} = 1 \Rightarrow y = 12\\ \frac{z}{{15}} = 1 \Rightarrow z = 15 \end{array}\)

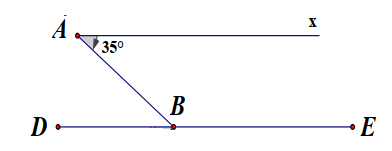
Ta có

\(\begin{array}{l} \left\{ \begin{array}{l} Ax//DE\\ \widehat {xAB}\,\,và\,\,\widehat {ABE}\text{ nẳm ở vị trí trong cùng phía} \end{array} \right.\\ \Rightarrow \widehat {xAB} + \widehat {ABE} = {180^0}\\ \widehat {ABE} = {180^0} - \widehat {xAB} = {180^0} - {35^0} = {145^0} \end{array}\)

A đúng theo tính chất hai đường thẳng song song.

B sai: Đường trung trực của đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của đoạn thẳng.

C sai: Qua điểm A nằm ngoài đường thẳng a, có duy nhất một đường thẳng song song với a.

D sai: Hai góc  đối đỉnh thì bằng nhau.

\( \begin{array}{l} \frac{1}{2}x - \frac{1}{2} = \frac{2}{7}\\ \frac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \frac{2}{7} + \frac{1}{2}\\ \frac{1}{2}x\,\,\,\,\,\,\,\,\,\, = \frac{{11}}{{14}}\\ x\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{11}}{{14}}:\frac{1}{2}\\ x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{11}}{{14}}.2\\ x \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= \frac{{11}}{7} \end{array}\)

\(\begin{array}{*{20}{l}} {{\rm{|x - 3,5| = 5,5}}}\\ {x - 3,5 = 5,5{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} hoặc{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x - 3,5 = - 5,5}\\ {x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\, = 5,5 + 3,5{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\, = - 5,5 + 3,5{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} }\\ {x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = 9\,\,\,\,\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = - 2}\\ \end{array}\)

Gọi x,  y, z lần lượt là số học sinh lớp 7A, 7B, 7C

Theo đề bài ta có

\(x:y:z = 7:8:9 \Rightarrow \frac{x}{7} = \frac{y}{8} = \frac{z}{9}\)

Áp dụng tính chất dãy tỉ số bằng nhau

\(\begin{array}{l} \frac{x}{7} = \frac{y}{8} = \frac{z}{9} = \frac{{y - z}}{{8 - 7}} = 3\\ Với\,\,\frac{x}{7} = 3 \Rightarrow x = 21\\ Với\,\,\frac{y}{8} = 3 \Rightarrow y = 24\\ Với \,\,\frac{z}{9} = 3 \Rightarrow z = 27 \end{array}\)

Vậy số học sinh lớp 7A là 21 bạn 

 số học sinh lớp 7B là 24 bạn 

 số học sinh lớp 7C là 27 bạn 

\(\frac{{{3^5} \cdot {4^2}}}{{{2^3} \cdot 9 \cdot 5}} = \frac{{{3^5}.{{\left( {{2^2}} \right)}^2}}}{{{2^3}{{.3}^2}.5}} = \frac{{{3^5}{{.2}^4}}}{{{3^2}{{.2}^3}.5}} = \frac{{{3^3}.2}}{{1.1.5}} = \frac{{54}}{5}\)

\(\begin{array}{l} \frac{6}{{15}} \cdot \frac{3}{4} - \frac{6}{{15}} \cdot \frac{2}{{11}}\\ = \frac{6}{{15}} \cdot \left( {\frac{3}{4} - \frac{2}{{11}}} \right)\\ = \frac{6}{{15}}.\frac{{25}}{{44}} = \frac{5}{{22}} \end{array}\)

\(\frac{1}{4} \cdot \frac{3}{{11}} - \frac{5}{{22}} = \frac{3}{{44}} - \frac{5}{{22}} = \frac{{ - 7}}{{44}}\)

\(\begin{array}{l} {\rm{2,5 - 3,9 - 1,5 - 2,5 + 3,9}}\\ = \left( {2,5 - 2,5} \right) - \left( {3,9 - 3,9} \right) - 1,5\\ = - 1,5 \end{array}\)

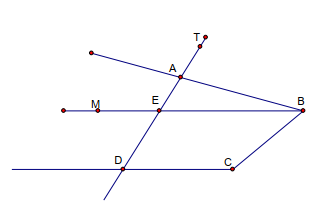
Hai góc đồng vị là \(\widehat{TAB}\,\,và\,\,\widehat{CDT}\)

Câu B: \(\widehat{TAE}\,\,và\,\,\widehat{CDT}\) là hai góc trong cùng phía

Câu C: \(\widehat{MED}\,\,và\,\,\widehat{EDC}\) là hai góc so le trong

Câu D: \(\widehat{BED}\,\,và\,\,\widehat{EDC}\) là hai góc trong cùng phía

\(\begin{array}{l} \frac{{x - 1}}{{x + 2}} = \frac{{x - 2}}{{x + 3}}\,\,(1)\\ \left( {x - 1} \right)\left( {x + 3} \right) = \left( {x - 2} \right)\left( {x + 2} \right)\\ \left( {x - 1} \right).x + \left( {x - 1} \right).3 = \left( {x - 2} \right).x + \left( {x - 2} \right).2\\ x.x - x.1 + x.3 - 3 = x.x - 2.x + 2x - 2.2\\ {x^2} - x + 3x - 3 = {x^2} - 2x + 2x - 4\\ {x^2} + 2x - 3 = {x^2} - 4\\ {x^2} + 2x - 3 - {x^2} + 4 = 0\\ 2x + 1 = 0\\ 2x = - 1\\ x = \frac{{ - 1}}{2} \end{array}\)Thể \(x=\frac{-1}{2}\) vào (1) ta thấy x thỏa nên giá trị của x là \(x=\frac{-1}{2}\)

\(\begin{array}{l} \frac{3}{{15}} - \left[ {\frac{1}{5} - \left( {\frac{2}{3} - \frac{2}{5}} \right)} \right]\\ = \frac{3}{{15}} - \left[ {\frac{1}{5} - \frac{4}{{15}}} \right]\\ = \frac{3}{{15}} - \left( {\frac{{ - 1}}{{15}}} \right)\\ = \frac{3}{{15}} + \frac{1}{{15}}\\ = \frac{4}{{15}} \end{array}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeWaaeWaa8aabaWdbmaalaaa % paqaa8qacqGHsislcqaIXaqma8aabaWdbiabikdaYaaaaiaawIcaca % GLPaaapaWaaWbaaSqabeaacqaIYaGmaaGcpeGaey4kaSYaaeWaa8aa % baWdbmaalaaapaqaa8qacqaIYaGma8aabaWdbiabiodaZaaaaiaawI % cacaGLPaaapaWaaWbaaSqabeaacqaIZaWmaaaakeaacqGH9aqpdaWc % aaqaamaabmaabaGaeyOeI0IaeGymaedacaGLOaGaayzkaaWaaWbaaS % qabeaacqaIYaGmaaaakeaacqaIYaGmdaahaaWcbeqaaiabikdaYaaa % aaGccqGHRaWkdaWcaaqaaiabikdaYmaaCaaaleqabaGaeG4mamdaaa % GcbaGaeG4mamZaaWbaaSqabeaacqaIZaWmaaaaaaGcbaGaeyypa0Za % aSaaaeaacqaIXaqmaeaacqaI0aanaaGaey4kaSYaaSaaaeaacqaI4a % aoaeaacqaIYaGmcqaI3aWnaaaabaGaeyypa0ZaaSaaaeaacqaI1aqn % cqaI5aqoaeaacqaIXaqmcqaIWaamcqaI4aaoaaaaaaa!60DC! \begin{array}{l} {\left( {\frac{{ - 1}}{2}} \right)^2} + {\left( {\frac{2}{3}} \right)^3}\\ = \frac{{{{\left( { - 1} \right)}^2}}}{{{2^2}}} + \frac{{{2^3}}}{{{3^3}}}\\ = \frac{1}{4} + \frac{8}{{27}}\\ = \frac{{59}}{{108}} \end{array}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeWaaSaaa8aabaWdbiabdIha % 4bWdaeaapeGaeG4mamdaaiabg2da9maalaaapaqaa8qacqWG5bqEa8 % aabaWdbiabiwda1aaaaeaacqGHshI3daWcaaqaaiabdIha4jabc6ca % UiabdIha4bqaaiabiodaZaaacqGH9aqpdaWcaaqaaiabdIha4jabc6 % caUiabdMha5bqaaiabiwda1aaaaeaacqGHshI3daWcaaqaaiabdIha % 4naaCaaaleqabaGaeGOmaidaaaGcbaGaeG4mamdaaiabg2da9maala % aabaGaeGOnayJaeGimaadabaGaeGynaudaaaqaaiabgkDiEpaalaaa % baGaemiEaG3aaWbaaSqabeaacqaIYaGmaaaakeaacqaIZaWmaaGaey % ypa0JaeGymaeJaeGOmaidabaGaeyO0H4TaemiEaG3aaWbaaSqabeaa % cqaIYaGmaaGccqGH9aqpcqaIZaWmcqaI2aGnaeaacqGHshI3cqWG4b % aEcqGH9aqpcqaI2aGncqWGObaAcqWGVbWBcqWGHbqycqWGJbWycqWG % 4baEcqGH9aqpcqGHsislcqaI2aGnaeaacqWG4baEcqGH9aqpcqaI2a % GncqGHshI3cqaI2aGncqGGUaGlcqWG5bqEcqGH9aqpcqaI2aGncqaI % WaamcqGHshI3cqWG5bqEcqGH9aqpcqaIXaqmcqaIWaamaeaacqWG4b % aEcqGH9aqpcqGHsislcqaI2aGncqGHshI3cqGHsislcqaI2aGncqGG % UaGlcqWG5bqEcqGH9aqpcqaI2aGncqaIWaamcqGHshI3cqWG5bqEcq % GH9aqpcqGHsislcqaIXaqmcqaIWaamaaaa!A1AE! \begin{array}{l} \frac{x}{3} = \frac{y}{5}\\ \Rightarrow \frac{{x.x}}{3} = \frac{{x.y}}{5}\\ \Rightarrow \frac{{{x^2}}}{3} = \frac{{60}}{5}\\ \Rightarrow \frac{{{x^2}}}{3} = 12\\ \Rightarrow {x^2} = 36\\ \Rightarrow x = 6\,\,hoặc\,\,x = - 6\\ với\,\,x = 6 \Rightarrow 6.y = 60 \Rightarrow y = 10\\ với\,\,x = - 6 \Rightarrow - 6.y = 60 \Rightarrow y = - 10 \end{array}\)

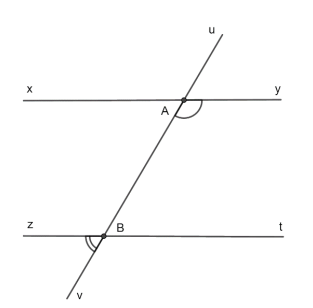
\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeWaaiqaaqaabeqaaiabdIha % 4jabdMha5jabc+caViabc+caViabdQha6jabdsha0bqaamaaHaaaba % GaemyEaKNaemyqaeKaemOqaieacaGLcmaacqWG2bGDcqWGHbqydaqi % aaqaaiabdgeabjabdkeacjabdsha0bGaayPadaGaemiDaqNaemOCai % Naem4Ba8MaemOBa4Maem4zaCgaaiaawUhaaaqaaiabgkDiEpaaHaaa % baGaemyEaKNaemyqaeKaemOqaieacaGLcmaacqGHRaWkdaqiaaqaai % abdgeabjabdkeacjabdsha0bGaayPadaGaeyypa0JaeGymaeJaeGio % aGJaeGimaaZaaWbaaSqabeaacqaIWaamaaaakeaacqGHshI3daqiaa % qaaiabdgeabjabdkeacjabdsha0bGaayPadaGaeyypa0JaeGymaeJa % eGioaGJaeGimaaZaaWbaaSqabeaacqaIWaamaaGccqGHsisldaqiaa % qaaiabdMha5jabdgeabjabdkeacbGaayPadaGaeyypa0JaeGymaeJa % eGioaGJaeGimaaZaaWbaaSqabeaacqaIWaamaaGccqGHsislcqaIXa % qmcqaIXaqmcqaIWaamdaahaaWcbeqaaiabicdaWaaakiabg2da9iab % iEda3iabicdaWmaaCaaaleqabaGaeGimaadaaaaaaa!861D! \begin{array}{l} \left\{ \begin{array}{l} xy//zt\\ \widehat {yAB}\,\,và\,\,\widehat {ABt}\text{ nằm ở vị trí trong cùng phía } \end{array} \right.\\ \Rightarrow \widehat {yAB} + \widehat {ABt} = {180^0}\\ \Rightarrow \widehat {ABt} = {180^0} - \widehat {yAB} = {180^0} - {110^0} = {70^0} \end{array}\)

Lại có

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % Waaqaafaaakqaabeaeaaaaaaaaa8qabaWaaecaaeaacqWG6bGEcqWG % cbGqcqWG2bGDaiaawkWaaiabdAha2jabdggaHnaaHaaabaGaemyqae % KaemOqaiKaemiDaqhacaGLcmaaaeaadaqiaaqaaiabdQha6jabdkea % cjabdAha2bGaayPadaGaeyypa0ZaaecaaeaacqWGbbqqcqWGcbGqcq % WG0baDaiaawkWaaiabg2da9iabiEda3iabicdaWmaaCaaaleqabaGa % eGimaadaaaaaaa!550C! \begin{array}{l} \widehat {zBv}\,\,và\,\,\widehat {ABt}\text{ đối đỉnh}\\ \Rightarrow\widehat {zBv} = \widehat {ABt} = {70^0} \end{array}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeGaemOqaiKaeyypa0ZaaeWa % a8aabaWdbmaalaaabaGaeGynaudabaGaeGOmaidaaiabgkHiTiabig % daXaGaayjkaiaawMcaa8aadaahaaWcbeqaa8qacqaIZaWmaaGccqGH % RaWkdaqadaWdaeaapeWaaSaaaeaacqaIZaWmaeaacqaIYaGmaaGaey % OeI0YaaSaaa8aabaWdbiabigdaXaWdaeaapeGaeGOmaidaaaGaayjk % aiaawMcaa8aadaahaaWcbeqaa8qacqaIXaqmcqaIZaWmaaGccqGHsi % sldaWcaaqaaiabiEda3aqaaiabisda0aaaaeaacqGH9aqpdaqadaqa % amaalaaabaGaeG4mamdabaGaeGOmaidaaaGaayjkaiaawMcaamaaCa % aaleqabaGaeG4mamdaaOGaey4kaSIaeGymaeZaaWbaaSqabeaacqaI % XaqmcqaIZaWmaaGccqGHsisldaWcaaqaaiabiEda3aqaaiabisda0a % aaaeaacqGH9aqpdaWcaaqaaiabiodaZmaaCaaaleqabaGaeGOmaida % aaGcbaGaeGOmaiZaaWbaaSqabeaacqaIYaGmaaaaaOGaey4kaSIaeG % ymaeJaeyOeI0YaaSaaaeaacqaI3aWnaeaacqaI0aanaaaabaGaeyyp % a0ZaaSaaaeaacqaI5aqoaeaacqaI0aanaaGaey4kaSIaeGymaeJaey % OeI0YaaSaaaeaacqaI3aWnaeaacqaI0aanaaaabaGaeyypa0ZaaSaa % aeaacqaIXaqmcqaIZaWmaeaacqaI0aanaaGaey4kaSYaaSaaaeaacq % aI3aWnaeaacqaI0aanaaGaeyypa0ZaaSaaaeaacqaIYaGmcqaIWaam % aeaacqaI0aanaaGaeyypa0JaeGynaudaaaa!7BEE! \begin{array}{l} B = {\left( {\frac{5}{2} - 1} \right)^3} + {\left( {\frac{3}{2} - \frac{1}{2}} \right)^{13}} - \frac{7}{4}\\ = {\left( {\frac{3}{2}} \right)^3} + {1^{13}} - \frac{7}{4}\\ = \frac{{{3^2}}}{{{2^2}}} + 1 - \frac{7}{4}\\ = \frac{9}{4} + 1 - \frac{7}{4}\\ = \frac{{13}}{4} + \frac{7}{4} = \frac{{20}}{4} = 5 \end{array}\)

\(% MathType!MTEF!2!1!+- % feaahqart1ev3aaatCvAUfKttLearuGlw5gvP1wzaeXatLxBI9gBam % XvP5wqSXMqHnxAJn0BKvguHDwzZbqegm0B1jxALjhiov2DaeHbuLwB % Lnhiov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFf % euY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9 % q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqaba % WaaqaafaaakqaabeqaaabaaaaaaaaapeGaemiEaG3aaWbaaSqabeaa % cqaIZaWmaaGccqGH9aqpcqaIYaGmcqaI3aWnaeaacqWG4baEdaahaa % WcbeqaaiabiodaZaaakiabg2da9iabiodaZmaaCaaaleqabaGaeG4m % amdaaaGcbaGaemiEaGNaeyypa0JaeG4mamdaaaa!49F8! \begin{array}{l} {x^3} = 27\\ {x^3} = {3^3}\\ x = 3 \end{array}\)

Do -1<0 nên không tìm được giá trị của x

C sai vì \(\frac{a}{b}=\frac{3}{4}\Rightarrow a.4=b.3\)