Thay tọa độ các điểm vào phương trình \(y = f\left( x \right)\)

Có \({1^3} - {3.1^2} + 2 = 0\)\( \Rightarrow P\left( {1;0} \right)\) thuộc đồ thị hàm số \(y = f\left( x \right)\).

Hình chóp n-giác có \(n + 1\) mặt.

Hình chóp tứ giác có 5 mặt

Hàm f đổi dấu từ dương sang âm qua \({x_0}\) thì đạt cực đại tại \({x_0}\)

Hàm f đổi dấu từ âm sang dương qua \({x_0}\) thì đạt cực tiểu tại \({x_0}\)

Vậy hàm f đổi dấu từ dương sang âm qua \(x = 0\) thì đạt cực đại tại \(x = 0\).

Chọn B

Thể tích hình chóp có diện tích đáy B, chiều cao h là: \(V = \dfrac{1}{3}B.h\)

Thể tích hình chóp có diện tích đáy bằng 4, chiều cao bằng 3 là: \(V = 4.3 = 12\)

\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{x + 1}}{{x - 2}} =  + \infty \)

Tiệm cận đứng của hàm số \(y = \dfrac{{x + 1}}{{x - 2}}\) là \(x = 2\)

\(\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{x + 1}}{{x - 2}} = 1\)\( \Rightarrow y = 1\) là đường tiệm cận ngang.

Thể tích hình lập phương cạnh a: \(V = {a^3}\)

Thể tích lập phương cạnh 2 là: \(V = 8\)

Tập xác định: \(D = \mathbb{R}{\rm{\backslash }}\left\{ { - 7} \right\}\).

\(\begin{array}{l}y' = \dfrac{{ - 2\left( {x + 7} \right) - \left( {3 - 2x} \right)}}{{{{\left( {x + 7} \right)}^2}}}\\ = \dfrac{{ - 17}}{{{{\left( {x + 7} \right)}^2}}} < 0\forall x \in D\end{array}\)

\( \Rightarrow \)Hàm số nghịch biến trên \(\left( { - \infty ; - 7} \right)\) và \(\left( { - 7; + \infty } \right)\)

\(y' = 4{x^3} + 4x = 4x\left( {{x^2} + 1} \right)\)

\(y' = 0 \Leftrightarrow x = 0\)

Bảng biến thiên:

\( \Rightarrow \) Hàm số có 1 điểm cực trị.

Ta có \(y' = 2x - 2\)

\(y' = 0 \Leftrightarrow x = 1 \in \left[ {0;3} \right]\)

\(f\left( 0 \right) = 3,f\left( 3 \right) = 6\)

\(\mathop {\min }\limits_{\left[ {0;3} \right]} y = f\left( 1 \right) = 2\)

Đồ thị trên là đồ thị của hàm số trùng phương.

\(\mathop {\lim }\limits_{x \to  + \infty } y =  + \infty  \Rightarrow a > 0\). \( \Rightarrow \)C, D sai.

Hàm số có các điểm cực trị là: \(x = 0;x =  \pm 1\). \( \Rightarrow \)A sai.

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có TCĐ là \(x = 1\) \( \Rightarrow \) loại đáp án A.

Đồ thị hàm số đi qua điểm \(\left( { - 1;{\mkern 1mu} {\mkern 1mu} 0} \right)\) và \(\left( {0; - 1} \right)\) \( \Rightarrow \) chọn đáp án B.

Chọn B.

Phương trình trục hoành: \(y = 0\).

Ta có \(y' = 4{x^3} - 4x \Rightarrow \) Hệ số góc của tiếp tuyến tại điểm có hoành độ \(x = {x_0}\) là \(y'\left( {{x_0}} \right) = 4x_0^3 - 4{x_0}\).

Tiếp tuyến // Ox \( \Rightarrow y'\left( {{x_0}} \right) = 0 \Leftrightarrow 4x_0^3 - 4{x_0} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{x_0} = {\rm{\;}} \pm 1}\end{array}} \right.\).

Khi \(x =  \pm 1\) ta tìm được hai tiếp tuyến trùng nhau là  \(y =  - 3\)

Vậy có hai tiếp tuyến song song với trục hoành.

Chọn C.

Dựa vào BBT ta thấy hàm số nghịch biến trên các khoảng \(\left( { - \infty ;{\mkern 1mu} {\mkern 1mu}  - 2} \right)\) và \(\left( {0;{\mkern 1mu} {\mkern 1mu} 2} \right).\)

Chọn C.

Dựa vào hình vẽ ta nhận thấy hàm số đồng biến trên \(\left( { - 2; - 1} \right)\).

Chọn A.

Hình lập phương có \(6\) mặt, \(8\) đỉnh và 12 cạnh nên tổng số cạnh, mặt đỉnh là: \(6 + 8 + 12 = 26\).

Chọn A.

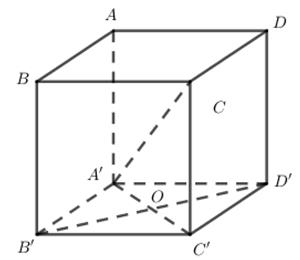
Ta có

\(\begin{array}{*{20}{l}}{\rm{\;}}&{BB'//CC' \Rightarrow BB'//\left( {ACC'} \right) \supset AC'}\\{\rm{\;}}&{ \Rightarrow d\left( {AC';BB'} \right) = d\left( {BB';\left( {ACC'} \right)} \right) = d\left( {B';\left( {ACC'} \right)} \right)}\end{array}\)

Gọi \(O = A'C' \cap B'D'\) ta có :

 \(\left\{ {\begin{array}{*{20}{l}}{\rm{\;}}&{B'O \bot A'C'}\\{\rm{\;}}&{B'O \bot CC'}\end{array}} \right. \Rightarrow B'O \bot \left( {ACC'} \right) \Rightarrow d\left( {B';\left( {ACC'} \right)} \right) = B'O\)

Tam giác A’B’D’ là tam giác đều cạnh a

\( \Rightarrow B'D' = a \Rightarrow B'O = \dfrac{a}{2}\)

Chọn C.

TXĐ: \(D = R\backslash \left\{ 1 \right\}\)

Ta có: \(\mathop {\lim }\limits_{x \to \infty } \dfrac{{2x - 3}}{{x - 1}} = 2 \Rightarrow y = 2\) là TCN của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to 1} \dfrac{{2x - 3}}{{x - 1}} = \infty {\rm{\;}} \Rightarrow x = 1\) là TCĐ của đồ thị hàm số.

Chọn A.

Ta có \(f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {2 - x} \right)\left( {x + 3} \right).\)

Lập bảng xét dấu ta có:

Dựa vào bảng biến thiên ta thấy:

Hàm số đồng biến trên \(\left( { - 3;2} \right)\)và nghịch biến trên \(\left( { - \infty ; - 3} \right),\left( {2; + \infty } \right).\)

Chọn D.

Đk: \(x \ne 1\).

Ta có: \(y' = \dfrac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}}\).

Hoành độ của các điểm thuộc đồ thị hàm số mà tiếp tuyến tại đó có hệ số góc bằng 2018 là nghiệm của phương trình

\(\dfrac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} = 2018\) (vô nghiệm) nên không có điểm nào thỏa mãn.

Chọn B.

Xét phương trình hoành độ giao điểm \({x^4} - 2{x^2} + 1 = 1\) \( \Leftrightarrow {x^4} - 2{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \sqrt 2 }\\{x = {\rm{\;}} - \sqrt 2 }\end{array}} \right.\).

Vậy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = {x^4} - 2{x^2} + 1\) tại 3 điểm phân biệt

Chọn C.

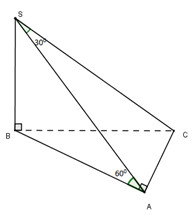
Ta có:\(\left. {\begin{array}{*{20}{l}}{AC \bot AB}\\{AC \bot SB{\mkern 1mu} {\mkern 1mu} \left( {SB \bot \left( {ABC} \right)} \right)}\end{array}} \right\}\)\( \Rightarrow AC \bot \left( {SAB} \right) \Rightarrow AC \bot SA\)   

\( \Rightarrow \) SA là hình chiếu vuông góc của SC trên (SAB) ⇒\(\widehat {\left( {SC;\left( {SAB} \right)} \right)} = \widehat {\left( {SC;SA} \right)} = \widehat {CSA} = {30^0}\)

\(\left. {\begin{array}{*{20}{l}}{\left( {SAC} \right) \cap \left( {ABC} \right) = AC}\\{\left( {SAC} \right) \supset SA \bot AC}\\{\left( {ABC} \right) \supset AB \bot AC}\end{array}} \right\}\)\( \Rightarrow \widehat {\left( {\left( {SAC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SA;AB} \right)} = \widehat {SAB} = {60^0}\)

\(SB \bot \left( {ABC} \right) \Rightarrow SB \bot AB \Rightarrow \Delta SAB\) vuông tại B

\( \Rightarrow AB = SB.cot60 = a.\dfrac{1}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3}\)

\( \Rightarrow SA = \sqrt {S{B^2} + A{B^2}} {\rm{\; = }}\sqrt {{a^2} + \dfrac{{{a^2}}}{3}} {\rm{\;}} = \dfrac{{2a}}{{\sqrt 3 }}\)

Xét tam giác vuông SAC ta có: \(AC = SA.\tan 30 = \dfrac{{2a}}{{\sqrt 3 }}.\dfrac{1}{{\sqrt 3 }} = \dfrac{{2a}}{3}\)

⇒ \({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}\dfrac{{a\sqrt 3 }}{3}.\dfrac{{2a}}{3} = \dfrac{{{a^2}\sqrt 3 }}{9}\)

⇒ \({V_{S.ABC}} = \dfrac{1}{3}SB.{S_{ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{9} = \dfrac{{{a^3}\sqrt 3 }}{{27}}\)

Chọn A.

TXĐ: \(x \ge {\rm{\;}} - \dfrac{1}{3};{\mkern 1mu} {\mkern 1mu} x \ne 1;{\mkern 1mu} {\mkern 1mu} x \ne 2\). Ta có:

\(\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to  + \infty } y = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}} = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{\dfrac{1}{x} + \dfrac{1}{{{x^2}}} - \sqrt {\dfrac{3}{{{x^3}}} + \dfrac{1}{{{x^4}}}} }}{{1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}}} = 0}\\{\mathop {\lim }\limits_{x \to  - \infty } y = \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}} = \mathop {\lim }\limits_{x \to  - \infty } \dfrac{{\dfrac{1}{x} + \dfrac{1}{{{x^2}}} - \sqrt {\dfrac{3}{{{x^3}}} + \dfrac{1}{{{x^4}}}} }}{{1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}}} = 0}\end{array}\)

Do đó đồ thị hàm số có TCN \(y = 0\).

\(\begin{array}{*{20}{l}}\begin{array}{l}y = \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}}\\ = \dfrac{{\left( {x + 1 - \sqrt {3x + 1} } \right)\left( {x + 1 + \sqrt {3x + 1} } \right)}}{{\left( {x + 1 + \sqrt {3x + 1} } \right)\left( {{x^2} - 3x + 2} \right)}}\\ = \dfrac{{{{\left( {x + 1} \right)}^2} - \left( {3x + 1} \right)}}{{\left( {x + 1 + \sqrt {3x + 1} } \right)\left( {{x^2} - 3x + 2} \right)}}\end{array}\\\begin{array}{l} = \dfrac{{{x^2} - x}}{{\left( {x + 1 + \sqrt {3x + 1} } \right)\left( {{x^2} - 3x + 2} \right)}}\\ = \dfrac{{x\left( {x - 1} \right)}}{{\left( {x + 1 + \sqrt {3x + 1} } \right)\left( {x - 1} \right)\left( {x - 2} \right)}}\\ = \dfrac{x}{{\left( {x + 1 + \sqrt {3x + 1} } \right)\left( {x - 2} \right)}}\end{array}\end{array}\)

Ta có

\(\begin{array}{*{20}{l}}{\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \dfrac{x}{{\left( {x + 1 + \sqrt {3x + 1} } \right)\left( {x - 2} \right)}} =  + \infty }\\{\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \dfrac{x}{{\left( {x + 1 + \sqrt {3x + 1} } \right)\left( {x - 2} \right)}} =  - \infty }\end{array}\), do đó đồ thị hàm số có TCĐ .

Xét phương trình

\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x + 1 + \sqrt {3x + 1}  = 0 \Leftrightarrow \sqrt {3x + 1}  =  - x - 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - x - 1 \ge 0}\\{3x + 1 = {{\left( { - x - 1} \right)}^2}}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le  - 1}\\{3x + 1 = {x^2} + 2x + 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le  - 1}\\{{x^2} - x = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \le  - 1}\\{\left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\end{array}} \right.}\end{array}} \right. \Leftrightarrow x \in \emptyset }\end{array}\)

Vậy hàm số có 1 TCN \(y = 0\) và 1 TCĐ \(x = 2\).

Chọn A.  

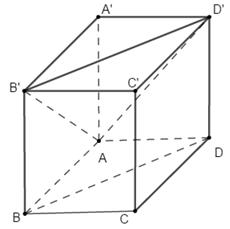
Đặt \(AD = a;{\mkern 1mu} {\mkern 1mu} AB = b;{\mkern 1mu} {\mkern 1mu} AA' = c.\)

Ta có diện tích hình chữ nhật ABCD, ABB'A', ADD'A' lần lượt là \(36c{m^2}\), \(225c{m^2}\), \(100c{m^2}\).

Suy ra \(\left\{ {\begin{array}{*{20}{l}}{ab = 36}\\{bc = 225}\\{ac = 100}\end{array}} \right. \Rightarrow {a^2}{b^2}{c^2} = 36.225.100 = 810000\) \( \Rightarrow abc = 900\).

Ta có: \({V_{A.A'B'D'}} = \dfrac{1}{3}.AA'.{S_{A'B'D'}} = \dfrac{1}{3}AA'.\dfrac{1}{2}{S_{A'B'C'D'}}.\)

\( \Rightarrow {V_{A.A'B'D'}} = \dfrac{1}{6}{V_{ABCD.A'B'C'D'}} = \dfrac{1}{6}.abc = 150{\mkern 1mu} {\mkern 1mu} \left( {c{m^3}} \right)\).

Chọn B.

Đồ thị hàm số \(y = \left| {f\left( x \right) - 2m} \right|\) có 5 điểm cực trị khi và chỉ khi đồ thị hàm số \(y = f\left( x \right)\) cắt trục hoành tại 3 điểm phân biệt \( \Leftrightarrow 4 - 2m < 0 < 11 - 2m \Leftrightarrow 4 < 2m < 11 \Leftrightarrow 2 < m < \dfrac{{11}}{2}\).

Chọn C.

Gọi phương trình đường thẳng bài cho là: \(d:{\mkern 1mu} {\mkern 1mu} y = ax + b.\)

Đường thẳng  \(d\) cắt đồ thị hàm số \(\left( C \right):{\mkern 1mu} {\mkern 1mu} y = {x^4} - 2{x^2}\) tại hai điểm có hoành độ là \((0;{\mkern 1mu} {\mkern 1mu} 1) \Rightarrow \) tọa độ hai điểm đó là: \(A\left( {0;{\mkern 1mu} 0} \right),{\mkern 1mu} {\mkern 1mu} B\left( {1; - 1} \right).\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a.0 + b = 0}\\{a + b = {\rm{\;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = 0}\\{a = {\rm{\;}} - 1}\end{array}} \right. \Rightarrow d:{\mkern 1mu} {\mkern 1mu} y = {\rm{\;}} - x.\)

Khi đó ta có phương trình hoành độ giao điểm của hai đồ thị hàm số là:

\(\begin{array}{*{20}{l}}{ - x = {x^4} - 2{x^2} \Leftrightarrow {x^4} - 2{x^2} + x = 0 \Leftrightarrow x\left( {{x^3} - 2x + 1} \right) = 0}\\{ \Leftrightarrow x\left( {x - 1} \right)\left( {{x^2} + x - 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\\{{x^2} + x - 1 = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}} \right.}\end{array}\)

Khi đó \(m,{\mkern 1mu} {\mkern 1mu} n\) là hai nghiệm của phương trình \(\left( * \right).\)

Áp dụng hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{m + n = {\rm{\;}} - 1}\\{mn = {\rm{\;}} - 1}\end{array}} \right..\)

\( \Rightarrow S = {m^2} + {n^2} = {\left( {m + n} \right)^2} - 2mn = 1 + 2 = 3.\)

Chọn D.

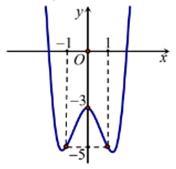
Số nghiệm của phương trình đã cho là số giao điểm của đồ thị hàm số \(y = {x^4} - 3{x^2} - 3\) và đường thẳng \(y = m.\)

Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = m\)  cắt đồ thị hàm số \(y = {x^4} - 3{x^2} - 3\) tại 3 điểm phân biệt \( \Leftrightarrow m = {\rm{\;}} - 3.\)

Chọn B.

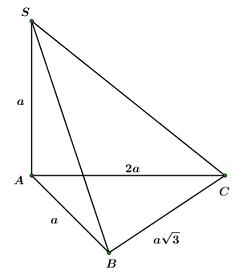
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AB = a \Rightarrow A{B^2} = {a^2}}\\{AC = 2a \Rightarrow A{C^2} = 4{a^2}}\\{BC = a\sqrt 3 {\rm{\;}} \Rightarrow B{C^2} = 3{a^2}}\end{array}} \right. \Rightarrow A{B^2} + B{C^2} = A{C^2}\)

\( \Rightarrow \Delta ABC\) vuông tại \(B\) (định lý Pitago đảo)

\(\begin{array}{*{20}{l}}{ \Rightarrow {S_{ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}.a.a\sqrt 3 {\rm{\;}} = \dfrac{{{a^2}\sqrt 3 }}{2}.}\\{ \Rightarrow {V_{SABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{6}.}\end{array}\)

Chọn B

TXĐ: \(D = \left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\).

Ta có

\(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } \dfrac{x}{{\sqrt {{x^2} - 1} }} = 1 \Rightarrow y = 1\) là tiệm cận  ngang của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } \dfrac{x}{{\sqrt {{x^2} - 1} }} =  - 1 \Rightarrow y = {\rm{\;}} - 1\) là tiệm cận ngang của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to \left( { - 1} \right)} \dfrac{x}{{\sqrt {{x^2} - 1} }} = \infty {\rm{\;}} \Rightarrow x = {\rm{\;}} - 1\) là tiệm cận đứng của đồ thị hàm số.

\(\mathop {\lim }\limits_{x \to 1} \dfrac{x}{{\sqrt {{x^2} - 1} }} = \infty {\rm{\;}} \Rightarrow x = 1\) là tiệm cận đứng của đồ thị hàm số.

Vậy đồ thị hàm số có tất cả 4 đường tiệm cận.

Chọn A.

Giả sử hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left( {a;{\mkern 1mu} {\mkern 1mu} b} \right)\) và chứa \({x_0} \in \left( {a;{\mkern 1mu} {\mkern 1mu} b} \right)\) thỏa mãn  \(f'\left( {{x_0}} \right) = 0\) và có đạo hàm cấp hai khác \(0\) tại điểm \({x_0}\) thì:

+) Hàm số đạt cực đại tại \({x_0}\) khi \(f''\left( {{x_0}} \right) < 0.\)

+) Hàm số đạt cực tiểu tại \({x_0}\) khi \(f''\left( {{x_0}} \right) > 0.\)

\( \Rightarrow \) khẳng định i) và ii) sai.

Khi \(f''\left( {{x_0}} \right) = 0\) ta không kết luận về cực trị của hàm số.

\( \Rightarrow \) khẳng định iii) sai.

Chọn A.

Đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x + 2}}\)có TCĐ: \(x = {\rm{\;}} - 2\), TCN: \(y = 2\)

\( \Rightarrow \)Tọa độ tâm I  là tâm đối xứng của đồ thị hàm số trên là: \(I\left( { - 2;2} \right)\).

Chọn A.

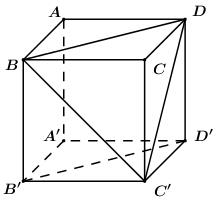
Do \(BD\parallel B'D'\) nên \(\angle \left( {BC';B'D'} \right) = \angle \left( {BC';BD} \right)\).

Giả sử cạnh của hình lập phương bằng 1. Áp dụng định lí Pytago trong các tam giác vuông ta có: \(BC' = BD = C'D = \sqrt 2 \).

Suy ra tam giác BC'D đều \( \Rightarrow \angle C'BD = {60^0}\).

Vậy \(\angle \left( {BC';B'D'} \right) = {60^0}\).

Chọn C.

\(f\left( x \right) = 2{x^3} + 3{x^2} - 1 \Rightarrow f'\left( x \right) = 6{x^2} + 6x\); \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\\{x = {\rm{\;}} - 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\end{array}} \right.\)

Hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 2; - \dfrac{1}{2}} \right]\), có \(f\left( { - 2} \right) =  - 5;f\left( { - 1} \right) = 0;f\left( { - \dfrac{1}{2}} \right) = {\rm{\;}} - \dfrac{1}{2}\)

\( \Rightarrow m = \mathop {\min }\limits_{\left[ { - 2; - \dfrac{1}{2}} \right]} f\left( x \right) = {\rm{\;}} - 5;{\mkern 1mu} {\mkern 1mu} M = \mathop {\max }\limits_{\left[ { - 2; - \dfrac{1}{2}} \right]} f\left( x \right) = 0\)\( \Rightarrow P = M - m = 5\).

Chọn C.

Khối đa diện đều loại \(\left\{ {5;3} \right\} \Rightarrow n = 5;{\mkern 1mu} {\mkern 1mu} p = 3\)

\( \Rightarrow 3D = 2C = 5M \Rightarrow M\) chia hết cho 6

Khi \(M = 6\) thì khối đa diện đều là khối lập phương thuộc loại \(\left\{ {4;3} \right\}\) (ktm).

Vậy \(M = 12\).

Chọn A.

Ta có : \(f'\left( x \right) = {\rm{\;}} - \left( {x - 10} \right){\left( {x - 11} \right)^2}{\left( {x - 12} \right)^{2019}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 10}\\{x = 11}\\{x = 12}\end{array}} \right.\)

BBT : 

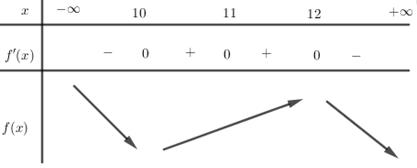
Từ BBT ta thấy hàm số đồng biến trên khoảng \(\left( {10;12} \right)\) nên C đúng.

Hàm số có 2 điểm cực trị.

Chọn C.

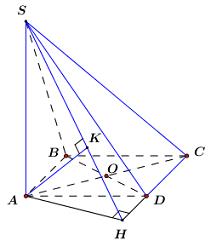
Ta có \(AB\parallel CD{\mkern 1mu} {\mkern 1mu} \left( {gt} \right) \Rightarrow AB\parallel \left( {SCD} \right)\) \( \Rightarrow d\left( {B;\left( {SCD} \right)} \right) = d\left( {A;\left( {SCD} \right)} \right)\).

Trong \(\left( {ABCD} \right)\) kẻ \(AH \bot CD\).

Vì \(\angle BAD = {60^0} \Rightarrow \angle ADC = {120^0}\) nên điểm \(H\) nằm ngoài đoạn thẳng CD.

Trong \(\left( {SAH} \right)\) dựng \(AK \bot SH{\mkern 1mu} {\mkern 1mu} \left( {H \in SH} \right)\) ta có:

\(\left\{ {\begin{array}{*{20}{l}}{CD \bot AH}\\{CD \bot SA{\mkern 1mu} {\mkern 1mu} \left( {SA \bot \left( {ABCD} \right)} \right)}\end{array}} \right.\) \( \Rightarrow CD \bot \left( {SAH} \right) \Rightarrow CD \bot AK\).

\(\left\{ {\begin{array}{*{20}{l}}{AK \bot SH}\\{AK \bot CD}\end{array}} \right. \Rightarrow AK \bot \left( {SCD} \right)\)\( \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AK\).

Xét tam giác vuông AHD có \(\angle ADH = {180^0} - \angle ADC = {60^0}\), \(AD = a\) \( \Rightarrow AH = AD.sin{60^0} = \dfrac{{a\sqrt 3 }}{2}\).

Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AH\), suy ra tam giác SAH vuông tại \(A\), áp dụng hệ thức lượng trong tam giác vuông ta có: \(AK = \dfrac{{SA.AH}}{{\sqrt {S{A^2} + A{H^2}} }}\) \( = \dfrac{{a.\dfrac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + \dfrac{{3{a^2}}}{4}} }} = \dfrac{{a\sqrt {21} }}{7}\).

Vậy \(d\left( {B;\left( {SCD} \right)} \right) = \dfrac{{a\sqrt {21} }}{7}\).

Chọn A.

TXĐ: \(\mathbb{R}\backslash \left\{ { - 1} \right\}\).

Ta có: \(y' = \dfrac{2}{{{{\left( { - 1 - x} \right)}^2}}} > 0{\mkern 1mu} {\mkern 1mu} \forall x \in D\).

Vậy hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\). Do đó hàm số đồng biến trên \(\left( {2; + \infty } \right)\).

Chọn D.

TXĐ: \(D = R\backslash \left\{ { = 3} \right\}\).

Ta có:

\(\begin{array}{*{20}{l}}{y' = \dfrac{{2x\left( {x + 3} \right) - {x^2} + 5}}{{{{\left( {x + 3} \right)}^2}}} = \dfrac{{{x^2} + 6x + 5}}{{{{\left( {x + 3} \right)}^2}}} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x =  - 1 \notin \left[ {0;2} \right]}\\{x =  - 5 \notin \left[ {0;2} \right]}\end{array}} \right.}\\{y\left( 0 \right) =  - \dfrac{5}{3};{\mkern 1mu} {\mkern 1mu} y\left( 2 \right) =  - \dfrac{1}{5}}\\{ \Rightarrow \mathop {\min }\limits_{x \in \left[ {0;2} \right]} y = \dfrac{{ - 5}}{3}}\end{array}\)

Chọn A.

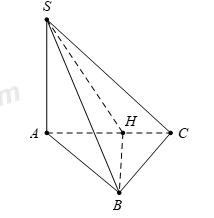
Kẻ \(BH \bot AC{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {H \in AC} \right)\)\( \Rightarrow {\mkern 1mu} {\mkern 1mu} BH \bot \left( {SAC} \right)\)

Suy ra \(\widehat {SB;\left( {SAC} \right)} = \widehat {\left( {SB;SH} \right)} = \widehat {BSH}.\)

Tam giác ABH vuông tại H, có \(\sin \widehat {BAH} = \dfrac{{BH}}{{AB}} \Rightarrow BH = a\sqrt 3 .\)

Tam giác SAB vuông tại A, có \(SB = \sqrt {S{A^2} + A{B^2}}  = a\sqrt 6 .\)

Do đó \(SB = \sqrt 2 {\mkern 1mu} BH{\mkern 1mu} {\mkern 1mu}  \Rightarrow {\mkern 1mu} {\mkern 1mu} \Delta {\mkern 1mu} ABH\) vuông cân tại \(H{\mkern 1mu} {\mkern 1mu}  \Rightarrow {\mkern 1mu} {\mkern 1mu} \widehat {BSH} = {45^0}.\)

Chọn B.