Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiCho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là một hình thoi cạnh a, \(\widehat {ABC} = {120^0}\); \(AA' = 4a\) Tính khoảng cách giữa hai đường thẳng A’C và BB’?
A. \(\dfrac{{a\sqrt 3 }}{2}\)
B. \(a\sqrt 3 \)
C. \(\dfrac{a}{2}\)
D. \(\dfrac{a}{{\sqrt 3 }}\)
Lời giải của giáo viên
ToanVN.com
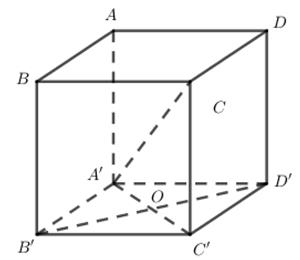
Ta có
\(\begin{array}{*{20}{l}}{\rm{\;}}&{BB'//CC' \Rightarrow BB'//\left( {ACC'} \right) \supset AC'}\\{\rm{\;}}&{ \Rightarrow d\left( {AC';BB'} \right) = d\left( {BB';\left( {ACC'} \right)} \right) = d\left( {B';\left( {ACC'} \right)} \right)}\end{array}\)
Gọi \(O = A'C' \cap B'D'\) ta có :
\(\left\{ {\begin{array}{*{20}{l}}{\rm{\;}}&{B'O \bot A'C'}\\{\rm{\;}}&{B'O \bot CC'}\end{array}} \right. \Rightarrow B'O \bot \left( {ACC'} \right) \Rightarrow d\left( {B';\left( {ACC'} \right)} \right) = B'O\)
Tam giác A’B’D’ là tam giác đều cạnh a
\( \Rightarrow B'D' = a \Rightarrow B'O = \dfrac{a}{2}\)
Chọn C.
CÂU HỎI CÙNG CHỦ ĐỀ
Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}}\) là:
Đồ thị hàm số \(y = \dfrac{x}{{\sqrt {{x^2} - 1} }}\) có bao nhiêu đường tiệm cận
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ
.jpg)
Hàm số đồng biến trên khoảng:
Khối lăng trụ có diện tích đáy bằng 4, chiều cao bằng 3 có thể tích bằng
Xét các khẳng định sau
i) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\)và đạt cực tiểu tại \(x = {x_0}\) thì \(\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) > 0}\end{array}} \right.\)
ii) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\)và đạt cực đại tại \(x = {x_0}\) thì \(\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) < 0}\end{array}} \right.\)
iii) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\) và \(f''({x_0}) = 0\)thì hàm số không đạt cực trị tại \(x = {x_0}\)
Số khẳng định đúng trong các khẳng định trên là
Có bao nhiêu điểm thuộc đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) thỏa mãn tiếp tuyến với đồ thị tại điểm đó có hệ số góc bằng 2018?
Số tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) song song với trục hoành là :
Thể tích V của khối chóp có diện tích đáy bằng B và chiều cao bằng h, được tính theo công thức
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), \(SA = a\), \(AB = a\), \(AC = 2a\), \(BC = a\sqrt 3 .\) Tính thể tích khối chóp S.ABC.
Tổng số mặt, số cạnh và số đỉnh của một hình lập phương là:
Cho hàm số \(y = f\left( x \right) = {x^2} - 2x + 3\). Mệnh đề nào sau đây đúng?
Cho hình chóp S.ABCD có đáy là hình thoi cạnh \(a\), \(\angle BAD = {60^0}\), cạnh bên \(SA = a\) và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
Một đường thẳng cắt đồ thị hàm số \(y = {x^4} - 2{x^2}\) tại 4 điểm phân biệt có hoành độ \(0,{\mkern 1mu} 1,{\mkern 1mu} m\) và n. Tính \(S = {m^2} + {n^2}.\)
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào?
.PNG)
Khối đa diện đều loại \(\left\{ {5;3} \right\}\) có bao nhiêu mặt?
