Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Phương trình trục hoành: \(y = 0\).
Ta có \(y' = 4{x^3} - 4x \Rightarrow \) Hệ số góc của tiếp tuyến tại điểm có hoành độ \(x = {x_0}\) là \(y'\left( {{x_0}} \right) = 4x_0^3 - 4{x_0}\).
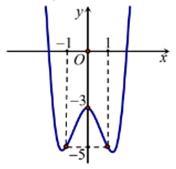
Tiếp tuyến // Ox \( \Rightarrow y'\left( {{x_0}} \right) = 0 \Leftrightarrow 4x_0^3 - 4{x_0} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x_0} = 0}\\{{x_0} = {\rm{\;}} \pm 1}\end{array}} \right.\).
Khi \(x = \pm 1\) ta tìm được hai tiếp tuyến trùng nhau là \(y = - 3\)
Vậy có hai tiếp tuyến song song với trục hoành.
Chọn C.
CÂU HỎI CÙNG CHỦ ĐỀ
Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}}\) là:
Khối lăng trụ có diện tích đáy bằng 4, chiều cao bằng 3 có thể tích bằng
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ
.jpg)
Hàm số đồng biến trên khoảng:
Đồ thị hàm số \(y = \dfrac{x}{{\sqrt {{x^2} - 1} }}\) có bao nhiêu đường tiệm cận
Cho hàm số \(y = f\left( x \right) = {x^2} - 2x + 3\). Mệnh đề nào sau đây đúng?
Thể tích V của khối chóp có diện tích đáy bằng B và chiều cao bằng h, được tính theo công thức
Xét các khẳng định sau
i) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\)và đạt cực tiểu tại \(x = {x_0}\) thì \(\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) > 0}\end{array}} \right.\)
ii) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\)và đạt cực đại tại \(x = {x_0}\) thì \(\left\{ {\begin{array}{*{20}{l}}{f'({x_0}) = 0}\\{f''({x_0}) < 0}\end{array}} \right.\)
iii) Nếu hàm số \(y = f\left( x \right)\) có đạo hàm cấp hai trên \(\mathbb{R}\) và \(f''({x_0}) = 0\)thì hàm số không đạt cực trị tại \(x = {x_0}\)
Số khẳng định đúng trong các khẳng định trên là
Đường cong trong hình vẽ bên dưới là đồ thị của hàm số nào?
Tổng số mặt, số cạnh và số đỉnh của một hình lập phương là:
Khối đa diện đều loại \(\left\{ {5;3} \right\}\) có bao nhiêu mặt?
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), \(SA = a\), \(AB = a\), \(AC = 2a\), \(BC = a\sqrt 3 .\) Tính thể tích khối chóp S.ABC.
Có bao nhiêu điểm thuộc đồ thị hàm số \(y = \dfrac{{2x - 1}}{{x - 1}}\) thỏa mãn tiếp tuyến với đồ thị tại điểm đó có hệ số góc bằng 2018?
Một đường thẳng cắt đồ thị hàm số \(y = {x^4} - 2{x^2}\) tại 4 điểm phân biệt có hoành độ \(0,{\mkern 1mu} 1,{\mkern 1mu} m\) và n. Tính \(S = {m^2} + {n^2}.\)
Cho hình chóp S.ABCD có đáy là hình thoi cạnh \(a\), \(\angle BAD = {60^0}\), cạnh bên \(SA = a\) và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
Đồ thị sau đây là của hàm số \(y = {x^4} - 3{x^2} - 3.\) Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} - 3 = m\) có đúng 3 nghiệm phân biệt.

.PNG)
