Trong không gian với hệ tọa độ Oxyz, cho điểm $M(1;2;3)$. Gọi $(P)$ là mặt phẳng đi qua điểm $M$ và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng $(P)$ cắt các trục tọa độ tại các điểm A,B,C . Tính thể tích khối chóp O.ABC.
A.
$\dfrac{{1372}}{9}.$
B.
$\dfrac{{686}}{9}.$
C.
$\dfrac{{524}}{3}.$
D.
$\dfrac{{343}}{9}.$
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
Ta có: .$d\left( {O;\left( P \right)} \right) \le OM$
Dấu bằng xảy ra $ \Leftrightarrow OM \bot \left( P \right) \Rightarrow \left( P \right)$ nhận $\overrightarrow {OM} = \left( {1;2;3} \right)$ là 1 VTPT. Do đó phương trình mặt phẳng (P) là: $1\left( {x - 1} \right) + 2\left( {y - 2} \right) + 3\left( {z - 3} \right) = 0\left( P \right):x + 2y + 3z - 14 = 0$
$ \Rightarrow A\left( {14;0;0} \right);B\left( {0;7;0} \right);C\left( {0;0;\dfrac{{14}}{3}} \right) \Rightarrow {V_{O.ABC}} = \dfrac{1}{6}OA.OB.OC = \dfrac{{686}}{9}.$
Hướng dẫn giải:
$d\left( {O;\left( P \right)} \right) \le OM$, để mặt phẳng (P) đi qua điểm M và cách O một khoảng lớn nhất thì (P) đi qua M và $\left( P \right) \bot OM$
Viết phương trình mặt phẳng (P), tìm tọa độ các điểm A, B, C và sử dụng công thức ${V_{OABC}} = \dfrac{1}{6}OA.OB.OC$
Ta có: .$d\left( {O;\left( P \right)} \right) \le OM$
Dấu bằng xảy ra $ \Leftrightarrow OM \bot \left( P \right) \Rightarrow \left( P \right)$ nhận $\overrightarrow {OM} = \left( {1;2;3} \right)$ là 1 VTPT. Do đó phương trình mặt phẳng (P) là: $1\left( {x - 1} \right) + 2\left( {y - 2} \right) + 3\left( {z - 3} \right) = 0\left( P \right):x + 2y + 3z - 14 = 0$
$ \Rightarrow A\left( {14;0;0} \right);B\left( {0;7;0} \right);C\left( {0;0;\dfrac{{14}}{3}} \right) \Rightarrow {V_{O.ABC}} = \dfrac{1}{6}OA.OB.OC = \dfrac{{686}}{9}.$
Hướng dẫn giải:
$d\left( {O;\left( P \right)} \right) \le OM$, để mặt phẳng (P) đi qua điểm M và cách O một khoảng lớn nhất thì (P) đi qua M và $\left( P \right) \bot OM$
Viết phương trình mặt phẳng (P), tìm tọa độ các điểm A, B, C và sử dụng công thức ${V_{OABC}} = \dfrac{1}{6}OA.OB.OC$
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số $y = f\left( x \right)$ xác định liên tục trên R có bảng biến thiên:
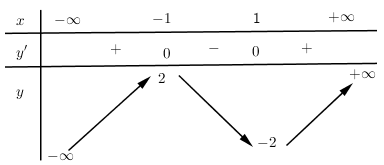
Khẳng định nào sau đây là đúng?
Cho hai hàm số $y = \dfrac{{2x - 1}}{{{m^2} - 8 - x}}$ và $y = \dfrac{{5 - 2x}}{{x + 4}}$. Tập hợp các giá trị của tham số $m$ để hai đường tiệm cận đứng của hai đồ thị hàm số trên trùng nhau là:
Độ dài đoạn thẳng \(AB\) với \(A\left( {2;1;0} \right),B\left( {4; - 1;1} \right)\) là một số:
Cho hai điểm \(M\left( {1; - 2; - 4} \right),M'\left( {5; - 4;2} \right)\). Biết \(M'\) là hình chiếu của \(M\) lên mặt phẳng \(\left( P \right)\). Khi đó, phương trình \(\left( P \right)\) là:
Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)
Cho số dương \(a\) thỏa mãn điều kiện hình phẳng giới hạn bởi các đường parabol \(y=a{{x}^{2}}-2\) và \(y=4-2a{{x}^{2}}\) có diện tích bằng $16$. Giá trị của \(a\) bằng
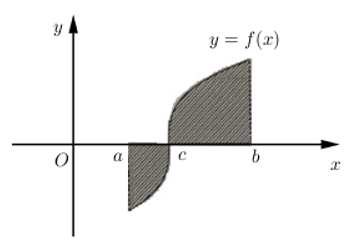
Cho hàm số \(y=f\left( x \right)\) liên tục trên đoạn \(\left[ a;b \right]\) và cắt trục hoành tại điểm \(x=c\,\,\left( a<c<b \right)\) (như hình vẽ bên) Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y=f\left( x \right)\), trục hoành và hai đường thẳng \(x=a;x=b\). Mệnh đề nào dưới đây đúng ?
Trong không gian với hệ tọa độ Oxyz, cho điểm \(M\) thỏa mãn hệ thức \(\overrightarrow {OM} = 2\overrightarrow i + \overrightarrow j \). Tọa độ của điểm \(M\) là:
Cho khối đa diện lồi có số đỉnh, số mặt và số cạnh lần lượt là \(D,M,C\). Chọn mệnh đề đúng:
Hình trụ có bán kính \(r = 5cm\) và chiều cao \(h = 3cm\) có diện tích toàn phần gần với số nào sau đây?
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
Trong không gian với hệ tọa độ \(Oxyz\), cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 2,{\rm{ }}\left| {\overrightarrow b } \right| = 5\) và \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {30^0}\). Độ dài của vectơ \(\left[ {\overrightarrow a ,\overrightarrow b } \right]\) bằng:
Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm \(y=\tan x\), trục \(Ox\), đường thẳng \(x=0\), đường thẳng \(x=\frac{\pi }{3}\) quanh trục \(Ox\) là
Một người vay ngân hàng một số tiền với lãi suất mỗi tháng là $1,12\% $. Biết cuối mỗi tháng người đó phải trả cho ngân hàng $3.000.000$ đồng và trả trong $1$ năm thì hết nợ. Số tiền người đó vay là:


