Kết quả tích phân \(I = \int\limits_1^e {\dfrac{{\ln x}}{{x\left( {{{\ln }^2}x + 1} \right)}}dx} \) có dạng \(I = a\ln 2 + b\) với \(a,b \in Q\) . Khẳng định nào sau đây là đúng?
A.
$2a + b = 1$
B.
\({a^2} + {b^2} = 4\)
C.
\(a - b = 1\)
D.
\(ab = \dfrac{1}{2}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Cách 1: Đặt \(t = {\ln ^2}x + 1 \Rightarrow dt = 2\ln x\dfrac{{dx}}{x} \Rightarrow \dfrac{{\ln xdx}}{x} = \dfrac{{dt}}{2}\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 1\\x = e \Rightarrow t = 2\end{array} \right.\)
Khi đó ta có:
\(I = \dfrac{1}{2}\int\limits_1^2 {\dfrac{{dt}}{t}} = \left. {\dfrac{1}{2}\ln \left| t \right|} \right|_1^2 = \dfrac{1}{2}\ln 2 = a\ln 2 + b \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = 0\end{array} \right. \Rightarrow 2a + b = 1\)
Hướng dẫn giải:
- Bước 1: Đặt \(t = u\left( x \right)\), đổi cận \(\left\{ \begin{array}{l}x = a \Rightarrow t = u\left( a \right) = a'\\x = b \Rightarrow t = u\left( b \right) = b'\end{array} \right.\) .
- Bước 2: Tính vi phân \(dt = u'\left( x \right)dx\).
- Bước 3: Biến đổi \(f\left( x \right)dx\) thành \(g\left( t \right)dt\).
- Bước 4: Tính tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_{a'}^{b'} {g\left( t \right)dt} \).
Giải thích thêm:
Một số em khi tính được \(a = \dfrac{1}{2},b = 0\) thì vội vàng kết luận \(ab = \dfrac{1}{2}\) và chọn D là sai.
Cách 2: Dùng MTCT tính tích phân $I$ sau đó dùng [SHIFT] [STO] gán giá trị vừa nhận được cho biến A.
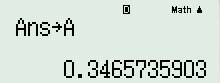
Khi đó ta có: \(A = a\ln 2 + b \Rightarrow b = A - a\ln 2\)
Coi $a$ là biến $x$ khi đó \(b = f\left( x \right) = A - x\ln 2\)
Sử dụng [MODE] [7] cho $x$ chạy từ -2 đến 2, step là 0,5, khi $x$ và $f(x)$ cùng đẹp đó chính là giá trị cần tìm.
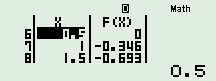
Ta thấy khi $x = 0,5$ thì $f(x) = 0$ hay khi $a = 0,5$ thì $b = 0$. Do đó $2a + b = 1$.
Cách 1: Đặt \(t = {\ln ^2}x + 1 \Rightarrow dt = 2\ln x\dfrac{{dx}}{x} \Rightarrow \dfrac{{\ln xdx}}{x} = \dfrac{{dt}}{2}\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 1\\x = e \Rightarrow t = 2\end{array} \right.\)
Khi đó ta có:
\(I = \dfrac{1}{2}\int\limits_1^2 {\dfrac{{dt}}{t}} = \left. {\dfrac{1}{2}\ln \left| t \right|} \right|_1^2 = \dfrac{1}{2}\ln 2 = a\ln 2 + b \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = 0\end{array} \right. \Rightarrow 2a + b = 1\)
Hướng dẫn giải:
- Bước 1: Đặt \(t = u\left( x \right)\), đổi cận \(\left\{ \begin{array}{l}x = a \Rightarrow t = u\left( a \right) = a'\\x = b \Rightarrow t = u\left( b \right) = b'\end{array} \right.\) .
- Bước 2: Tính vi phân \(dt = u'\left( x \right)dx\).
- Bước 3: Biến đổi \(f\left( x \right)dx\) thành \(g\left( t \right)dt\).
- Bước 4: Tính tích phân \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_{a'}^{b'} {g\left( t \right)dt} \).
Giải thích thêm:
Một số em khi tính được \(a = \dfrac{1}{2},b = 0\) thì vội vàng kết luận \(ab = \dfrac{1}{2}\) và chọn D là sai.
Cách 2: Dùng MTCT tính tích phân $I$ sau đó dùng [SHIFT] [STO] gán giá trị vừa nhận được cho biến A.
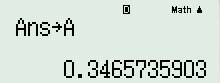
Khi đó ta có: \(A = a\ln 2 + b \Rightarrow b = A - a\ln 2\)
Coi $a$ là biến $x$ khi đó \(b = f\left( x \right) = A - x\ln 2\)
Sử dụng [MODE] [7] cho $x$ chạy từ -2 đến 2, step là 0,5, khi $x$ và $f(x)$ cùng đẹp đó chính là giá trị cần tìm.
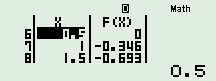
Ta thấy khi $x = 0,5$ thì $f(x) = 0$ hay khi $a = 0,5$ thì $b = 0$. Do đó $2a + b = 1$.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho vật thể \(V\) được giới hạn bởi hai mặt phẳng \(x = 0\) và \(x = - 2\), mặt phẳng vuông góc với trục \(Ox\) cắt \(V\) theo thiết diện \(S\left( x \right) = 2{x^2}\). Thể tích của \(V\) được tính bởi:
Cho \(f\left( x \right) = \dfrac{{{x^2}}}{{\sqrt {1 - x} }}\) và \(\int {f\left( x \right)dx = - 2\int {{{\left( {{t^2} - m} \right)}^2}dt} } \) với \(t = \sqrt {1 - x} \) , giá trị của $m$ bằng ?
Hàm số $y = \sin x$ là một nguyên hàm của hàm số nào trong các hàm số sau?
Giả sử rằng \(\int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\tan xdx}}{{1 + {{\cos }^2}x}}} = m\ln \dfrac{3}{2}\). Tìm giá trị của m.
Cho hàm số \(y=f(x)={{x}^{3}}-3{{x}^{2}}-4x\,\,(C)\). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số (C) và trục hoành. Phát biểu nào sau đây đúng?
Cho hàm số $f\left( x \right)$ thỏa mãn $f'\left( x \right){\left[ {f\left( x \right)} \right]^{2018}} = x.{e^x}{\mkern 1mu} {\mkern 1mu} \forall x \in R$ và $f\left( 1 \right) = 1$. Hỏi phương trình $f\left( x \right) = - \dfrac{1}{e}$ có bao nhiêu nghiệm?
Thể tích vật thể nằm giữa hai mặt phẳng \(x=0\) và \(x=2\), biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \(\left( 0\le x\le 2 \right)\) là một nửa đường tròn đường kính \(\sqrt{5}{{x}^{2}}\) bằng :
Biết rằng$\int {{e^{2x}}\cos 3xdx = {e^{2x}}\left( {a\cos 3x + b\sin 3x} \right) + c} $, trong đó $a, b, c$ là các hằng số, khi đó tổng $a + b$ có giá trị là:
Nếu đặt $\left\{ \begin{array}{l}u = \ln \left( {x + 2} \right)\\{\rm{d}}v = x\,{\rm{d}}x\end{array} \right.$ thì tích phân $I = \int\limits_0^1 {x.\ln \left( {x + 2} \right){\rm{d}}x} $ trở thành
Trong không gian với hệ tọa độ \(Oxyz,\) cho mặt phẳng \(\left( P \right):y-2z+1=0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)\) ?
Trong không gian với hệ tọa độ Oxyz, cho ba vector $\vec a = \left( {2;3; - 5} \right);{\mkern 1mu} {\mkern 1mu} \vec b = \left( {0; - 3;4} \right);{\mkern 1mu} {\mkern 1mu} \vec c = \left( {1; - 2;3} \right)$. Tọa độ vector $\vec n = 3\vec a + 2\vec b - \vec c$ là:
Trong không gian \(Oxyz\) cho điểm \(M\left( {2;1;5} \right)\). Mặt phẳng \((P)\) đi qua điểm \(M\) và cắt các trục \(Ox,Oy,Oz\) lần lượt tại các điểm \(A,B,C\) sao cho \(M\) là trực tâm của tam giác \(ABC.\) Tính khoảng cách từ điểm \(I\left( {1;2;3} \right)\) đến mặt phẳng \((P)\).
Cô sin của góc hợp bởi hai véc tơ \(\overrightarrow {{u_1}} \left( {{x_1};{y_1};{z_1}} \right)\) và \(\overrightarrow {{u_2}} \left( {{x_2};{y_2};{z_2}} \right)\) là:
Gọi $F(x)$ là một nguyên hàm của hàm số \(f\left( x \right)=-\dfrac{1}{{{\cos }^{2}}x}\) thỏa mãn \(F\left( 0 \right)=1\). Tìm $F(x).$
Cho tích phân $I = \int\limits_{\dfrac{\pi }{4}}^{\dfrac{\pi }{2}} {\dfrac{{\ln \left( {3\sin x + \cos x} \right)}}{{{{\sin }^2}x}}{\rm{d}}x} = m.\ln \sqrt 2 + n.\ln 3 - \dfrac{\pi }{4}$, tổng $m + n$

