Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
\(f\left( x \right)=2x+\sin 2x \) \(\Rightarrow F\left( x \right)=\int{f\left( x \right)dx}=\int{\left( 2x+\sin 2x \right)dx}\) \(={{x}^{2}}-\dfrac{1}{2}\cos 2x+C\)
Giải thích thêm:
\(\left( \sin kx \right)'=k\cos kx,\,\,\int{\sin kxdx}=-\dfrac{1}{k}\cos kx+C\)
\(f\left( x \right)=2x+\sin 2x \) \(\Rightarrow F\left( x \right)=\int{f\left( x \right)dx}=\int{\left( 2x+\sin 2x \right)dx}\) \(={{x}^{2}}-\dfrac{1}{2}\cos 2x+C\)
Giải thích thêm:
\(\left( \sin kx \right)'=k\cos kx,\,\,\int{\sin kxdx}=-\dfrac{1}{k}\cos kx+C\)
CÂU HỎI CÙNG CHỦ ĐỀ
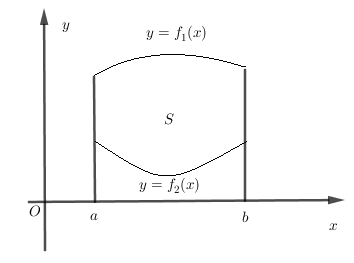
Cho hai hàm số \(y = {f_1}\left( x \right)\) và \(y = {f_2}\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và có đồ thị như hình vẽ bên. Gọi $S$ là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng \(x = a,x = b\). Thể tích $V$ của vật thể tròn xoay tạo thành khi quay $S$ quanh trục $Ox$ được tính bởi công thức nào sau đây ?
Cho nguyên hàm \(\int {x\sin xdx} \). Nếu đặt \(\left\{ \begin{array}{l}u = x\\dv = \sin xdx\end{array} \right.\) thì:
Diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = {x^3} - x;y = 2x$ và các đường thẳng $x = - 1;x = 1$ được xác định bởi công thức:
Cho hàm số \(y=f\left( x \right)\) liên tục và có đồ thị như hình bên. Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục \(Ox.\) Quay hình phẳng \(D\) quanh trục \(Ox\) ta được khối tròn xoay có thể tích \(V\) được xác định theo công thức
Cho hai hàm số \(f,\,\,g\) liên tục trên đoạn $\left[ {a;b} \right]$ và số thực $k$ tùy ý. Trong các khẳng định sau, khẳng định nào sai ?
Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=x{{e}^{x}},\ \ y=0,\ x=0,\ x=1\) xung quanh trục \(Ox\) là:
Cho hàm số $f\left( x \right)$ liên tục trên $R$ và $\int\limits_{ - 2}^4 {f\left( x \right)} dx{\rm{ = 2}}$ . Mệnh đề nào sau đây là sai?
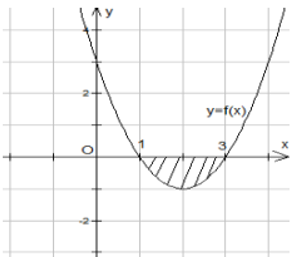
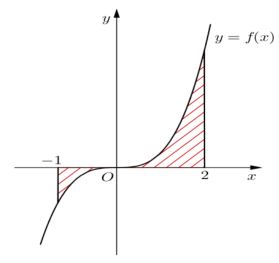
Gọi \(S\) là diện tích hình phẳng \(\left( H \right)\) giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng \(x = - 1,x = 2\) (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$ Mệnh đề nào sau đây đúng?
Tìm thể tích \(V\) của vật tròn xoay sinh ra bởi đường tròn \({{x}^{2}}+{{\left( y-3 \right)}^{2}}=4\) khi quay quanh trục \(Ox.\)
Biết \(F\left( x \right)\) là một nguyên hàm của hàm số\(f\left( x \right) = \dfrac{x}{{\sqrt {8 - {x^2}} }}\) thoả mãn \(F\left( 2 \right) = 0\). Khi đó phương trình \(F\left( x \right) = x\) có nghiệm là
Tích phân \(I = \int\limits_1^2 {{x^5}} dx\) có giá trị là:
Cho hàm số \(f\left( x \right) = {e^{ - 2018x + 2017}}\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f\left( x \right)\) mà \(F\left( 1 \right) = e\). Chọn mệnh đề đúng:
Biết $\int {f\left( x \right){\mkern 1mu} {\rm{d}}x = 2x\ln \left( {3x - 1} \right) + C} $ với $x \in \left( {\dfrac{1}{9}; + \infty } \right)$. Tìm khẳng định đúng trong các khẳng định sau.
Kết quả tích phân \(I = \int\limits_1^e {\dfrac{{\ln x}}{{x\left( {{{\ln }^2}x + 1} \right)}}dx} \) có dạng \(I = a\ln 2 + b\) với \(a,b \in Q\) . Khẳng định nào sau đây là đúng?

