Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: d
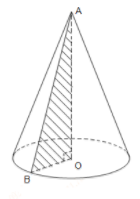
Quan sát hình vẽ ta thấy: \(l = AB,r = OB,h = AO\).
Mà \(A{B^2} = A{O^2} + O{B^2}\) nên \({l^2} = {r^2} + {h^2}\)
Hướng dẫn giải:
Sử dụng định lý Pi-ta-go cho tam giác vuông.
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án C vì biến đổi nhầm định lý Pi-ta-go.

Quan sát hình vẽ ta thấy: \(l = AB,r = OB,h = AO\).
Mà \(A{B^2} = A{O^2} + O{B^2}\) nên \({l^2} = {r^2} + {h^2}\)
Hướng dẫn giải:
Sử dụng định lý Pi-ta-go cho tam giác vuông.
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án C vì biến đổi nhầm định lý Pi-ta-go.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình nón có các kích thước \(r = 1;h = 2\) với \(r,h\) lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
Khối trụ tròn xoay có thể tích bằng \(144\pi \) và bán kính đáy bằng 6. Đường sinh của khối trụ bằng:
Điểm \(M\) thuộc mặt cầu tâm \(O\) bán kính \(R\) nếu:
Diện tích xung quanh của hình nón có bán kính đường tròn đáy \(R\) và chiều cao \(h\) bằng:
Cho mặt cầu \(\left( S \right)\) có đường kính 10 cm và mặt phẳng \(\left( P \right)\) cách tâm mặt cầu một khoảng 4 cm. Khẳng định nào sau đây sai?
Một khối trụ có bán kính đáy bằng \(2\), chiều cao bằng \(3\). Tính thể tích \(V\) của khối trụ.
Cho khối nón có độ dài đường sinh bằng \(2a\) và bán kính đáy bằng \(a\). Thể tích của khối nón đã cho bằng
Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại A với AB = AC = 2; \(\angle BAC = {120^0}\). Tính diện tích mặt cầu ngoại tiếp lăng trụ trên.
Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là \(12\,{\rm{cm}}\). Giá trị lớn nhất của thể tích khối trụ là
Hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$ có $SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$ và có $SA = a,AB = b,AC = c$. Mặt cầu đi qua các đỉnh $A,B,C,S$ có bán kính $r$ bằng :

