Cho \(x\), \(y\) là những số thực thoả mãn \({x^2} - xy + {y^2} = 1\). Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của \(P = \dfrac{{{x^4} + {y^4} + 1}}{{{x^2} + {y^2} + 1}}\). Giá trị của \(A = M + 15m\) là
A.
\(A = 17 - 2\sqrt 6 \).
B.
\(A = 17 + \sqrt 6 \).
C.
\(A = 17 + 2\sqrt 6 \).
D.
\(A = 17 - \sqrt 6 \).
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Ta có
+) \(1 + xy = {x^2} + {y^2} \ge 2xy \Leftrightarrow xy \le 1\) vì \({\left( {x - y} \right)^2} = {x^2} + {y^2} - 2xy \ge 0\).
+) \({x^2} - xy + {y^2} = 1 \Leftrightarrow {\left( {x + y} \right)^2} - 3xy = 1 \Leftrightarrow {\left( {x + y} \right)^2} = 1 + 3xy \ge 0 \Leftrightarrow xy \ge - \dfrac{1}{3}\).
Khi đó \(P = \dfrac{{{x^4} + {y^4} + 1}}{{{x^2} + {y^2} + 1}} = \dfrac{{{{\left( {{x^2} + {y^2}} \right)}^2} - 2{x^2}{y^2} + 1}}{{{x^2} + {y^2} + 1}} = \dfrac{{{{\left( {1 + xy} \right)}^2} - 2{{\left( {xy} \right)}^2} + 1}}{{xy + 2}}\).
Đặt \(t = xy,\,t \in \left[ { - \dfrac{1}{3};\,\,1} \right]\), xét hàm số \(P = \dfrac{{ - {t^2} + 2t + 2}}{{t + 2}}\)
\(P' = \dfrac{{ - {t^2} - 4t + 2}}{{{{\left( {t + 2} \right)}^2}}}\); \(P' = 0 \Leftrightarrow t = - 2 + \sqrt 6 \)
Mà \(P\left( { - \dfrac{1}{3}} \right) = \dfrac{{11}}{{15}}\); \(P\left( 1 \right) = 1\); \(P\left( { - 2 + \sqrt 6 } \right) = 6 - 2\sqrt 6 \)
Khi đó: \(m = P\left( { - \dfrac{1}{3}} \right) = \dfrac{{11}}{{15}}\); \(M = P\left( { - 2 + \sqrt 6 } \right) = 6 - 2\sqrt 6 \)
Vậy \(A = M + 15m = 17 - 2\sqrt 6 \).
Hướng dẫn giải:
- Tìm tập giá trị của tích \(xy\) dựa vào điều kiện bài cho.
- Biến đổi \(P\) chỉ làm xuất hiện tích \(xy\) rồi đặt \(t = xy\)
- Xét hàm số \(P\left( t \right)\) và tìm \(\max ,\min \), chú ý điều kiện của \(t\) tìm được từ đầu.
Ta có
+) \(1 + xy = {x^2} + {y^2} \ge 2xy \Leftrightarrow xy \le 1\) vì \({\left( {x - y} \right)^2} = {x^2} + {y^2} - 2xy \ge 0\).
+) \({x^2} - xy + {y^2} = 1 \Leftrightarrow {\left( {x + y} \right)^2} - 3xy = 1 \Leftrightarrow {\left( {x + y} \right)^2} = 1 + 3xy \ge 0 \Leftrightarrow xy \ge - \dfrac{1}{3}\).
Khi đó \(P = \dfrac{{{x^4} + {y^4} + 1}}{{{x^2} + {y^2} + 1}} = \dfrac{{{{\left( {{x^2} + {y^2}} \right)}^2} - 2{x^2}{y^2} + 1}}{{{x^2} + {y^2} + 1}} = \dfrac{{{{\left( {1 + xy} \right)}^2} - 2{{\left( {xy} \right)}^2} + 1}}{{xy + 2}}\).
Đặt \(t = xy,\,t \in \left[ { - \dfrac{1}{3};\,\,1} \right]\), xét hàm số \(P = \dfrac{{ - {t^2} + 2t + 2}}{{t + 2}}\)
\(P' = \dfrac{{ - {t^2} - 4t + 2}}{{{{\left( {t + 2} \right)}^2}}}\); \(P' = 0 \Leftrightarrow t = - 2 + \sqrt 6 \)
Mà \(P\left( { - \dfrac{1}{3}} \right) = \dfrac{{11}}{{15}}\); \(P\left( 1 \right) = 1\); \(P\left( { - 2 + \sqrt 6 } \right) = 6 - 2\sqrt 6 \)
Khi đó: \(m = P\left( { - \dfrac{1}{3}} \right) = \dfrac{{11}}{{15}}\); \(M = P\left( { - 2 + \sqrt 6 } \right) = 6 - 2\sqrt 6 \)
Vậy \(A = M + 15m = 17 - 2\sqrt 6 \).
Hướng dẫn giải:
- Tìm tập giá trị của tích \(xy\) dựa vào điều kiện bài cho.
- Biến đổi \(P\) chỉ làm xuất hiện tích \(xy\) rồi đặt \(t = xy\)
- Xét hàm số \(P\left( t \right)\) và tìm \(\max ,\min \), chú ý điều kiện của \(t\) tìm được từ đầu.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy $ABCD$ là hình vuông cạnh bằng $a$. Hình chiếu vuông góc của điểm $A'$ trên mặt phẳng $\left( {ABCD} \right)$ là trung điểm $I$ của cạnh $AB$. Biết \(A'C\) tạo với mặt phẳng đáy một góc \(\alpha \) với \(\tan \alpha = \dfrac{2}{{\sqrt 5 }}\). Thể tích khối chóp $A'.ICD$ là:
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
Hàm số $y = {x^3} + 2a{x^2} + 4bx - 2018,{\mkern 1mu} {\mkern 1mu} (a,{\mkern 1mu} b \in R)$ đạt cực trị tại $x = - 1$ . Khi đó hiệu $a - b$ là:
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(C,\)\(AB = a\sqrt 5 ,\)\(AC = a.\) Cạnh bên \(SA = 3a\) và vuông góc với mặt phẳng đáy. Thể tích của khối chóp \(S.ABC\) bằng
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Tính thể tích khối chóp \(S.ABC\).
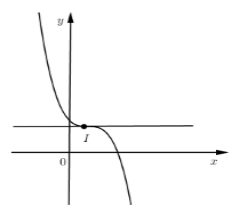
Hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ, chọn kết luận đúng:
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, \(SA \bot (ABCD)\) và \(SA = a\sqrt 6 \). Thể tích của khối chóp $S.ABCD$ bằng
Khối đa diện đều nào sau đây có các mặt không phải là tam giác đều

Vật thể nào trong các vật thể sau không phải là khối đa diện?

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là
Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình bên. Số điểm cực trị của hàm số đã cho là:
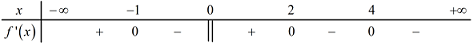
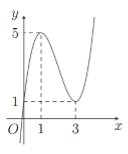
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right) = 3\) là:
Một nhà máy cần thiết kế một chiếc bể đựng nước hình trụ bằng tôn có nắp, có thể tích là \(64\pi \left( {{m^3}} \right)\). Tìm bán kính đáy \(r\) của hình trụ sao cho hình trụ được làm ra tốn ít nhiên liệu nhất.
Cho khối chóp \(S.ABC\). Trên các cạnh \(SA,SB,SC\) lấy các điểm \(A',B',C'\) sao cho \(A'A = 2SA',B'B = 2SB',C'C = 2SC'\), khi đó tồn tại một phép vị tự biến khối chóp \(S.ABC\) thành khối chóp \(S.A'B'C'\) với tỉ số đồng dạng là:

