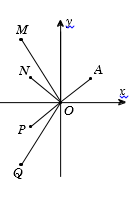
Cho số phức \(z\) thỏa mãn \(\left| z \right| = 1\) và điểm \(A\) trong hình vẽ bên là điểm biểu diễn của \(z\). Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức $w = \dfrac{1}{{iz}}$ là một trong bốn điểm \(M,{\rm{ }}N,{\rm{ }}P,{\rm{ }}Q\). Khi đó điểm biểu diễn của số phức $w$ là

Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đồ thị $y =  - \,\sqrt {4 - {x^2}} ,\,\,{x^2} + 3y = 0$ quay quanh trục $Ox$ là $V = \dfrac{{a\pi \sqrt 3 }}{b},$ với $a,\,\,b > 0$ và $\dfrac{a}{b}$ là phân số tối giản. Tính tổng $T = a + b.$

Cho hình phẳng $\left( H \right)$ giới hạn bởi \(y = \dfrac{1}{3}{x^3} - {x^2}\) và $Ox$.  Thể tích khối tròn xoay sinh ra khi quay $\left( H \right)$  quanh $Ox$ bằng :

Trong các tích phân sau, tích phân nào có giá trị bằng \(2\)?

Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(d:\dfrac{{x - 3}}{1} = \dfrac{{y - 3}}{3} = \dfrac{z}{2}\), mặt phẳng \(\left( \alpha  \right):x + y - z + 3 = 0\) và điểm \(A\left( {1;2 - 1} \right)\). Đường thẳng \(\Delta \) đi qua \(A\) cắt \(d\) và song song với mặt phẳng \(\left( \alpha  \right)\) có phương trình là:

Trong các khẳng định sau, khẳng định nào sai ?

Cho tam giác \(ABC\) có \(A\left( {0;0;1} \right)\), \(B\left( {0; - 1;0} \right)\) và \(C\left( {2;1; - 2} \right)\). Gọi \(G\) là trọng tâm tam giác. Phương trình đường thẳng \(AG\) là:

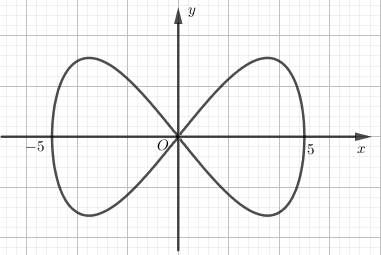
Trong Công viên Toán học có những mảnh đất hình dáng khác nhau. Mỗi mảnh được trồng một loài hoa và nó được tạo thành bởi một trong những đường cong đẹp nhất trong toán học. Ở đó có mảnh đất mang tên Bernoulli, nó được tạo thành từ đường Lemniscate có phương trình trong hệ tọa độ $Oxy$ là \(16{y^2} = {x^2}\left( {25 - {x^2}} \right)\) như hình vẽ bên. Tính diện tích $S$ của mảnh đất Bernoulli biết rằng mỗi đơn vị trong hệ trục tọa độ $Oxy$ tương ứng với chiều dài $1$ mét

Viết phương trình mặt phẳng $\left( P \right)$  đi qua điểm $M\left( {1;0; - 2} \right)$ và vuông góc với hai mặt phẳng $\left( Q \right),\left( R \right)$  cho trước với $\left( Q \right):x + 2y - 3z + 1 = 0$  và $\left( {{\rm{ }}R} \right):2x - 3y + z + 1 = 0$ .

Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(A\left( {1;0;2} \right)\) và đường thẳng \(d:\dfrac{{x - 1}}{1} = \dfrac{y}{1} = \dfrac{{z + 1}}{2}\). Viết phương trình đường thẳng \(\Delta \) đi qua \(A,\) vuông góc và cắt \(d\).

 Với cách đổi biến \(u=\sqrt{1+3\ln x}\) thì tích phân \(\int\limits_{1}^{e}{\frac{\ln x}{x\sqrt{1+3\ln x}}}dx\) trở thành: 

Cho số phức $z$ thỏa mãn $\left| {z - 2} \right| = 2$. Biết rằng tập hợp các điểm biểu diễn các số phức $w = \left( {1 - i} \right)z + i$ là một đường tròn. Tính bán kính $r$ của đường tròn đó

Cho $F\left( x \right) = {x^2}$ là nguyên hàm của hàm số $f\left( x \right){e^{2x}}$ và $f\left( x \right)$ là hàm số thỏa mãn điều kiện $f\left( 0 \right) =  0,\,\,f\left( 1 \right) = \dfrac{2}{e^2}.$ Tính tích phân $I = \int\limits_0^1 {f'\left( x \right){e^{2x}}{\rm{d}}x} .$

Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right)={{x}^{2}}+2x-3\) thỏa mãn \(F\left( 0 \right)=4,\) giá trị của \(F\left( 1 \right)\) bằng

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm

$A\left( {1;2; - 1} \right),{\rm{ }}B\left( {2;1;1} \right),{\rm{ }}C\left( {0;1;2} \right)$. Gọi $H\left( {a;b;c} \right)$ là trực tâm của tam giác \(ABC\). Giá trị của $a + b + c$ bằng:

 Trong không gian với hệ tọa độ \(Oxyz,\) cho hai mặt phẳng \(\left( P \right):3x+y+z-5=0\) và \(\left( Q \right):x+2y+z-4=0.\) Khi đó, giao tuyến của \(\left( P \right)\) và \(\left( Q \right)\) có phương trình là