Lý Thuyết Lớp 12
Lý thuyết lớp 11
Lý thuyết lớp 10
Lý thuyết lớp 9
Lý thuyết lớp 8
Lý thuyết lớp 7
Lý thuyết lớp 6
Lý thuyết lớp 5
Lý thuyết lớp 4
Lý thuyết lớp 3
Lý thuyết lớp 2
Lý thuyết lớp 1
Thi vào lớp 10
Đại học
Thư viện câu hỏi
Thi Online
Hỏi bàiCho phương trình \(m\ln \left( {x + 1} \right) - x - 2 = 0\). Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(0 < {x_1} < 2 < 4 < {x_2}\) là khoảng \(\left( {a; + \infty } \right).\) Khi đó \(a\) thuộc khoảng nào dưới đây ?
A.
\(\left( {3,7;3,8} \right).\)
B.
\(\left( {3,6;3,7} \right).\)
C.
\(\left( {3,8;3,9} \right).\)
D.
\(\left( {3,5;3,6} \right).\)
Lời giải của giáo viên
ToanVN.com
Đáp án đúng: a
ĐKXĐ: \(x > - 1\).
Ta có: \(m\ln \left( {x + 1} \right) - x - 2 = 0 \Leftrightarrow m\ln \left( {x + 1} \right) = x + 2\) (1)
Dễ dàng kiểm tra \(x = 0\) không phải nghiệm của phương trình trên.
Với \(x \ne 0\), phương trình \(\left( 1 \right) \Leftrightarrow m = \dfrac{{x + 2}}{{\ln \left( {x + 1} \right)}}\)
Xét hàm số \(f\left( x \right) = \dfrac{{x + 2}}{{\ln \left( {x + 1} \right)}}\,\,\left( {x > - 1,\,\,x \ne 0} \right)\) ta có: \(f'\left( x \right) = \dfrac{{\ln \left( {x + 1} \right) - \dfrac{{x + 2}}{{x + 1}}}}{{{{\ln }^2}\left( {x + 1} \right)}}\)
Nhận xét: Trên \(\left( { - 1; + \infty } \right)\backslash \left\{ 0 \right\}\), hàm số \(y = \ln (x + 1)\) đồng biến, hàm số \(y = \dfrac{{x + 2}}{{x + 1}}\) nghịch biến
\( \Rightarrow g\left( x \right) = \ln \left( {x + 1} \right) - \dfrac{{x + 2}}{{x + 1}} = 0\) (2) có tối đa 1 nghiệm trên \(\left( {1; + \infty } \right)\).
Mà \(g\left( 2 \right) = \ln 3 - \dfrac{4}{3} < 0,\,\,g\left( 4 \right) = \ln 5 - \dfrac{6}{5} > 0 \Rightarrow \) PT (2) có nghiệm duy nhất \({x_0} \in \left( {2;4} \right)\).
Ta có BBT của \(f\left( x \right)\) trên 2 khoảng \(\left( {0;2} \right)\) và \(\left( {4; + \infty } \right)\) như sau:
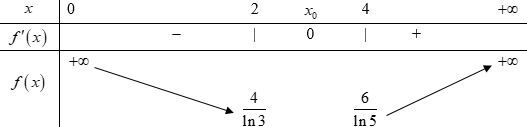
\(\left( {\dfrac{4}{{\ln 3}} \approx 3,64,\,\,\dfrac{6}{{\ln 5}} \approx 3,73} \right)\)
Như vậy, để phương trình đã cho có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(0 < {x_1} < 2 < 4 < {x_2}\) thì \(m > \dfrac{6}{{\ln 5}} \approx 3,73\,\).
Hướng dẫn giải:
- Cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\).
- Khảo sát và lập BBT của hàm số \(f\left( x \right)\), từ đó suy ra điều kiện của \(m\) để thỏa mãn yêu cầu bài toán.
ĐKXĐ: \(x > - 1\).
Ta có: \(m\ln \left( {x + 1} \right) - x - 2 = 0 \Leftrightarrow m\ln \left( {x + 1} \right) = x + 2\) (1)
Dễ dàng kiểm tra \(x = 0\) không phải nghiệm của phương trình trên.
Với \(x \ne 0\), phương trình \(\left( 1 \right) \Leftrightarrow m = \dfrac{{x + 2}}{{\ln \left( {x + 1} \right)}}\)
Xét hàm số \(f\left( x \right) = \dfrac{{x + 2}}{{\ln \left( {x + 1} \right)}}\,\,\left( {x > - 1,\,\,x \ne 0} \right)\) ta có: \(f'\left( x \right) = \dfrac{{\ln \left( {x + 1} \right) - \dfrac{{x + 2}}{{x + 1}}}}{{{{\ln }^2}\left( {x + 1} \right)}}\)
Nhận xét: Trên \(\left( { - 1; + \infty } \right)\backslash \left\{ 0 \right\}\), hàm số \(y = \ln (x + 1)\) đồng biến, hàm số \(y = \dfrac{{x + 2}}{{x + 1}}\) nghịch biến
\( \Rightarrow g\left( x \right) = \ln \left( {x + 1} \right) - \dfrac{{x + 2}}{{x + 1}} = 0\) (2) có tối đa 1 nghiệm trên \(\left( {1; + \infty } \right)\).
Mà \(g\left( 2 \right) = \ln 3 - \dfrac{4}{3} < 0,\,\,g\left( 4 \right) = \ln 5 - \dfrac{6}{5} > 0 \Rightarrow \) PT (2) có nghiệm duy nhất \({x_0} \in \left( {2;4} \right)\).
Ta có BBT của \(f\left( x \right)\) trên 2 khoảng \(\left( {0;2} \right)\) và \(\left( {4; + \infty } \right)\) như sau:
\(\left( {\dfrac{4}{{\ln 3}} \approx 3,64,\,\,\dfrac{6}{{\ln 5}} \approx 3,73} \right)\)
Như vậy, để phương trình đã cho có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(0 < {x_1} < 2 < 4 < {x_2}\) thì \(m > \dfrac{6}{{\ln 5}} \approx 3,73\,\).
Hướng dẫn giải:
- Cô lập \(m\), đưa phương trình về dạng \(m = f\left( x \right)\).
- Khảo sát và lập BBT của hàm số \(f\left( x \right)\), từ đó suy ra điều kiện của \(m\) để thỏa mãn yêu cầu bài toán.
CÂU HỎI CÙNG CHỦ ĐỀ
Tập nghiệm của bất phương trình \({\left( {2 + \sqrt 3 } \right)^{\dfrac{{x - 3}}{{x - 1}}}} < {\left( {2 - \sqrt 3 } \right)^{\dfrac{{x - 1}}{{x - 3}}}}\) là :
Tổng các nghiệm của phương trình \({3^{{x^4} - 3{x^2}}} = 81\)
Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .
Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\) nghiệm đúng với mọi giá trị \(x \in \left[ {1;64} \right]\).
Tập nghiệm của bất phương trình \({\left( {{x^2} + x + 1} \right)^x} < 1\) là:
Cho x>0; \(x \ne 1\) thỏa mãn biểu thức $\dfrac{1}{{{{\log }_2}x}} + \dfrac{1}{{{{\log }_3}x}} + ... + \dfrac{1}{{{{\log }_{2017}}x}} = M$ . Khi đó $x$ bằng:
Tập xác định của hàm số \(f\left( x \right) = \sqrt {{{\log }_{\dfrac{1}{2}}}\dfrac{{3 - 2x - {x^2}}}{{x + 1}}} \) là:
Phương trình \({4^{2x + 5}} = {2^{2 - x}}\) có nghiệm là:
Điều kiện xác định của hệ phương trình \(\left\{ \begin{array}{l}{\log _2}\left( {{x^2} - 1} \right) + {\log _2}\left( {y - 1} \right) = 1\\{3^x} = {3^y}\end{array} \right.\) là:
Tâp nghiệm của bất phương trình \({2^{x + 2}} < {\left( {\dfrac{1}{4}} \right)^x}\) là:
Cho phương trình ${\log _2}\left[ {{{\log }_{\dfrac{1}{8}}}\left( {{x^3}} \right) + {{\log }_2}x + x + 1} \right] = 3.$ Mệnh đề nào sau đây là đúng?
