Cho hình lăng trụ xiên $ABC.A’B’C’$ có đáy $ABC$ là tam giác đều với tâm $O$. Hình chiếu của $C’$ trên $(ABC) $ là $O$. Tính thể tích của lăng trụ biết rằng khoảng cách từ $O$ đến $CC’$ là $a$ và 2 mặt bên $(ACC’A’)$ và $(BCC’B’)$ hợp với nhau góc \({90^0}\).

Đáp án đúng: d

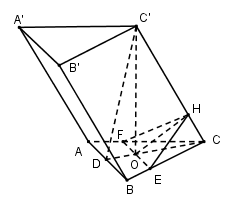
Gọi $D$ là trung điểm của $AB$. Trong $(CC’D)$ kẻ \(OH \bot CC' \Rightarrow OH = a\)

\(\left. \begin{array}{l}CD \bot AB\\C'O \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {CC'D} \right) \Rightarrow AB \bot CC'\)

Trong $(ABC)$, qua $O$ kẻ $EF // AB$ \(\left( {E \in BC;F \in AC} \right)\)

Ta có: \(\left. \begin{array}{l}EF \bot CC'\\OH \bot CC'\end{array} \right\} \Rightarrow CC' \bot \left( {EFH} \right) \Rightarrow CC' \bot HE;CC' \bot HF\)

Ta có: \(\left. \begin{array}{l}\left( {ACC'A'} \right) \cap \left( {BCC'B'} \right) = CC'\\\left( {ACC'A'} \right) \supset HF \bot CC'\\\left( {BCC'B'} \right) \supset HE \bot CC'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ACC'A'} \right);\left( {BCC'B'} \right)} \right)} = \widehat {\left( {HF;HE} \right)} = {90^0} \Rightarrow HE \bot HF\)

\( \Rightarrow \Delta HEF\) vuông tại $H$

\(\Delta HCE = \Delta HCF\left( {c.g.v - c.h} \right) \Rightarrow HE = HF \Rightarrow \Delta HEF\) vuông cân tại H\( \Rightarrow EF = 2HO = 2a\)

Ta có: \(\dfrac{{EF}}{{AB}} = \dfrac{{CO}}{{CD}} = \dfrac{2}{3} \Rightarrow AB = \dfrac{3}{2}EF = \dfrac{3}{2}.2a = 3a\)\( \Rightarrow {S_{\Delta ABC}} = \dfrac{{A{B^2}\sqrt 3 }}{4} = \dfrac{{9{a^2}\sqrt 3 }}{4}\)

\(CD = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{3a\sqrt 3 }}{2} \Rightarrow CO = \dfrac{2}{3}AB = \dfrac{2}{3}.\dfrac{{3a\sqrt 3 }}{2} = a\sqrt 3 \)

\(C'O \bot \left( {ABC} \right) \Rightarrow C'O \bot CO \Rightarrow \Delta CC'O\) vuông tại O

\( \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{C'{O^2}}} + \dfrac{1}{{C{O^2}}} \Rightarrow \dfrac{1}{{C'{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{C{O^2}}} = \dfrac{1}{{{a^2}}} - \dfrac{1}{{3{a^2}}} = \dfrac{2}{{3{a^2}}} \Rightarrow C'O = \dfrac{{\sqrt 6 }}{2}a\)

Vậy ${V_{ABC.A'B'C'}} = C'O.{S_{\Delta ABC}} = \dfrac{{a\sqrt 6 }}{2}.\dfrac{{9{a^2}\sqrt 3 }}{4} = \dfrac{{27{a^3}\sqrt 2 }}{8}$

Hướng dẫn giải:

- Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng nằm trong các mặt phẳng mà cùng vuông góc với giao tuyến.

- Tính độ dài đường cao và diện tích đáy lăng trụ.

- Tính thể tích lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao.