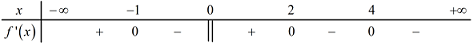Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\).
\(y' = 3a{x^2} + 2bx + c\).
Dựa vào BBT ta thấy hàm số có hai điểm cực trị \({x_1} = - 1,\,\,{x_2} = 2\) nên phương trình \(y' = 0\) có hai nghiệm phân biệt thỏa mãn \(S = {x_1} + {x_2} = 1 > 0\), \(P = {x_1}{x_2} = - 2 < 0\) \( \Rightarrow \left\{ \begin{array}{l}\Delta ' = {b^2} - 3ac > 0\\S = \dfrac{{ - 2b}}{{3a}} > 0\\P = \dfrac{c}{{3a}} < 0\end{array} \right.\).
Mà \(a < 0\) nên \(b > 0\) và \(c > 0\).
Dựa vào BBT ta thấy tại điểm \(x = 0\) thì \(y > 0\), do đó \(d > 0\).
Vậy trong 4 hệ số a, b, c, d chỉ có 1 số âm.
Hướng dẫn giải:
- Dựa vào \(\mathop {\lim }\limits_{x \to + \infty } y\) xác định dấu của hệ số a.
- Dựa vào số điểm cực trị suy ra dấu của hệ số b.
- Dựa vào dấu của tích hai điểm cực trị suy ra dấu của hệ số c.
- Thay \(x = 0\) vào hàm số và xác định dấu của d.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\).
\(y' = 3a{x^2} + 2bx + c\).
Dựa vào BBT ta thấy hàm số có hai điểm cực trị \({x_1} = - 1,\,\,{x_2} = 2\) nên phương trình \(y' = 0\) có hai nghiệm phân biệt thỏa mãn \(S = {x_1} + {x_2} = 1 > 0\), \(P = {x_1}{x_2} = - 2 < 0\) \( \Rightarrow \left\{ \begin{array}{l}\Delta ' = {b^2} - 3ac > 0\\S = \dfrac{{ - 2b}}{{3a}} > 0\\P = \dfrac{c}{{3a}} < 0\end{array} \right.\).
Mà \(a < 0\) nên \(b > 0\) và \(c > 0\).
Dựa vào BBT ta thấy tại điểm \(x = 0\) thì \(y > 0\), do đó \(d > 0\).
Vậy trong 4 hệ số a, b, c, d chỉ có 1 số âm.
Hướng dẫn giải:
- Dựa vào \(\mathop {\lim }\limits_{x \to + \infty } y\) xác định dấu của hệ số a.
- Dựa vào số điểm cực trị suy ra dấu của hệ số b.
- Dựa vào dấu của tích hai điểm cực trị suy ra dấu của hệ số c.
- Thay \(x = 0\) vào hàm số và xác định dấu của d.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy $ABCD$ là hình vuông cạnh bằng $a$. Hình chiếu vuông góc của điểm $A'$ trên mặt phẳng $\left( {ABCD} \right)$ là trung điểm $I$ của cạnh $AB$. Biết \(A'C\) tạo với mặt phẳng đáy một góc \(\alpha \) với \(\tan \alpha = \dfrac{2}{{\sqrt 5 }}\). Thể tích khối chóp $A'.ICD$ là:
Hàm số $y = {x^3} + 2a{x^2} + 4bx - 2018,{\mkern 1mu} {\mkern 1mu} (a,{\mkern 1mu} b \in R)$ đạt cực trị tại $x = - 1$ . Khi đó hiệu $a - b$ là:
Cho hình chóp đều $S.ABCD$ có diện tích đáy là \(16c{m^2}\), diện tích một mặt bên là \(8\sqrt 3 c{m^2}\). Thể tích khối chóp $S.ABCD$ là:
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(C,\)\(AB = a\sqrt 5 ,\)\(AC = a.\) Cạnh bên \(SA = 3a\) và vuông góc với mặt phẳng đáy. Thể tích của khối chóp \(S.ABC\) bằng
Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Tính thể tích khối chóp \(S.ABC\).
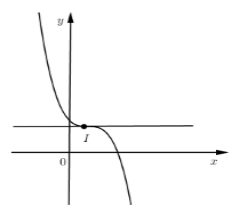
Hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ, chọn kết luận đúng:
Cho hình chóp tứ giác $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, \(SA \bot (ABCD)\) và \(SA = a\sqrt 6 \). Thể tích của khối chóp $S.ABCD$ bằng
Khối đa diện đều nào sau đây có các mặt không phải là tam giác đều

Cho biết GTLN của hàm số $f\left( x \right)$ trên $\left[ {1;3} \right]$ là $M = - 2$. Chọn khẳng định đúng:
Vật thể nào trong các vật thể sau không phải là khối đa diện?

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sin x$ trên đoạn $\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]$ lần lượt là
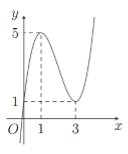
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( x \right) = 3\) là:
Một nhà máy cần thiết kế một chiếc bể đựng nước hình trụ bằng tôn có nắp, có thể tích là \(64\pi \left( {{m^3}} \right)\). Tìm bán kính đáy \(r\) của hình trụ sao cho hình trụ được làm ra tốn ít nhiên liệu nhất.
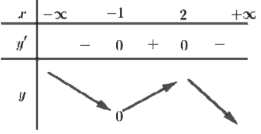
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm như hình bên. Số điểm cực trị của hàm số đã cho là: