Bà Hoa gửi $100$ triệu vào tài khoản định kì tính lãi suất là $8\% $ một năm. Sau 5 năm, bà rút toàn bộ số tiền và dùng một nửa để sửa nhà, còn một nửa tiền bà lại đem gửi ngân hàng trong 5 năm với cùng lãi suất. Tính số tiền lãi thu được sau 10 năm.
A.
$81,412$ triệu
B.
$115,892$ triệu
C.
$119$ triệu
D.
$78$ triệu
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: a
Số tiền bà Hoa rút sau 5 năm đầu là: $100{\left( {1 + 8\% } \right)^5} = 146,932$ triệu.
Số tiền lãi lần 1 là: $146,932 - 100 = 46,932$ triệu.
Số tiền bà gửi tiếp vào ngân hàng là: $146,932:2 = 73,466$ triệu
Số tiền và có sau 5 năm là: $73,466{\left( {1 + 8\% } \right)^5} = 107,946$ triệu.
Số tiền lãi lần 2 là: $107,946 - 73,466 = 34,480$ triệu.
Tổng số tiền lãi sau 2 lần là: $46,932 + 34,480 = 81,412$ triệu.
Hướng dẫn giải:
- Tính số tiền bà Hoa rút ra sau 5 năm theo công thức $T = A{\left( {1 + r} \right)^N}$.
- Tính số tiền lãi lần đầu.
- Tính số tiền bà đem gửi lần 2.
- Tính số tiền sau 5 năm lần 2 theo công thức: $T = A{\left( {1 + r} \right)^N}$
- Tính số tiền lãi lần 2 và suy ra đáp số.
Số tiền bà Hoa rút sau 5 năm đầu là: $100{\left( {1 + 8\% } \right)^5} = 146,932$ triệu.
Số tiền lãi lần 1 là: $146,932 - 100 = 46,932$ triệu.
Số tiền bà gửi tiếp vào ngân hàng là: $146,932:2 = 73,466$ triệu
Số tiền và có sau 5 năm là: $73,466{\left( {1 + 8\% } \right)^5} = 107,946$ triệu.
Số tiền lãi lần 2 là: $107,946 - 73,466 = 34,480$ triệu.
Tổng số tiền lãi sau 2 lần là: $46,932 + 34,480 = 81,412$ triệu.
Hướng dẫn giải:
- Tính số tiền bà Hoa rút ra sau 5 năm theo công thức $T = A{\left( {1 + r} \right)^N}$.
- Tính số tiền lãi lần đầu.
- Tính số tiền bà đem gửi lần 2.
- Tính số tiền sau 5 năm lần 2 theo công thức: $T = A{\left( {1 + r} \right)^N}$
- Tính số tiền lãi lần 2 và suy ra đáp số.
CÂU HỎI CÙNG CHỦ ĐỀ
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
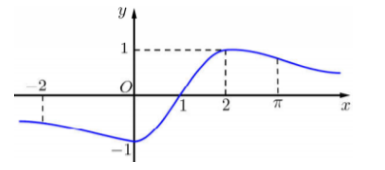
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
Cho hàm số $y = {x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2}$$\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số $\left( 1 \right)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ ${x_1},{x_2},{x_3},{x_4}$ thoả mãn ${x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 = 6$
Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới đây
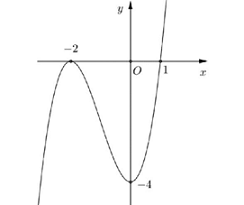
Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 5;5} \right)\) để phương trình \({f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0\) có \(6\) nghiệm phân biệt
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{2x + c}}\) có tiệm cận ngang \(y = 2\) và tiệm cận đứng \(x = 1\) thì \(a + c\) bằng
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
Công thức nào sau đây là công thức tăng trưởng mũ?
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
Hàm số nào dưới đây có tập xác định bằng \(\mathbb{R}\)?

