Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
Ta có \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } {\mkern 1mu} \dfrac{{ax + b}}{{2x + c}} = \dfrac{a}{2} \Rightarrow y = \dfrac{a}{2}\) là tiệm cận ngang của ĐTHS
\( \Rightarrow \dfrac{a}{2} = 2 \Rightarrow a = 4.\)
Và \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} - {\kern 1pt} \dfrac{c}{2}} {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} - {\kern 1pt} \dfrac{c}{2}} {\mkern 1mu} \dfrac{{ax + b}}{{2x + c}} = \infty \Rightarrow x = - \dfrac{c}{2}\) là tiệm cận đứng của ĐTHS
\( \Rightarrow - \dfrac{c}{2} = 1 \Rightarrow c = - {\mkern 1mu} 2.\)
Vậy tổng \(a + c = 4 - 2 = 2.\)
Hướng dẫn giải:
Xác định được hai đường tiệm cận của đồ thị hàm số bậc nhất trên bậc nhất
Ta có \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } {\mkern 1mu} \dfrac{{ax + b}}{{2x + c}} = \dfrac{a}{2} \Rightarrow y = \dfrac{a}{2}\) là tiệm cận ngang của ĐTHS
\( \Rightarrow \dfrac{a}{2} = 2 \Rightarrow a = 4.\)
Và \(\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} - {\kern 1pt} \dfrac{c}{2}} {\mkern 1mu} y = \mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} - {\kern 1pt} \dfrac{c}{2}} {\mkern 1mu} \dfrac{{ax + b}}{{2x + c}} = \infty \Rightarrow x = - \dfrac{c}{2}\) là tiệm cận đứng của ĐTHS
\( \Rightarrow - \dfrac{c}{2} = 1 \Rightarrow c = - {\mkern 1mu} 2.\)
Vậy tổng \(a + c = 4 - 2 = 2.\)
Hướng dẫn giải:
Xác định được hai đường tiệm cận của đồ thị hàm số bậc nhất trên bậc nhất
CÂU HỎI CÙNG CHỦ ĐỀ
Với \(a\) và \(b\) là hai số thực dương tùy ý, \(\log \left( {a{b^2}} \right)\) bằng
Cho \(f\left( x \right)\) mà đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên
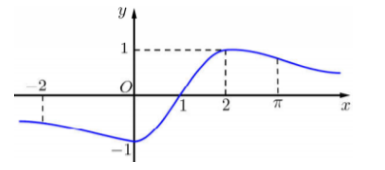
Bất phương trình \(f\left( x \right) > \sin \dfrac{{\pi x}}{2} + m\) nghiệm đúng với mọi \(x \in \left[ { - 1;3} \right]\) khi và chỉ khi:
Tìm $m$ để hàm số $y = \dfrac{{{x^3}}}{3} - 2m{x^2} + 4mx + 2$ nghịch biến trên khoảng $\left( { - 2;0} \right)$.
Cho hàm số $y = {x^4} - 2\left( {2m + 1} \right){x^2} + 4{m^2}$$\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số $\left( 1 \right)$ cắt trục hoành tại $4$ điểm phân biệt có hoành độ ${x_1},{x_2},{x_3},{x_4}$ thoả mãn ${x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 = 6$
Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình dưới đây
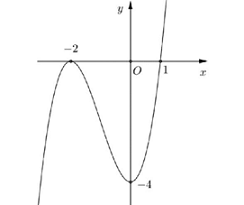
Có tất cả bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 5;5} \right)\) để phương trình \({f^2}(x) - (m + 4)\left| {f(x)} \right| + 2m + 4 = 0\) có \(6\) nghiệm phân biệt
Tìm tất cả các giá trị của $m$ để hàm số $y = - \dfrac{1}{3}{x^3} + \dfrac{{m{x^2}}}{3} + 4$ đạt cực đại tại $x = 2?$
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
Cho hình chóp đều $S.ABCD$ có cạnh đáy bằng $2a$. Khoảng cách giữa hai đường thẳng $SA$ và $CD$ bằng \(a\sqrt 3 \). Thể tích khối chóp $S.ABCD$ là:
Công thức nào sau đây là công thức tăng trưởng mũ?
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
Hàm số nào dưới đây có tập xác định bằng \(\mathbb{R}\)?
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều ?
Kết luận nào đúng về số thực \(a\) nếu \({\left( {\dfrac{1}{a}} \right)^{ - 0,2}} < {a^2}\)

