Trường hợp bằng nhau thứ ba của tam giác

Trường hợp bằng nhau thứ ba góc cạnh góc và trường hợp bằng nhau cạnh huyền-góc vuông môn toán lớp 7 với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(390) 1300 02/08/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    1. Các kiến thức cần nhớ

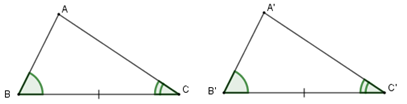
    Trường hợp bằng nhau thứ ba của tam giác

    Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác vuông kia thì hai tam giác đó bằng nhau.

    Ví dụ:

     \(\left. \begin{array}{l}\widehat B = \widehat B'\\BC = B'C'\\\widehat C = \widehat C'\end{array} \right\}\)\( \Rightarrow \Delta ABC = \Delta A'B'C'\,\,(g.c.g)\)

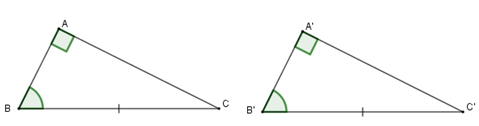
    Trường hợp bằng nhau cạnh huyền – góc nhọn của tam giác vuông

    Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

    Ví dụ:

     \(\left. \begin{array}{l}\widehat A = \widehat A' = {90^0}\\BC = B'C'\\\widehat B = \widehat B'\end{array} \right\}\)\( \Rightarrow \Delta ABC = \Delta A'B'C'\left( {ch.gn} \right)\)

    2. Các dạng toán thường gặp

    Dạng 1: Chứng minh hai tam giác bằng nhau theo trường hợp góc-cạnh-góc

    Phương pháp:

    Sử dụng trường hợp bằng nhau góc- cạnh-góc của tam giác và trường hợp bằng nhau cạnh huyền-góc nhọn của tam giác vuông.

    Dạng 2: Chứng minh hai đoạn thẳng bằng nhau. Tính độ dài đoạn thẳng.

    Phương pháp:

    + Chọn hai tam giác chứa các đoạn thẳng cần tính.

    + Chứng minh hai tam giác bằng nhau theo trường hợp góc cạnh góc

    + Suy ra các yếu tố cần thiết để giải bài toán.

    Dạng 3: Bài toán sử dụng nhiều trường hợp bằng nhau của tam giác

    Phương pháp:

    Sử dụng các trường hợp bằng nhau đã học của tam giác: cạnh-cạnh-cạnh, cạnh-góc-cạnh, góc-cạnh-góc…và các trường hợp bằng nhau của tam giác vuông.

    Xem toàn bộ nội dung Toán 7:

    (390) 1300 02/08/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 7 Toán 7