Tam giác cân

Lý thuyết về tam giác cân, tam giác vuông cân, tam giác đều môn toán lớp 7 phần hình học với nhiều dạng bài cùng phương pháp giải nhanh kèm bài tập vận dụng
(390) 1301 02/08/2022
Bài viết đã được lưu
Chia sẻ

Nội dung bài viết

    Xem thêm

    I. Các kiến thức cần nhớ

    1. Tam giác cân

    Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.

    Ví dụ: \(\Delta ABC\) cân tại A \( \Leftrightarrow AB = AC\)

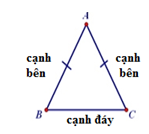
    Tính chất:

    Trong tam giác cân, hai góc ở đáy bằng nhau.

    Ví dụ: \(\Delta ABC\) cân tại A \( \Rightarrow \widehat B = \widehat C\)

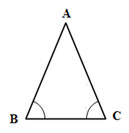
    Dấu hiệu nhận biết

    + Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

    + Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

    2. Tam giác vuông cân

    Định nghĩa: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.

    Ví dụ: \(\Delta ABC\) vuông cân tại A \( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = {90^0}\\AB = AC\end{array} \right.\)

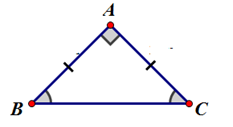
    Tính chất

    Mỗi góc nhọn của tam giác vuông cân bằng \({45^0}.\)

    Ví dụ: \(\Delta ABC\) vuông cân tại A \( \Rightarrow \widehat B = \widehat C = {45^0}.\)

    3. Tam giác đều

    Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.

    Ví dụ: \(\Delta ABC\) đều \( \Leftrightarrow AB = BC = CA\)

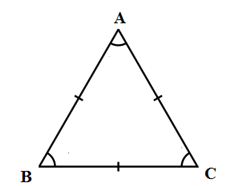
    Tính chất

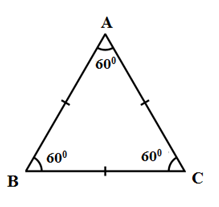
    Trong tam giác đều, mỗi góc bằng \({60^0}.\)

    Ví dụ: \(\Delta ABC\) đều \( \Rightarrow \widehat A = \widehat B = \widehat C = {60^0}.\)

    Dấu hiệu nhận biết

    + Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều

    + Nếu tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.

    + Nếu một tam giác cân có một góc bằng \({60^0}\) thì tam giác đó là tam giác đều.

    II. Các dạng toán thường gặp

    Dạng 1: Nhận biết một tam giác là tam giác cân, tam giác vuông cân, tam giác đều

    Phương pháp:

    Dựa vào dấu hiệu nhận biết tam giác cân, tam giác vuông cân, tam giác đều.

    Dạng 2: Chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc

    Phương pháp:

    Sử dụng định nghĩa và tính chất của tam giác cân, tam giác vuông cân và tam giác đều.

    Xem toàn bộ nội dung Toán 7:

    (390) 1301 02/08/2022
    Bài viết đã được lưu
    Bài trước
    Chia sẻ
    Bài sau  
    Tìm thêm: Lý thuyết Lý thuyết lớp 7 Toán 7