Ôn tập chương 2: Hàm số và đồ thị

1. Đại lượng tỉ lệ thuận

a) Định nghĩa đại lượng tỉ lệ thuận

b) Tính chất:

* Nếu hai đại lượng tỉ lệ thuận với nhau thì:

+ Tỉ số hai giá trị tương ứng của chúng luôn luôn không đổi.

+ Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia.

* Nếu hai đại lượng $y$ và $x$  tỉ lệ thuận với nhau theo tỉ số $k$ thì: $y = kx;$

$\dfrac{{{y_1}}}{{{x_1}}} = \dfrac{{{y_2}}}{{{x_2}}} = \dfrac{{{y_3}}}{{{x_3}}} = ... = k$ ; $\dfrac{{{x_1}}}{{{x_2}}} = \dfrac{{{y_1}}}{{{y_2}}};\dfrac{{{x_1}}}{{{x_3}}} = \dfrac{{{y_1}}}{{{y_3}}};...$

2. Đại lượng tỉ lệ nghịch

a) Định nghĩa

b) Tính chất

* Nếu hai đại lượng tỉ lệ nghịch với nhau thì:

+ Tích hai giá trị tương ứng của chúng luôn luôn không đổi.

+ Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia.

* Nếu hai đại lượng y và x tỉ lệ nghịch với nhau theo hệ số tỉ lệ $a$  thì:

${x_1}{y_1} = {x_2}{y_2} = {x_3}{y_3} = ... = a$

$\dfrac{{{x_1}}}{{{x_2}}} = \dfrac{{{y_2}}}{{{y_1}}};\dfrac{{{x_1}}}{{{x_3}}} = \dfrac{{{y_3}}}{{{y_1}}};...$

3. Hàm số

a) Định nghĩa hàm số

Nếu đại lượng $y$  phụ thuộc vào đại lượng thay đổi $x$  sao cho với mỗi giá trị của $x$  ta luôn xác định được chỉ một giá trị tương ứng của $y$ thì $y$được gọi là hàm số của $x$ và $x$ gọi là biến số.

Nhận xét: Nếu đại lượng $y$ là hàm số của đại lượng $x$  thì mỗi giá trị của đại lượng $x$ đều có một giá trị tương ứng duy nhất của đại lượng $y$ ( hay mỗi giá trị của $x$ không thể có hơn một giá trị tương ứng của đại lượng $y$).

Chú ý:

+ Khi $x$  thay đổi mà $y$  luôn nhận một giá trị thì $y$ được gọi là hàm hằng.

+ Hàm số có thể được cho bằng bảng, bằng công thức,…

+ Khi $y$ là hàm số của $x$  ta có thể viết: $y = f\left( x \right);y = g\left( x \right);...$

b) Mặt phẳng tọa độ

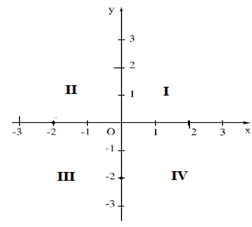
+ Mặt phẳng tọa độ $Oxy$ ( mặt phẳng có hệ trục tọa độ $Oxy$ ) được xác định bởi hai trục số vuông góc với nhau: trục hoảnh $Ox$  và trục tung $Oy$ ; điểm $O$  là gốc tọa độ.

+ Hai trục tọa độ chia mặt phẳng tọa độ thành bốn góc phần tư thứ I, II, III, IV theo thứ tự ngược chiều kim đồng hồ.

* Tọa độ một điểm:

Trên mặt phẳng tọa độ:

+ Mỗi điểm $M$  xác định một cặp số $\left( {{x_0};{y_0}} \right).$ Ngược lại mỗi cặp số $\left( {{x_0};{y_0}} \right)$ xác định một điểm $M$ .

+ Cặp số $\left( {{x_0};{y_0}} \right)$ gọi là tọa độ của điểm $M$ , ${x_0}$ là hoành độ, ${y_0}$ là tung độ của điểm $M.$

+ Điểm $M$ có tọa độ $\left( {{x_0};{y_0}} \right)$ kí hiệu là $M\left( {{x_0};{y_0}} \right).$

c) Đồ thị của hàm số $y = f\left( x \right)$

+ Đồ thị của hàm số $y = f\left( x \right)$ là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x;y) trên mặt phẳng tọa độ.

+ Một điểm $H$  thuộc đồ thị $\left( H \right)$ của hàm số $y = f\left( x \right)$ thì có tọa độ thỏa mãn đẳng thức $y = f\left( x \right)$ và ngược lại.

$M\left( {{x_0};{y_0}} \right) \in \left( H \right) \Rightarrow {y_0} = f\left( {{x_0}} \right)$

4. Đồ thị của hàm số $y = ax\,\left( {a \ne 0} \right)$

+ Đồ thị của hàm số $y = ax\left( {a \ne 0} \right)$là một đường thẳng đi qua gốc tọa độ.

+ Cách vẽ: Vẽ đường thẳng đi qua điểm $O(0; 0)$ và $A(1; a)$