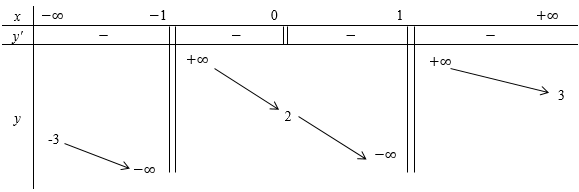
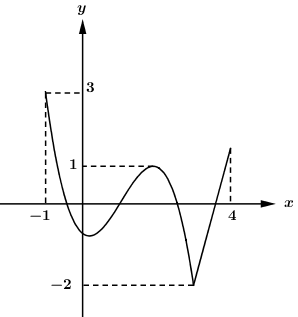
Đồ thị hàm số $y = \dfrac{{x - 3}}{{{x^2} + x - 2}}$ có bao nhiêu đường tiệm cận đứng?
lượt xem
Cho hàm số $y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx.$ Tìm $m$ để đồ thị hàm số có hai điểm cực trị là $A, B$ sao cho đường thẳng $AB$ vuông góc với $d:\,x - y - 9 = 0$
lượt xem
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
lượt xem
Cho hàm số: $f(x) = - 2{x^3} + 3{x^2} + 12x - 5.$ Trong các mệnh đề sau, tìm mệnh đề sai?
lượt xem
Với điều kiện các logarit đều có nghĩa, chọn mệnh đề đúng:
lượt xem
Hàm số nào sau đây có đồ thị như hình vẽ?
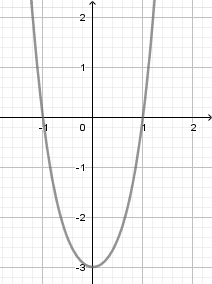
lượt xem
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là sai?
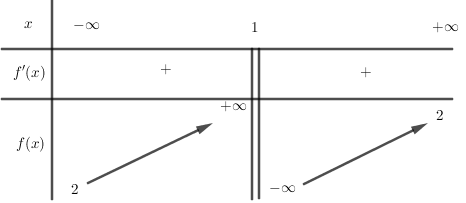
lượt xem
Trong các hình dưới đây, hình nào là khối đa diện?
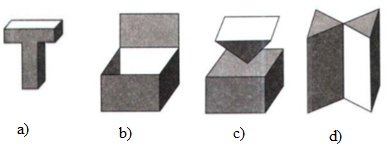
lượt xem
Công thức nào sau đây là công thức tăng trưởng mũ?
lượt xem
Cho hai đồ thị hàm số $y = {x^3} + 2{x^2} - x + 1$ và đồ thị hàm số $y = {x^2} - x + 3$ có tất cả bao nhiêu điểm chung?
lượt xem
Hai hình tứ diện có các cạnh tương ứng bằng nhau thì chúng:
lượt xem
Đáy của hình chóp $S.ABCD$ là một hình vuông cạnh \(a\). Cạnh bên \(SA\) vuông góc với mặt đáy và có độ dài là \(a\). Thể tích khối tứ diện \(S.BCD\) bằng:
lượt xem
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là tứ giác đều cạnh $a$, biết rằng \(BD' = a\sqrt 6 \) . Tính thể tích của khối lăng trụ?
lượt xem
Cho $n \in Z, n>0$, với điều kiện nào của $a$ thì đẳng thức sau xảy ra: ${a^{ - n}} = \dfrac{1}{{{a^n}}}$?
lượt xem
Cho khối chóp S.ABCD có thể tích bằng \(4{a^3}\), đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SD. Biết diện tích tam giác SAB bằng \({a^2}\). Tính khoảng cách từ M tới mặt phẳng \(\left( {SAB} \right)\).
lượt xem
Tính giá trị của biểu thức \({3^2}{.5^{2 + 2\sqrt 2 }}:{25^{\left( {1 + \sqrt 2 } \right)}}\) có kết quả là:
lượt xem
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
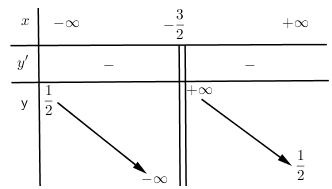
Bảng biến thiên trên là bảng biến thiên của đồ thị hàm số nào?
lượt xem
Số mặt phẳng đối xứng của mặt cầu là:
lượt xem
lượt xem
Chọn kết luận đúng:
lượt xem
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
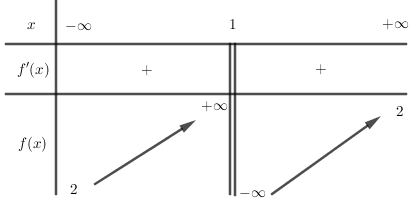
lượt xem
Cho các đồ thị hàm số \(y = {a^x},y = {b^x},y = {c^x}\left( {0 < a,b,c \ne 1} \right)\), chọn khẳng định đúng:
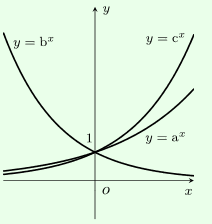
lượt xem
Biết đồ thị các hàm số $y = {x^3} + \dfrac{5}{4}x - 2$ và $y = {x^2} + x - 2$ tiếp xúc nhau tại điểm $M({x_0}\,;\,{y_0})$. Tìm ${x_0}.$
lượt xem
Tính giá trị \({\left( {\dfrac{1}{{16}}} \right)^{ - 0,75}} + {\left( {\dfrac{1}{8}} \right)^{ - \frac{4}{3}}},\)ta được kết quả là:
lượt xem
Khối mười hai mặt đều là khối đa diện đều loại:
lượt xem
Tính giá trị của biểu thức \(P = {\left( {2\sqrt 6 - 5} \right)^{2020}}{\left( {2\sqrt 6 + 5} \right)^{2021}}\).
lượt xem
Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng:
“Số cạnh của một hình đa diện luôn……………….số mặt của hình đa diện ấy”
lượt xem
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là:
lượt xem
Chọn mệnh đề đúng:
lượt xem
Xét hàm số \(y = {x^\alpha }\) trên tập \(\left( {0; + \infty } \right)\) có đồ thị dưới đây, chọn kết luận đúng:

lượt xem
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên:

Hàm số \(y = - 2f\left( x \right)\) đồng biến trên khoảng:
lượt xem
Hàm số \(y = {\log _{\frac{e}{3}}}\left( {x - 1} \right)\) nghịch biến trên khoảng nào dưới đây?
lượt xem
Cho hàm số $f\left( x \right)$ xác định và liên tục trên $R$, có $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty ;\mathop {\lim }\limits_{x \to - \infty } f(x) = - \infty $ , khi đó:
lượt xem
Chọn kết luận đúng: Đồ thị hàm số bậc bốn trùng phương
lượt xem
Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) biết \(a > 0\), \(c > 2017\) và \(a + b + c < 2017\). Số điểm cực trị của hàm số \(y = \left| {f\left( x \right) - 2017} \right|\) là:
lượt xem
Cho các số thực $x, y$ thỏa mãn ${\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} + 2xy \leqslant 32.$ Giá trị nhỏ nhất $m$ của biểu thức $A = {x^3} + {y^3} + 3\left( {xy - 1} \right)\left( {x + y - 2} \right)$ là:
lượt xem
lượt xem
Cho hình hộp đứng $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình thoi cạnh $a$ và $\widehat {BAD} = {60^0}$, $AB’$ hợp với đáy $(ABCD)$ một góc ${30^0}$. Thể tích của khối hộp là
lượt xem
Cho tứ diện \(ABCD\) có \(AD = 14,BC = 6\). Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AC,BD\) và \(MN = 8\). Gọi \(\alpha \) là góc giữa hai đường thẳng \(BC\) và \(MN\). Tính \(\sin \alpha \).
lượt xem
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy ABC là tam giác vuông tại B với \(AB = a,AA' = 2a,\)\(A'C = 3a\) . Gọi M là trung điểm của \(A'C'\), I là giao điểm của đường thẳng AM và A’C. Tính theo a thể tích khối IABC .
lượt xem
Cho khối lăng trụ tam giác đều \(ABC.{A_1}{B_1}{C_1}\) có tất cả các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(A{A_1}\). Thể tích khối chóp \(M.BC{A_1}\) là:
lượt xem
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\). Biết \(f\left( {x + 1} \right) = {x^3} + 3{x^2} + 3x + 2\). Hãy xác định biểu thức \(f\left( x \right)\).
lượt xem
Cho hàm số \(y=\frac{x-1}{2x-3}\). Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ I đến tiếp tuyến của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng
lượt xem
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên
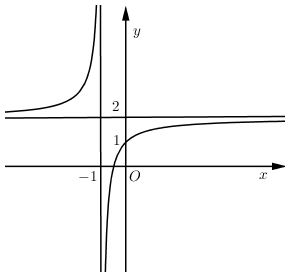
Chọn khẳng định đúng:
lượt xem
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
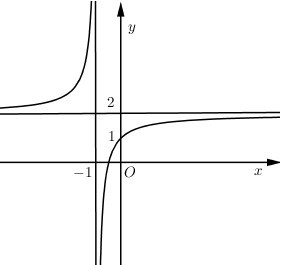
Chọn kết luận đúng:
lượt xem
Đồ thị trong hình dưới là đồ thị của một trong bốn hàm số cho trong các phương án sau đây, đó là hàm số nào?
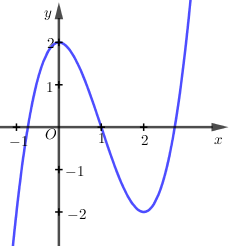
lượt xem
Phương trình đường tiệm cận đứng của đồ thị hàm số $y = \dfrac{{{x^2} - 3x - 4}}{{{x^2} - 16}}$ là:
lượt xem
Cho điểm $I\left( {0;4} \right)$ và đường cong $\left( C \right):y = - {x^2} + 3x$. Phương trình $\left( C \right)$ đối với hệ tọa độ $\left( {IXY} \right)$ là:
lượt xem
lượt xem
Cho hàm số \(y = {x^3} - 3{x^2} - 9x + m\). Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số.
lượt xem