chữ số thập phân thứ hai là số 1, sau nó là số 5 nên ta công thêm 1 và 1, vậy số làm tròn là 0,92

36 có hai căn bậc hai là \(\sqrt{36}=6\) và \(-\sqrt{36}=-6\)

\(\sqrt{169} =13\in N\) nên A đúng

Q là tập hợp các số vô tỉ nên là con của tập hợp các số thực R

\(\sqrt 3\) là số thập phân vô hạn không tuần hoàn nên là số vô tỉ, \(\sqrt 3\in I\). Vậy C sai

\({\left( { - \frac{3}{7}} \right)^8}:{\left( {\frac{3}{7}} \right)^6} = {\left( {\frac{3}{7}} \right)^8}:{\left( {\frac{3}{7}} \right)^6} = {\left( {\frac{3}{7}} \right)^2}\)

Mà 2 là số chẵn nên \(\left(\frac{3}{7}\right)^{2}=\left(-\frac{3}{7}\right)^{2}\)

Vậy cả B và C đều đúng

Đẳng thức có thể suy ra đựuc bằng cách đổi chỗ vị trí của a và d, khi dó ta được \(\frac{d}{b}=\frac{c}{a}\)

Ta thấy \(\sqrt {16}=4\) vậy x=16

Ta có 

\(\begin{array}{l} {2^{2x}} = {8^4}\\ {2^{2x}} = {\left( {{2^3}} \right)^4}\\ {2^{2x}} = {2^{12}}\\ 2x = 12\\ x = 6 \end{array}\)

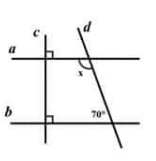
Ta có \(\left\{ \begin{array}{l} a \bot c\\ b \bot c \end{array} \right. \Rightarrow a//b\)

\(\begin{array}{l} \left\{ \begin{array}{l} a//b\\ \text{ góc có số đo x và góc có số đo 70 nằm ở vị trí trong cùng phía} \end{array} \right.\\ \Rightarrow x + {70^o} = {180^o}\\ \,\,\,\,\,\,\,x = {180^0} - {70^0} = {110^0} \end{array}\)

Hai đường thẳng vuông góc là hai đường thẳng cắt nhau và tạo thành góc 90^0.

^{Chọn A}

Theo lý thuyết, hai đường thẳng song song là hai đường thẳng không có điểm chung

Đường thẳng vuông góc với đoạn thẳng đó tại trung điểm

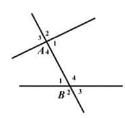
A sai vì \(\hat A_{1} \text{ và }\hat A_{4}\) là hai góc kề bù

B, D sai vì \(\hat A_{2} \text{ và }\hat B_{2}\) là hai góc so le ngoài

C đúng

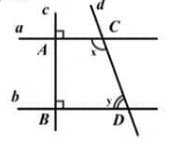
Ta có

\(\left\{\begin{array}{l} a \perp c \\ b \perp c \end{array} \Rightarrow a / / b\right.\)

Do \(\begin{aligned} &\left\{\begin{array}{l} a / / b \\ \text { góc có số đo x và góc có số đo } y \text { nằm ở vị trí trong cùng phía } \end{array}\right.\\ &\Rightarrow x+y=180^{\circ} \end{aligned}\)

Lại có \(\frac{x}{y}=\frac{2}{3}\Leftrightarrow \frac{x}{2}=\frac{y}{3}\)

Theo tính chất dãy tỉ số bằng nhau ta có

\(\begin{array}{l} \frac{x}{2} = \frac{y}{3} = \frac{{x + y}}{{2 + 3}} = \frac{{{{180}^o}}}{5} = {36^0}\\ \frac{x}{2} = {36^0} \Rightarrow x = {72^0}\\ \frac{y}{3} = {36^0} \Rightarrow x = {108^0} \end{array}\)

 A sai vì hai góc bằng nhau có thể không chung đỉnh.

Hai góc gối đỉnh là hai góc có chung 1 đỉnh, mỗi cạnh của góc này là tia đối của một cạnh góc kia

Ta có

\(\begin{array}{l} 1\frac{1}{3} - \frac{3}{4}.\frac{{ - 8}}{5} + \frac{{ - 1}}{5}\\ = \frac{4}{3} + \frac{{24}}{{20}} - \frac{1}{5}\\ = \frac{4}{3} + \frac{6}{5} - \frac{1}{5}\\ = \frac{4}{3} + \left( {\frac{6}{5} - \frac{1}{5}} \right)\\ = \frac{4}{3} + 1 = \frac{7}{3} \end{array}\)

Ta có

\(\begin{array}{l} {\left( {\frac{{ - 1}}{3}} \right)^2} - \left| {\frac{{ - 3}}{2}} \right| + \sqrt {\frac{{25}}{{16}}} \\ = \frac{1}{9} - \frac{3}{2} + \frac{5}{4} = \frac{{4 - 54 + 45}}{{36}} = \frac{{ - 5}}{{36}} \end{array}\)

Ta có

\(\begin{array}{l} \frac{5}{9}:2\frac{2}{5} - 4\frac{5}{9}:2\frac{2}{5}\\ = \frac{5}{9}:\frac{{12}}{5} - \frac{{41}}{9}:\frac{{12}}{5}\\ = \frac{5}{9}.\frac{5}{{12}} - \frac{{41}}{9}.\frac{5}{{12}}\\ = \frac{5}{{12}}\left( {\frac{5}{9} - \frac{{41}}{9}} \right)\\ = \frac{5}{{12}}.\left( { - 4} \right) = \frac{{ - 5}}{3} \end{array}\)

\(\begin{array}{l} \frac{2}{3}:x + \frac{1}{3} = - 7\\ \frac{2}{3}:x\,\,\,\,\,\,\,\,\, = - 7 - \frac{1}{3}\\ \frac{2}{3}:x\,\,\,\,\,\,\,\,\, = \frac{{ - 22}}{2}\\ x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{2}{3}:\frac{{ - 22}}{3}\\ x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \frac{1}{{11}} \end{array}\)

Ta có

\(\begin{array}{l} \frac{3}{4} - \left| {x - \frac{3}{2}} \right| = \frac{1}{6}\\ \,\,\,\,\, - \left| {x - \frac{3}{2}} \right| = \frac{1}{6} - \frac{3}{4}\\ \,\,\,\,\, - \left| {x - \frac{3}{2}} \right| = \frac{{ - 7}}{{12}}\\ \,\,\,\,\,\,\,\,\,\left| {x - \frac{3}{2}} \right| = \frac{7}{{12}}\\ x - \frac{3}{2} = \frac{7}{{12}} \text{ hoặc } x- \frac{3}{2} = \frac{{ - 7}}{{12}}\\ x= \frac{7}{{12}} + \frac{3}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{ - 7}}{{12}} + \frac{3}{2}\\ x = \frac{{25}}{{12}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \frac{{11}}{{12}} \end{array}\)

\(\begin{array}{l} \frac{{81}}{{{3^{x + 1}}}} = 3\\ \frac{{{3^4}}}{{{3^{x + 1}}}} = 3\\ {3^{4 - \left( {x + 1} \right)}} = {3^1}\\ 4 - \left( {x + 1} \right) = 1\\ x + 1 = 4 - 1\\ x + 1 = 3\\ x = 2 \end{array}\)

Ta có

\(\begin{array}{l} \frac{{ - 1}}{8} \cdot \frac{5}{6} - \frac{1}{8} \cdot \frac{1}{6} + \frac{{{{( - 2020)}^0}}}{8}\\ = \frac{{ - 1}}{8} \cdot \frac{5}{6} + \frac{{ - 1}}{8} \cdot \frac{1}{6} + \frac{1}{8}\\ = \frac{{ - 1}}{8} \cdot \frac{5}{6} + \frac{{ - 1}}{8} \cdot \frac{1}{6} - \frac{{ - 1}}{8}\\ = \frac{{ - 1}}{8}.\left( {\frac{5}{6} + \frac{1}{6} - 1} \right) = \frac{{ - 1}}{8}.0 = 0 \end{array}\)

ÁP dụng tính chất dãy tỉ số bằng nhau ta có

\(\begin{array}{l} \frac{x}{4} = \frac{y}{{ - 5}}{\rm{ = }}\frac{{x - y}}{{4 - \left( { - 5} \right)}} = \frac{{ - 36}}{9} = - 4\\ \text{Với }\frac{x}{4} = - 4 \Rightarrow x = - 4.4 = - 16\\ \text{Với }\frac{y}{{ - 5}} = - 4 \Rightarrow x = \left( { - 4} \right).\left( { - 5} \right) = 20 \end{array}\)

Vậy x=-16, y=20

Ta có

\(\begin{array}{l} \frac{x}{y} = \frac{7}{{13}} \Rightarrow \frac{x}{7}{\rm{ = }}\frac{y}{{13}}\\ \Rightarrow \frac{{3.x}}{{3.7}}{\rm{ = }}\frac{{2.y}}{{2.13}} \Leftrightarrow \frac{{3x}}{{21}} = \frac{{2y}}{{26}} \end{array}\)

ÁP dụng tính chất dãy tỉ số bằng nhau ta có

\(\begin{array}{l} \frac{{3x}}{{21}} = \frac{{2y}}{{26}} = \frac{{3x - 2y}}{{21 - 26}} = \frac{{40}}{{ - 5}} = - 8\\ \frac{{3x}}{{21}} = - 8 \Leftrightarrow 3x = - 8.21 \Rightarrow 3x = - 168 \Rightarrow x = - 56\\ \frac{{2y}}{{26}} = - 8 \Leftrightarrow 2y = - 8.26 \Rightarrow 2y = - 208 \Rightarrow y = - 104 \end{array}\)

Vây x=-56, y=-104

Gọi x là chiều rộng hình chữ nhật (x>0)

Gọi y là chiều dài hình chữ nhật (y>0)

Theo đề bài ta có

\(x:y = 2:3 \Rightarrow \frac{x}{2} = \frac{y}{3}\)

Chu vi hình chữ nhật là 40 nên x+y=20.

Theo tính chất dãy tỉ số bằng nhau ta có

\(\begin{array}{l} \frac{x}{2} = \frac{y}{3} = \frac{{x + y}}{{2 + 3}} = \frac{{20}}{5} = 4\\ \text{Với }\frac{x}{2} = 4 \Rightarrow x = 4.2 = 8\\ \text{Với }\frac{y}{3} = 4 \Rightarrow y = 3.4 = 12 \end{array}\)

Vậy chiều rộng là 8cm, chiều dài là 12cm

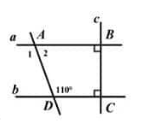
Ta có 

\(\begin{array}{l} \left. \begin{array}{l} a \bot c\\ b \bot c \end{array} \right\} \Rightarrow a//b\\ \left. \begin{array}{l} a//b\\ \widehat {{A_1}}\,\,và\,\,\widehat {ADC} \text{ nằm ở vị trí so le trong} \end{array} \right\} \Rightarrow \widehat {{A_1}} = \widehat {ADC} = {110^0} \end{array}\)

Ta có 

\(\begin{array}{l} \,\,\,\,\frac{x}{5} = \frac{{ - 2}}{{10}}\\ 10x = ( - 2).5\\ 10x = - 10\\ \,\,\,\,\,x = \left( { - 10} \right):10\\ \,\,\,\,\,x = - 1 \end{array}\)

Ta có 

\(\begin{array}{l} \frac{x}{2} = \frac{y}{5}{\rm{ }} \Leftrightarrow \frac{{x.x}}{2} = \frac{{x.y}}{5}\\ \Leftrightarrow \frac{{{x^2}}}{2} = \frac{{90}}{5}\\ \Leftrightarrow \frac{{{x^2}}}{2} = 18\\ \Leftrightarrow {x^2} = 36\\ \Leftrightarrow x = 6\text{ hoặc }x = - 6 \end{array}\)

Với \(x = 6 \Rightarrow 6.y = 90 \Rightarrow y = 15\)

Với \(x = -6 \Rightarrow -6.y = 90 \Rightarrow y = -15\)

\({\left( {\frac{3}{2}} \right)^4}.{\left( {\frac{3}{2}} \right)^6}={\left( {\frac{3}{2}} \right)^{4+6}}={\left( {\frac{3}{2}} \right)^{10}}\)

\(x^9.x^3.x=x^{9+3+1}=x^{13}\)

\(-\frac{9}{24}=-0,375\) nên \(-\frac{9}{24}\) được viết dưới dạng số thập phân hữu hạn.