Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Lạc Long Quân
Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Lạc Long Quân
-
Hocon247
-
40 câu hỏi
-
60 phút
-
95 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hỏi hàm số \(y=2 x^{4}-5\) đồng biến trên khoảng nào?
Ta có \(y^{\prime}=8 x^{3}, y^{\prime}>0 \Leftrightarrow x>0\)
Nên hàm số đã cho đồng biến trên \((0 ;+\infty)\)
Số điểm cực trị của hàm số \(y=-x^{3}+3 x^{2}+x+3\) là
\(y^{\prime}=-3 x^{2} +6 x+1\) có hai nghiệm phân biệt nên hàm số có hai điểm cực trị.
Tìm giá trị lớn nhất của hàm số \(y=-x^{3}+3 x^{2}\) trên đoạn [-3;1]
\(\begin{aligned} &y^{\prime}=-3 x^{2}+6 x=0 \Leftrightarrow x=0 \text { (thỏa mãn) hoặc } x=2 \text { (loại) }\\ &y(-3)=54 ; y(0)=0 ; y(1)=2\\ &\text {Vậy: } \max\limits _{[-3 ; 1]} y=54\end{aligned}\)
Đồ thị hàm số \(y=\frac{2 x+3}{x+2}\) có các đường tiệm cận là:
Nhắc lại đồ thị hàm số \(y=\frac{a x+b}{c x+d}\) có đường tiệm cận ngang là \(y=\frac{a}{c}\) và đường tiệm cận đứng là \(x=\frac{-d}{c}\) .
Vậy đồ thị hàm số có tiệm cận đứng là x=-2 và tiệm cận ngang y=2
Cho đồ thị như hình vẽ bên. Đây là đồ thị của hàm số nào?
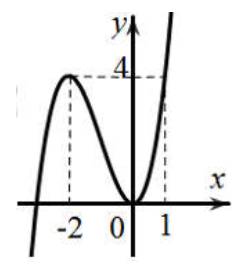
Khi x tiến tới \(+\infty\) thì y tiến tới \(+\infty\) , do đó hệ số của x3 phải dương nên loại B, C
Đồ thị hàm số đi qua điểm (0;0) nên hàm số ở ý D không thỏa mãn
Khi tăng độ dài tất cả các cạnh của một khối hộp chữ nhật lên gấp ba thì thể tích khối hộp tương ứng sẽ:
Giả sử chiều dài, chiều rộng, chiều cao của khối hộp chữ nhật là a, b, c .
Thể tích của khối hộp là V =abc .
Khi tăng tất cả các cạnh của khối hộp lên gấp đôi thì thể tích khối hộp thu được là
\(V^{\prime}=3 a \cdot 3 b \cdot 3 c=27 a b c=27 V\)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , \(A B=3 a, A C=4 a\) , SB vuông góc (ABC), \(S C= a\sqrt{41} \) . Tính thể tích khối chóp S.ABC theo a
Ta có \(S_{\Delta B C}=\frac{1}{2} \cdot A B \cdot A C=6a^2\)
\(BC = \sqrt {A{B^2} + A{C^2}} = 5a\)
\(S B=\sqrt{S C^{2}-B C^{2}}=4a\)
Vậy \(V_{S . A B C}=\frac{1}{3} \cdot S_{\triangle A B C} \cdot S B=8 a^{3}(\mathrm{dvtt})\)
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
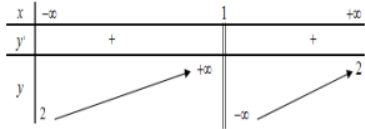
Dựa vào bảng biến thiên ta có hàm số f(x) đồng biến trên các khoảng \((-\infty ; 1) \text { và }(1 ;+\infty)\)
Cho hàm số y =f(x) có bảng biến thiên như sau:
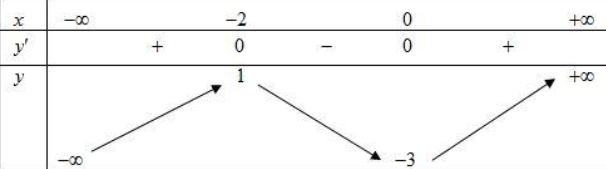
Hàm số y=f(x) nghịch biến trên khoảng nào dưới đây?
Dựa vào bản biến thiên, trên khoảng (-2;0) thì y'<0 nên hàm số nghịch biến trên khoảng (-2;0)
Cho hàm số\(y=f(x)\). Hàm số \(y=f'(x)\) có đồ thị như hình vẽ
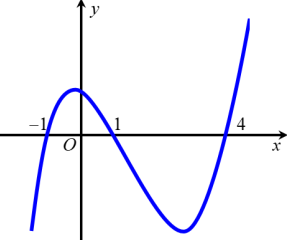
Hàm số \(y=f\left(2-e^{x}\right)\) đồng biến trên khoảng:
\(\begin{array}{l} \text { Ta có: } y=f\left(2-e^{x}\right) \Rightarrow y^{\prime}=-e^{x} f^{\prime}\left(2-e^{x}\right) \text { . } \\ f^{\prime}(x)=0 \Rightarrow\left[\begin{array}{l} 2-e^{x}=-1 \\ 2-e^{x}=1 \\ 2-e^{x}=4 \end{array} \Rightarrow\left[\begin{array}{l} x=\ln 3 \\ x=0 \\ e^{x}=-2(1) \end{array}\right.\right. \end{array}\)
Bảng xét dấu đạo hàm:
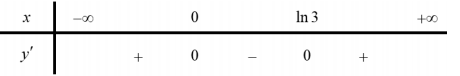
Vậy hàm số đồng biến trên các khoảng \((-\infty ; 0) ;(\ln 3 ;+\infty)\)
B thỏa
Cho hàm số \(y=x^{3}+17 x^{2}-24 x+8\). Kết luận nào sau đây là đúng?
\(y^{\prime}=3 x^{2}+34 x-24=0 \Leftrightarrow\left[\begin{array}{l} x=-12 \\ x=\frac{2}{3} \end{array}\right.\)
Lập bảng biến thiên ta thấy hàm số đạt cực đại tại x = −12 .
Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu?
Hàm số \(y=-10 x^{4}-5 x^{2}+7 \text { có } y^{\prime}=-40 x^{3}-10 x=0 \Leftrightarrow x=0 \text { và } y^{\prime \prime}(0)=-10<0\)
nên hàm số đạt cực đại tại x = 0
Cho hàm số y=f(x) có đạo hàm \(f^{\prime}(x)=(x+1)(x-2)^{2}(x-3)^{3}(x+5)^{4}\) . Hỏi hàm số y =f(x) có mấy điểm cực trị?
\(\begin{array}{l} {f^\prime }(x) = (x + 1){(x - 2)^2}{(x - 3)^3}{(x + 5)^4}\\ \Leftrightarrow \left[ \begin{array}{l} x + 1 = 0\\ {\left( {x - 2} \right)^2} = 0\\ {\left( {x - 3} \right)^3} = 0\\ {\left( {x + 5} \right)^4} = 0 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x = - 1\\ x = x\\ x = 3\\ x = - 5 \end{array} \right. \end{array}\)
Trong đó x=-1 và x=3 là các nghiệm bội lẻ nên y' đổi dấu khi đi qua x=-1 và x=3. Vậy x=-1 và x=3 là hai cực trị.
Qua các nghiệm bội chẵn x=2 và x=-5 thì y' không đổi dấu nên x=2 và c=-5 không phải cực trị.
Vậy hàm số có hai điểm cực trị.
Cho hàm số y =f(x) . Hàm số y = f'(x) có đồ thị như hình vẽ:
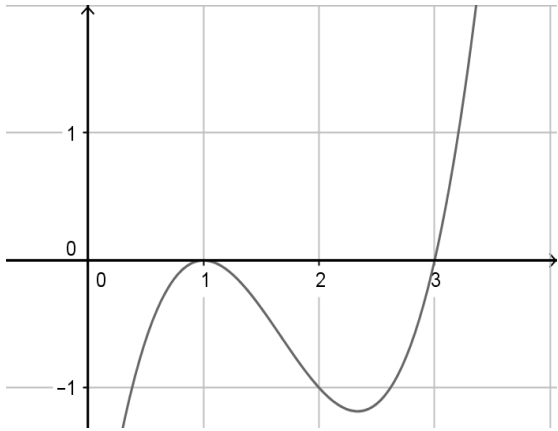
Khẳng định nào sau đây là khẳng định đúng?
Trên đồ thị hàm f'(x), khi đi qua x=3 thì y' đổi dấu từ âm sang dương nên x=3 là điểm cực tiểu của hàm số.
Qua x=1 thì y' không đổi sấu nên x=2 không phải cực trị.
Vậy đồ thị hàm số có 1 điểm cực tiểu.
Hàm số \(y=x^{3}-3 x^{2}+m x-2\) đạt cực tiểu tại x = 2 khi?
\(\begin{array}{l} y^{\prime}=3 x^{2}-6 x+m \\ y^{\prime \prime}=6 x-6 \end{array}\)
Hàm số đạt cực tiểu tại x = 2 khi:
\(\left\{\begin{array}{l} y^{\prime}(2)=3.2^{2}-6.2+m=0 \\ y^{\prime \prime}(2)=6.2-6>0 \end{array} \Leftrightarrow m=0\right.\)
Cho hàm số \(y=(m-1) x^{3}-3 x^{2}-(m+1) x+3 m^{2}-m+2\) . Để hàm số có cực đại, cực tiểu thì:
Hàm số có cực đại, cực tiểu khi \(\left\{\begin{array}{l} b^{2}-3 a c>0 \\ a \neq 0 \end{array} \Leftrightarrow\left\{\begin{array}{l} 9+3(m-1)(m+1)>0 \\ m-1 \neq 0 \end{array} \Leftrightarrow m \neq 1\right.\right.\)
Tìm tất cả các giá trị thực của m để hàm số \(y=m x^{4}-(m+1) x^{2}+2 m-1\) có 3 điểm cực trị ?
\(y^{\prime}=4 m x^{3}-2(m+1) x=0\)
\(\Leftrightarrow 2 x\left(2 m x^{2}-m-1\right)=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ 2 m x^{2}=m+1 \end{array}\right.\)
Hàm số có 3 điểm cực trị \(\Leftrightarrow m(m+1)>0 \Leftrightarrow\left[\begin{array}{l} m<-1 \\ m>0 \end{array}\right.\)
Tìm tất cả các giá trị thực của tham số m để hàm số: \(y=\frac{1}{3} x^{3}+m x^{2}+(m+6) x+m\) có cực đại và cực tiểu .
Ta có \(y^{\prime}=x^{2}+2 m x+m+6\)
Hàm số có cực đại, cực tiểu \(\Leftrightarrow y^{\prime}=0\) có hai nghiệm phân biệt.
\(\Leftrightarrow m^{2}-m-6>0 \Leftrightarrow\left[\begin{array}{l} m<-2 \\ m>3 \end{array}\right.\)
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y=\frac{x^{3}}{3}+2 x^{2}+3 x-4\) trên [-4;0] lần lượt là M và m . Giá trị của M + m bằng
Hàm số \(y=\frac{x^{3}}{3}+2 x^{2}+3 x-4\) xác định và liên tục trên [-4;0]
\(y^{\prime}=x^{2}+4 x+3, y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} x=-1(n) \\ x=-3(n) \end{array} \right.\\ f(0)=-4, f(-1)=-\frac{16}{3}, f(-3)=-4, f(-4)=-\frac{16}{3}\)
Vậy \(M=-4, m=-\frac{16}{3} \text { nên } M+m=-\frac{28}{3}\)
Đồ thị hàm số sau có bao nhiêu đường tiệm cận \(y=\frac{\sqrt{x-2}}{x^{2}-4 x+3} ?\)
TXĐ: \(D=[2 ;+\infty) \backslash\{3\}\)
\(\lim \limits_{x \rightarrow+\infty} \frac{\sqrt{x-2}}{x^{2}-4 x+3}=0 \Rightarrow\)
y=0 là tiệm cận ngang.
\(\lim _{x \rightarrow 3^{+}} \frac{\sqrt{x-2}}{x^{2}-4 x+3}=+\infty ; \lim _{x \rightarrow 3^{-}} \frac{\sqrt{x-2}}{x^{2}-4 x+3}=-\infty \Rightarrow\) x=3 là tiệm cận đứng.
vậy đồ thị hàm số có hai đường tiệm cận.
hàm số phù hợp với bảng biến thiên sau. Phát biểu nào sau đây là đúng

Dựa vào bảng biến thiên ta có: \(\lim \limits_{x \rightarrow+\infty} y=2 ; \lim\limits _{x \rightarrow-\infty} y=-1\) nên đồ thị hàm số có hai đường tiệm cận ngang là \(y=2 ; y=-1\)
Tìm phương trình tiệm cận đứng của đồ thị hàm số \(y=\frac{x-1}{x+1}\)
\(\mathrm{TXĐ}: D=\mathbb{R} \backslash\{-1\}\)
\(\lim _{x \rightarrow-1^{+}} y=\lim _{x \rightarrow-1^{+}} \frac{x-1}{x+1}=-\infty \Rightarrow x=-1\) là tiệm cận đứng của đồ thị hàm số.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a . Cạnh bên SA vuông góc với đáy và có độ dài bằng 2a . Thể tích khối tứ diện S.BCD là:
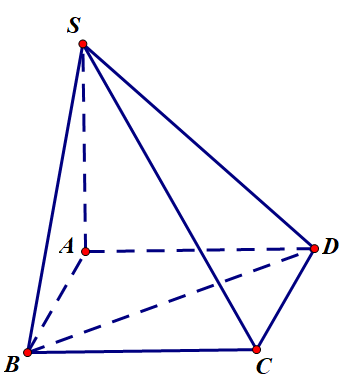
\(S_{\Delta B C D}=\frac{1}{2} S_{A B C D}=\frac{a^{2}}{2} . \text { Suy ra } V_{S . A B C D}=\frac{1}{3} S A . S_{\Delta B C D}=\frac{1}{3} \cdot 2 a \cdot \frac{a^{2}}{2}=\frac{a^{3}}{3}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a . Biết SA vuông góc với mặt phẳng đáy và \(S A=a \sqrt{2}\). Tính thể tích khối chóp S.ABO.
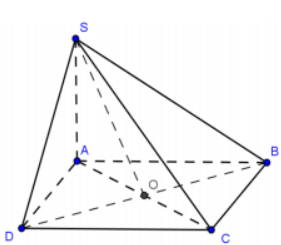
\(\begin{array}{l} \text { Ta có: } A C=2 a \cdot \sqrt{2} \Rightarrow O A=O B=\frac{A C}{2}=a \sqrt{2} \Rightarrow S_{O A B}=\frac{1}{2} O A \cdot O B=a^{2} \\ \text { Vậy }: V_{S . O A B}=\frac{1}{3} S A . S_{O A B}=\frac{1}{3} \cdot a \sqrt{2} \cdot a^{2}=\frac{\sqrt{2}}{3} \cdot a^{3} \end{array}\)
Cho hình chóp tam giác S.ABC với SA , SB , SC đôi một vuông góc và \(S A=S B=S C=a\) . Tính thế tích của khối chóp S.ABC.
Ta có \(V=\frac{1}{3} \cdot S_{S B C} \cdot S A=\frac{1}{3} \cdot \frac{1}{2} \cdot S B \cdot S C \cdot S A=\frac{1}{6} \cdot a^{3}\)
Cho hình chóp S.ABCD đáy ABCD là hình vuông có cạnh a và SA vuông góc đáy ABCD và mặt bên (SCD) hợp với đáy một góc 600. Tính thể tích hình chóp S ABCD . .
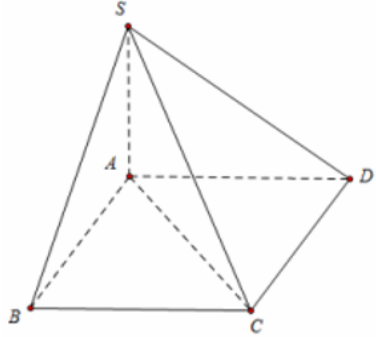
\(\begin{array}{l} \text { Do }\left\{\begin{array}{l} A D \perp C D \\ S A \perp C D \end{array} \Rightarrow C D \perp(S D A) \Rightarrow(S C D),(A B C)=\widehat{S D A}\right. \\ \text { Khi đó } S A=A D \tan 60^{\circ}=a \sqrt{3} \\ \text { Suy ra } V_{S . A B C D}=\frac{1}{3} S A \cdot S_{A B C D}=\frac{a^{3} \sqrt{3}}{3} \end{array}\)
Với giá trị nào của thì đẳng thức \(\sqrt[2016]{x^{2016}}=-x\) đúng
Do \(\sqrt[2016]{x^{2016}}=|x| \text { nên } \sqrt[2016]{x^{2016}}=-x \Leftrightarrow|x|=-x \text { khi } x \leq 0\)
Căn bậc 4 của 3 là
Theo định nghĩa căn bậc n của số b : Cho số thực n và số nguyên dương b \((n \geq 2)\) .
Số a được gọi là căn bậc n của số b nếu \(a^{n}=b\)
Nếu n chẵn và b>0 Có hai căn trái dấu, kí hiệu giá trị dương là \(\sqrt[n]{b}\) , còn giá trị âm kí hiệu là \(-\sqrt[n]{b}\) . Nên có hai căn bậc 4 của 3 là \(\pm \sqrt[4]{3}\)
Với giá trị nào của thì biểu thức \(\left(4-x^{2}\right)^{\frac{1}{3}}\) có nghĩa
ĐKXĐ: \(4-x^{2}>0 \Leftrightarrow-2<x<2\)
So sánh hai số m và n nếu \(3,2^{m}<3,2^{n}\) thì:
\(\text { Do } 3,2>1 \text { nên } 3,2^{m}<3,2^{n} \Leftrightarrow m<n\)
Cho \(a=1+2^{-x}, b=1+2^{x}\) . Biểu thức biểu diễn b theo a là:
\(\begin{aligned} &\text { Ta có: } a=1+2^{-x}>1, \forall x \in \mathbb{R} \text { nên } 2^{x}=\frac{1}{a-1}\\ &\text { Do đó: } b=1+\frac{1}{a-1}=\frac{a}{a-1} \end{aligned}\)
Tập xác định của hàm số \(y=\log _{0,5}(x+1)\) là:
ĐKXĐ: \(x+1>0 \Leftrightarrow x>-1\)
Cho hàm số \(y=3^{\frac{x}{2}}\)có đồ thị (C). Hàm số nào sau đây có đồ thị đối xứng với qua đường thẳng y=x
Ta có \(y=3^{\frac{x}{2}}=(\sqrt{3})^{x}\)
dựa vào lý thuyết Hai hàm số \(y=a^{x} \text { và } y=\log _{a} x\) có đồ thị đối xứng nhau qua đường phân giác của góc phần tư thứ nhất y=x ''
Vậy chọn A
Phương trình \(3^{x^{3}-9 x+4}=81\) có mấy nghiệm?
Ta có \(3^{x^{3}-9 x+4}=81=3^{4} \Leftrightarrow x^{3}-9 x+4=4 \Leftrightarrow x\left(x^{2}-9\right)=0 \Leftrightarrow x \in\{0 ;\pm 3\}\)
Vậy phương trình có 3 nghiệm.
Cho phương trình \(4.4^{x}-9.2^{x+1}+8=0\) . Gọi \(x_1; x_2\) là hai nghiệm của phương trình trên. Khi đó, tích \(x_1. x_2\) bằng:
Đặt \(t=2^{x}(t>0)\), khi đó phương trình đã cho tương đương với
\(4 t^{2}-18 t+8=0 \Leftrightarrow\left[\begin{array}{l} t=4 \\ t=\frac{1}{2} \end{array} \Leftrightarrow\left[\begin{array}{l} x_{1}=2 \\ x_{2}=-1 \end{array}\right.\right.\)
Vậy \(x_{1} \cdot x_{2}=-1.2=-2\)
Tổng các nghiệm không âm của phương trình \(\log _{\sqrt{3}} x-\log _{3}\left(2 x^{2}-4 x+3\right)=0\) là:
\(\begin{aligned} &\text { Điều kiện } x>0\\ &\log _{\sqrt{3}} x-\log _{3}\left(2 x^{2}-4 x+3\right)=0 \Leftrightarrow 2 \log _{3} x-\log _{3}\left(2 x^{2}-4 x+3\right)=0 \Leftrightarrow \log _{3} x^{2}=\log _{3}\left(2 x^{2}-4 x+3\right)\\ &\Leftrightarrow x^{2}=2 x^{2}-4 x+3 \Leftrightarrow x^{2}-4 x+3=0 \Leftrightarrow\left[\begin{array}{l} x_{1}=1 \\ x_{2}=3 \end{array} \Rightarrow x_{1}+x_{2}=4\right. \end{aligned}\)
Với giá trị m bằng bao nhiêu thì phương trình \(\log _{2+\sqrt{3}}(m x+3)+\log _{2-\sqrt{3}}\left(m^{2}+1\right)=0\) có nghiệm là -1 ?
Thay x =-1vào phương trình ta có
\(\begin{array}{l} \log _{2+\sqrt{3}}(-m+3)+\log _{2-\sqrt{3}}\left(m^{2}+1\right)=0 \Leftrightarrow \log _{2+\sqrt{3}}(-m+3)+\log _{(2+\sqrt{3})^{-1}}\left(m^{2}+1\right)=0 \\ \Leftrightarrow \log _{2+\sqrt{3}}(-m+3)-\log _{(2+\sqrt{3})}\left(m^{2}+1\right)=0 \Leftrightarrow \log _{2+\sqrt{3}}(-m+3)=\log _{(2+\sqrt{3})}\left(m^{2}+1\right) \\ \Leftrightarrow-m+3=m^{2}+1 \Leftrightarrow m^{2}+m-2=0 \Leftrightarrow\left[\begin{array}{l} m=1 \\ m=-2 \end{array}\right. \end{array}\)
Trong không gian Oxyz, cho \(A(1 ; 0 ; 1), B(0;1;-1)\). Tính độ dài AB
\(AB=\sqrt {(x_A-x_B)^2+(y_A-y_B)^2+(y_A-y_B)^2}=\sqrt {1+1+1}=\sqrt 3\)
Tập nghiệm của phương trìnhlog \(\log _{\sqrt{3}}|x-1|=2\) là:
\(\log _{\sqrt{3}}|x-1|=2 \Leftrightarrow|x-1|=3 \Leftrightarrow\left[\begin{array}{l} x=4 \\ x=-2 \end{array}\right.\)