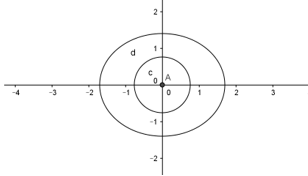
Người ta cần trồng hoa tại phần đắt nằm phía ngoài đường tròn tâm gốc tọa độ $O$ , bán kính bằng \(\dfrac{1}{{\sqrt 2 }}\) và phía trong của Elip có độ dài trục lớn bằng \(2\sqrt 2 \) và độ dài trục nhỏ bằng $2$ (như hình vẽ bên). Trong mỗi một đơn vị diện tích cần bón \(\dfrac{{100}}{{(2\sqrt 2  - 1)\pi }}kg\) phân hữu cơ. Hỏi cần sử dụng bao nhiêu kg phân hữu cơ để bón cho hoa?

 Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y=x{{e}^{x}},\ \ y=0,\ x=0,\ x=1\) xung quanh trục \(Ox\) là:  

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm

$A\left( {1;2; - 1} \right),{\rm{ }}B\left( {2;1;1} \right),{\rm{ }}C\left( {0;1;2} \right)$. Gọi $H\left( {a;b;c} \right)$ là trực tâm của tam giác \(ABC\). Giá trị của $a + b + c$ bằng:

Trong không gian Oxyz, cho các điểm \(A\left( 2;-2;\ 1 \right),\ B\left( 1;-1;\ 3 \right).\) Tọa độ của vecto \(\overrightarrow{AB}\) là

Cho số phức \(z\) thỏa mãn\(|z - 1 - 2i| = 4\). Gọi $M,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của \(|z + 2 + i|\). Tính \(S = {M^2} + {m^2}\).

Cho phương trình $4{z^4} + m{z^2} + 4 = 0$ trong tập số phức và \(m\) là tham số thực. Gọi \({z_1},{\rm{ }}{z_2},{\rm{ }}{z_3},{\rm{ }}{z_4}\) là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của \(m\) để \(\left( {z_1^2 + 4} \right)\left( {z_2^2 + 4} \right)\left( {z_3^2 + 4} \right)\left( {z_4^2 + 4} \right) = 324\).

Cho ba điểm $A,B,C$ lần lượt biểu diễn các số phức sau \({z_1} = 1 + i;\,{z_2} = {z_1}^2;\,{z_3} = m - i\). Tìm các giá trị thực của $m$ sao cho tam giác $ABC$ vuông tại $B$.

Gọi \(S\) là tổng phần thực và phần ảo của số phức $w = {z^3} - i$, biết $z$ thỏa mãn $z + 2 - 4i = \left( {2 - i} \right)\overline {iz} $. Mệnh đề nào sau đây đúng?

Trong không gian với hệ tọa độ \(Oxyz,\) cho các điểm \(A\left( -\,1;1;1 \right),\,\,B\left( 1;0;1 \right).\) Mặt phẳng \(\left( P \right)\) đi qua \(A,\,\,B\) và \(\left( P \right)\) cách điểm \(O\) một khoảng lớn nhất. Phương trình của mặt phẳng \(\left( P \right)\) là

Trong không gian với hệ tọa độ vuông góc $Oxyz$, cho hai điểm $E\left( {2,1,1} \right),{\rm{ }}F\left( {0,3, - 1} \right)$. Mặt cầu $\left( S \right)$ đường kính $EF$ có phương trình là:

Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn \([0;\pi ]\) đạt giá trị bằng \(0\) ?

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} + 2x - 4y + 6z + 5 = 0$. Tiếp diện của $(S)$ tại điểm $M(-1;2;0)$ có phương trình là:

 Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y={{x}^{2}}-4x+4\), trục tung và trục hoành. Xác định k để đường thẳng (d) đi qua điểm \(A\left( 0;4 \right)\) và có hệ số góc k chia (H) thành hai phần có diện tích bằng nhau.

Trong không gian với hệ tọa độ \(Oxyz\), cho \(d\) là đường thẳng đi qua gốc tọa độ \(O\), vuông góc với trục \(Ox\) và vuông góc với đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 1 - 3t\end{array} \right.\). Phương trình của \(d\) là:

Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = x{e^x}\) , trục hoành, hai đường thẳng \(x =  - 2;x = 3\) có công thức tính là

Cho hình lập phương \(A\left( {0;0;0} \right),B\left( {1;0;0} \right),D\left( {0;1;0} \right),A'\left( {0;0;1} \right)\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,CD\). Khoảng cách giữa \(MN\) và \(A'C\) là: