Cho tứ diện \(ABCD\) có \(AB = a;\)\(AC = BC = AD = BD = \dfrac{{a\sqrt 3 }}{2}\). Gọi \(M,\,\,N\) là trung điểm của \(AB,\,\,CD\). Góc giữa hai mặt phẳng \(\left( {ABD} \right);\,\,\left( {ABC} \right)\) là \(\alpha \) . Tính \({\rm{cos}}\alpha \) biết mặt cầu đường kính \(MN\) tiếp xúc với cạnh \(AD\).
A.
\(2 - \sqrt 3 \)
B.
\(2\sqrt 3 - 3\)
C.
\(3 - 2\sqrt 3 \)
D.
\(\sqrt 2 - 1\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: b
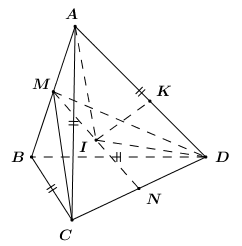
Xét các tam giác ACB, ADB lần lượt cân tại C và D nên \(CM \bot AB,DM \bot AB\)
Ta có : \(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABD} \right) = AB\\CM \bot AB,CM \subset \left( {ABC} \right)\\DM \bot AB,DM \subset \left( {ABD} \right)\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABD} \right)} \right) = \angle \left( {CM;DM} \right)\).
Tam giác ACM vuông tại M nên theo Pitago ta có :
\(\begin{array}{l}C{M^2} = A{C^2} - A{M^2}\\ \Rightarrow CM = \sqrt {A{C^2} - A{M^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\end{array}\)
Tương tự \(DM = \dfrac{{a\sqrt 2 }}{2}\).
Gọi K là hình chiếu của I lên AD ta có :
Mặt cầu đường kính MN tiếp xúc với AD nên \(IK = IM = IN,IK \bot AD\).
Xét tam giác AMI và AKI có :
\(\begin{array}{l}\widehat {AMI} = \widehat {AKI} = {90^0};\\AI\,chung;\\IM = IK\left( {cmt} \right);\end{array}\)
Do đó \(\Delta AMI = \Delta AKI\) (cạnh huyền – cạnh góc vuông) \( \Rightarrow AK = AM = \dfrac{a}{2}\) (cạnh tương ứng).
Tương tự : \(\Delta DNI = \Delta DKI\) (cạnh huyền – cạnh góc vuông)
\(\begin{array}{l} \Rightarrow DN = DK = AD - AK = \dfrac{{a\sqrt 3 }}{2} - \dfrac{a}{2} = \dfrac{{a\left( {\sqrt 3 - 1} \right)}}{2}\\ \Rightarrow DC = 2DN = 2.\dfrac{{a\left( {\sqrt 3 - 1} \right)}}{2} = a\left( {\sqrt 3 - 1} \right)\end{array}\)
Ap dụng định lý cô sin trong tam giác MCD có :
\(\begin{array}{l}\cos \widehat {CMD} = \dfrac{{M{C^2} + M{D^2} - C{D^2}}}{{2MC.MD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} - {{\left( {a\left( {\sqrt 3 - 1} \right)} \right)}^2}}}{{2.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{a\sqrt 2 }}{2}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\sqrt 3 - 3 > 0\\ \Rightarrow \cos \alpha = \cos \widehat {CMD} = 2\sqrt 3 - 3\end{array}\)
Hướng dẫn giải:
- Xác định góc \(\alpha \): Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến.
- Tính \(\cos \alpha \) bằng cách sử dụng định lý cô sin trong tam giác: \(\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\).

Xét các tam giác ACB, ADB lần lượt cân tại C và D nên \(CM \bot AB,DM \bot AB\)
Ta có : \(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABD} \right) = AB\\CM \bot AB,CM \subset \left( {ABC} \right)\\DM \bot AB,DM \subset \left( {ABD} \right)\end{array} \right.\)\( \Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABD} \right)} \right) = \angle \left( {CM;DM} \right)\).
Tam giác ACM vuông tại M nên theo Pitago ta có :
\(\begin{array}{l}C{M^2} = A{C^2} - A{M^2}\\ \Rightarrow CM = \sqrt {A{C^2} - A{M^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 2 }}{2}\end{array}\)
Tương tự \(DM = \dfrac{{a\sqrt 2 }}{2}\).
Gọi K là hình chiếu của I lên AD ta có :
Mặt cầu đường kính MN tiếp xúc với AD nên \(IK = IM = IN,IK \bot AD\).
Xét tam giác AMI và AKI có :
\(\begin{array}{l}\widehat {AMI} = \widehat {AKI} = {90^0};\\AI\,chung;\\IM = IK\left( {cmt} \right);\end{array}\)
Do đó \(\Delta AMI = \Delta AKI\) (cạnh huyền – cạnh góc vuông) \( \Rightarrow AK = AM = \dfrac{a}{2}\) (cạnh tương ứng).
Tương tự : \(\Delta DNI = \Delta DKI\) (cạnh huyền – cạnh góc vuông)
\(\begin{array}{l} \Rightarrow DN = DK = AD - AK = \dfrac{{a\sqrt 3 }}{2} - \dfrac{a}{2} = \dfrac{{a\left( {\sqrt 3 - 1} \right)}}{2}\\ \Rightarrow DC = 2DN = 2.\dfrac{{a\left( {\sqrt 3 - 1} \right)}}{2} = a\left( {\sqrt 3 - 1} \right)\end{array}\)
Ap dụng định lý cô sin trong tam giác MCD có :
\(\begin{array}{l}\cos \widehat {CMD} = \dfrac{{M{C^2} + M{D^2} - C{D^2}}}{{2MC.MD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} - {{\left( {a\left( {\sqrt 3 - 1} \right)} \right)}^2}}}{{2.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{a\sqrt 2 }}{2}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\sqrt 3 - 3 > 0\\ \Rightarrow \cos \alpha = \cos \widehat {CMD} = 2\sqrt 3 - 3\end{array}\)
Hướng dẫn giải:
- Xác định góc \(\alpha \): Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến.
- Tính \(\cos \alpha \) bằng cách sử dụng định lý cô sin trong tam giác: \(\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\).
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hình nón có độ dài đường sinh bằng 5, bán kính bằng 3. Diện tích toàn phần của hình nón bằng:
Cho các hình sau đây: điểm, đường thẳng, đường tròn. Số hình khi quay quanh một trục cố định ta được mặt tròn xoay là:
Cần đẽo thanh gỗ hình hộp có đáy là hình vuông thành hình trụ có cùng chiều cao. Tỉ lệ thể tích gỗ cần phải đẽo đi ít nhất (tính gần đúng) là
Cho khối nón có độ dài đường sinh bằng \(2a\) và bán kính đáy bằng \(a\). Thể tích của khối nón đã cho bằng
Cho mặt cầu \(S\left( {I;R} \right)\) và mặt phẳng \(\left( P \right)\) cách I một khoảng bằng \(\frac{R}{2}\). Khi đó giao của \(\left( P \right)\) và \(\left( S \right)\) là đường tròn có chu vi bằng:
Cho hình nón đỉnh $S$, tâm đáy là $O$, góc ở đỉnh là ${135^0}$. Trên đường tròn đáy lấy điểm $A$ cố định và điểm $M$ di động. Tìm số vị trí $M$ để diện tích $SAM$ đạt giá trị lớn nhất
Cho ba hình cầu có bán kính lần lượt là \({R_1},{R_2},{R_3}\) đôi một tiếp xúc nhau và cùng tiếp xúc với mặt phẳng (P). Các tiếp điểm của ba hình cầu với mặt phẳng (P) lập thành một tam giác có độ dài cạnh lần lượt là 2, 3, 4. Tính tổng \({R_1} + {R_2} + {R_3}\):
Hình trụ có bán kính \(r = 5cm\) và chiều cao \(h = 3cm\) có diện tích toàn phần gần với số nào sau đây?
Nếu cắt mặt trụ tròn xoay bởi một mặt phẳng tạo với trục một góc \(\alpha \left( {{0^0} < \alpha < {{90}^0}} \right)\) thì ta được:
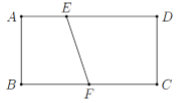
Có một miếng bìa hình chữ nhật \(ABCD\) với \(AB = 3\) và \(AD = 6\). Trên cạnh \(AD\) lấy điểm \(E\) sao cho \(AE = 2\), trên cạnh \(BC\) lấy điểm \(F\) là trung điểm của \(BC\). Cuốn miếng bìa lại sao cho \(AB\) trùng \(DC\)để tạo thành mặt xung quanh của một hình trụ.
Khi đó tính thể tích \(V\) của tứ diện \(ABEF\).
Nếu tăng bán kính của mặt cầu lên 4 lần thì diện tích mặt cầu tăng lên bao nhiêu lần?
Tính thể tích \(V\) của khối trụ ngoại tiếp hình lập phương có cạnh bằng $a$.
Số giao điểm của đường thẳng và mặt cầu tối đa có thể có là:
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AA’ = 2a, BC = a. Gọi M là trung điểm BB’. Bán kính mặt cầu ngoại tiếp khối chóp M.A’B’C’ bằng:
Quay hình chữ nhật \(ABCD\) quanh mỗi cạnh \(AB,CD\) thì ta được hai hình trụ có

