Cho tam giác $ABO$ vuông tại $O$, có góc \(\widehat {BAO} = {30^0},AB = a\) . Quay tam giác $ABO$ quanh trục $AO$ ta được một hình nón có diện tích xung quanh bằng:
A.
\(\dfrac{{\pi {a^2}\sqrt 3 }}{4}\).
B.
\(2\pi {a^2}\).
C.
\(\dfrac{{\pi {a^2}}}{2}\)
D.
\(\dfrac{{\pi {a^2}}}{4}\).
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
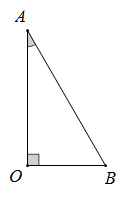
Hình nón thu được có đường sinh $l = AB = a$; bán kính đáy
$r = OB = AB.\sin 30^\circ = \dfrac{a}{2}$ và diện tích xung quanh là
${S_{xq}} = \pi rl = \dfrac{{\pi {a^2}}}{2}$
Hướng dẫn giải:
Công thức tính diện tích xung quanh \({S_{xq}} = \pi rl\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án A vì áp dụng nhầm công thức \({S_{xq}} = \pi rh\).

Hình nón thu được có đường sinh $l = AB = a$; bán kính đáy
$r = OB = AB.\sin 30^\circ = \dfrac{a}{2}$ và diện tích xung quanh là
${S_{xq}} = \pi rl = \dfrac{{\pi {a^2}}}{2}$
Hướng dẫn giải:
Công thức tính diện tích xung quanh \({S_{xq}} = \pi rl\).
Giải thích thêm:
Một số em sẽ chọn nhầm đáp án A vì áp dụng nhầm công thức \({S_{xq}} = \pi rh\).
CÂU HỎI CÙNG CHỦ ĐỀ
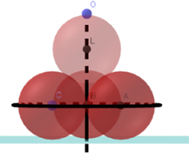
Có 4 viên bi hình cầu bán kính bằng 1cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đai 3 viên bi đó lại và đặt 1 viên bi thứ 4 tiếp xúc vởi cả 3 viên bi trên như hình vẽ bên dưới. Gọi O là điểm thuộc bề mặt của viên bi thứ 4 có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng
Một cái cốc hình trụ cao $15cm$ đựng được $0,5$ lít nước. Hỏi bán kính đường tròn đáy đáy của cốc xấp xỉ bằng bao nhiêu (làm tròn đến hàng thập phân thứ hai)?
Cho một mặt cầu bán kính bằng $1$. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
Cho hình trụ có các đáy là hình tròn tâm $O$ và tâm $O'$ , bán kính đáy bằng chiều cao và bằng $4cm$. Trên đường tròn đáy tâm $O$ lấy điểm $A$, trên đường tròn đáy tâm $O'$ lấy điểm B sao cho $AB = 4\sqrt 3 cm$. Thể tích khối tứ diện $AOO'B$ là:
Các tiếp tuyến tại cùng một điểm nằm trên mặt cầu có tính chất:
Cho lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác vuông cân đỉnh $A,AB = AC = a,AA' = a\sqrt 2 $. Diện tích mặt cầu ngoại tiếp tứ diện $CA'B'C'$ là:
Diện tích xung quanh hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(4cm\) là:
Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng $1, 2, 4.$ Tổng độ dài đường kính của hai quả bóng đó.
Cho hình chữ nhật \(ABCD\), khi quay hình chữ nhật quanh cạnh \(AD\) thì \(CD\) được gọi là:
Thể tích khối nón có bán kính đáy \(r = 2cm\) và \(h = 3cm\) là:
Cho tam giác $AOB$ vuông tại $O$. Quay tam giác quanh cạnh $OA$ ta được hình nón có đường sinh và đường cao lần lượt là:
Cho mặt cầu \(\left( S \right)\) tâm \(O\), bán kính \(R\) và mặt phẳng \(\left( P \right)\), gọi \(H\) là hình chiếu của \(O\) trên \(\left( P \right)\). Nếu \(R > OH\) thì:
Cho hình chóp đều $n$ cạnh $(n \ge 3)$. Cho biết bán kính đường tròn ngoại tiếp đa giác đáy là $R$ và góc giữa mặt bên và mặt đáy bằng ${60^0}$ , thể tích khối chóp bằng $\dfrac{{3\sqrt 3 }}{4}{R^3}$ . Tìm $n$?
Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ đó bằng $V$ và diện tích toàn phần phần hình trụ nhỏ nhất thì bán kính đáy $R$ bằng:

