Cho hình chóp $S.ABC$ có $SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha $. Gọi $B',C'$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính bán kính mặt cầu ngoại tiếp khối chóp $A.{\rm{ }}BCC'B'$ theo $b,c,\alpha $
A.
\(R = 2\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } \)
B.
\(R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{\sin 2\alpha }}\)
C.
$R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{2\sin \alpha }}$
D.
$R = \dfrac{{2\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{\sin \alpha }}$
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
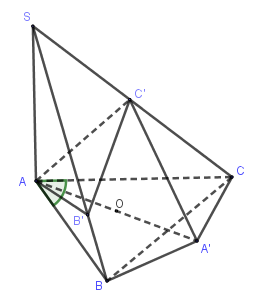
Gọi $AA'$ là đường kính của đường tròn ngoại tiếp tam giác $ABC$
\(AC \bot A'C;\,AB \bot A'B\)
Ta chứng minh \(AC' \bot A'C'\)
\(SA \bot A'C;\,AC \bot A'C \Rightarrow A'C \bot AC'\)
Mà \(AC' \bot SC \Rightarrow AC' \bot A'C'\)
Tương tự \(AB' \bot A'B'\)
Như vậy $B,C,C',B'$ cùng nhìn $AA'$ bằng $1$ góc vuông nên $A,B,C,B',C'$ cùng thuộc $1$ mặt cầu có đường kính là $AA'$ và cũng đồng thời là đường kính của đường tròn ngoại tiếp tam giác $ABC$.
Tính \(BC = \sqrt {{b^2} + {c^2} - 2b\cos \alpha } \)
Trong tam giác \(ABC:\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{2\sin \alpha }}\)
Hướng dẫn giải:
+ Chứng minh được tâm mặt cầu ngoại tiếp của hình chóp $ABCC'B'$ trùng với tâm đường tròn ngoại tiếp của tam giác

Gọi $AA'$ là đường kính của đường tròn ngoại tiếp tam giác $ABC$
\(AC \bot A'C;\,AB \bot A'B\)
Ta chứng minh \(AC' \bot A'C'\)
\(SA \bot A'C;\,AC \bot A'C \Rightarrow A'C \bot AC'\)
Mà \(AC' \bot SC \Rightarrow AC' \bot A'C'\)
Tương tự \(AB' \bot A'B'\)
Như vậy $B,C,C',B'$ cùng nhìn $AA'$ bằng $1$ góc vuông nên $A,B,C,B',C'$ cùng thuộc $1$ mặt cầu có đường kính là $AA'$ và cũng đồng thời là đường kính của đường tròn ngoại tiếp tam giác $ABC$.
Tính \(BC = \sqrt {{b^2} + {c^2} - 2b\cos \alpha } \)
Trong tam giác \(ABC:\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{2\sin \alpha }}\)
Hướng dẫn giải:
+ Chứng minh được tâm mặt cầu ngoại tiếp của hình chóp $ABCC'B'$ trùng với tâm đường tròn ngoại tiếp của tam giác
CÂU HỎI CÙNG CHỦ ĐỀ
Anh A mua 1 chiếc Laptop giá $23$ triệu đồng theo hình thức trả góp, lãi suất mỗi tháng là $0,5\% $. Hỏi mỗi tháng anh A phải trả cho cửa hàng bao nhiêu tiền để sau $6$ tháng anh trả hết nợ?
Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng \((P):x - y - z - 1 = 0\) và đường thẳng $d:\dfrac{{x + 1}}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{3}$. Phương trình đường thẳng \(\Delta \) qua \(A(1;1; - 2)\) vuông góc với $d$ và song song với $(P)$ là:
Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(M\left( 1;2;3 \right).\) Mặt phẳng \(\left( P \right)\) đi qua M và cắt các tia \(Ox;\,\,Oy;\,\,Oz\) lần lượt tại các điểm \(A;\,\,B;\,\,C\) \(\left( A;\,\,B;\,\,C\ne O \right)\) sao cho thể tích của tứ diện \(OABC\) nhỏ nhất. Phương trình của mặt phẳng \(\left( P \right)\) là
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} - 2{\rm{x + 4y - 4z - m = 0}}$ có bán kính $R = 5$. Tìm giá trị của $m$?
Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$, góc giữa cạnh bên và mặt đáy bằng \({60^0}\). Tính thể tích khối chóp $S.ABC$?
Cho ba điểm $A,B,C$ lần lượt biểu diễn các số phức sau \({z_1} = 1 + i;\,{z_2} = {z_1}^2;\,{z_3} = m - i\). Tìm các giá trị thực của $m$ sao cho tam giác $ABC$ vuông tại $B$.
Khoảng cách từ điểm \(M\left( {2;0;1} \right)\) đến đường thẳng $\Delta :\dfrac{{x - 1}}{1} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}$ là:
Trong không gian $Oxyz$ cho ba vecto \(\vec a = \left( { - 1;1;0} \right),\vec b = \left( {1;1;0} \right),\vec c = \left( {1;1;1} \right)\). Mệnh đề nào dưới đây sai?
Cho hình lăng trụ $ABC.A’B’C’$ có độ dài tất cả các cạnh bằng $a$ và hình chiếu vuông góc của đỉnh $C$ trên $(ABB’A’)$ là tâm của hình bình hành $ABB’A’$. Thể tích của khối lăng trụ là:
Cho hàm số $y = \dfrac{{x - 2}}{{{x^2} - 2x + m}}\left( C \right).$ Tất cả các giá trị của m để (C) có 3 đường tiệm cận là:
Hãy chọn cụm từ (hoặc từ) cho dưới đây để sau khi điền nó vào chỗ trống mệnh đề sau trở thành mệnh đề đúng:
“Số cạnh của một hình đa diện luôn……………….số mặt của hình đa diện ấy”
Thể tích vật thể tròn xoay sinh ra khi quay hình phẳng giới hạn bới các đường \(x=\sqrt{y};\,y=-x+2,x=0\) quanh trục $Ox$ có giá trị là kết quả nào sau đây ?
Nếu đặt $\left\{ \begin{array}{l}u = \ln \left( {x + 2} \right)\\{\rm{d}}v = x\,{\rm{d}}x\end{array} \right.$ thì tích phân $I = \int\limits_0^1 {x.\ln \left( {x + 2} \right){\rm{d}}x} $ trở thành
Trong không gian với hệ tọa độ $Oxyz$, cho ba vectơ $\vec a = \left( {1;m;2} \right),\vec b = \left( {m + 1;2;1} \right)$ và \(\vec c = \left( {0;m - 2;2} \right)\). Giá trị \(m\) bằng bao nhiêu để ba vectơ \(\vec a,\vec b,\vec c\) đồng phẳng
Cho hàm số $f\left( x \right)$ liên tục trên $R$ và $\int\limits_{ - 2}^4 {f\left( x \right)} dx{\rm{ = 2}}$ . Mệnh đề nào sau đây là sai?

