Cho hàm số \(f\left( x \right) = {\left( {{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} + {8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} + 1} \right)^{\dfrac{1}{2}}} - 1\) với \(0 < x \ne 1\). Tính giá trị biểu thức \(P = f\left( {f\left( {2018} \right)} \right)\).
A.
\(P = 2016\)
B.
\(P = 1009\)
C.
\(P = 2018\)
D.
\(P = {2018^2}\)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Đáp án đúng: c
Ta có:
\(\begin{array}{l}{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} = {x^{1 + \dfrac{1}{{{{\log }_2}x}}}} = {x^{1 + {{\log }_x}2}} = {x^{{{\log }_x}2x}} = 2x\\{8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{3.\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{\dfrac{1}{{{{\log }_{{x^2}}}2}}}} = {2^{{{\log }_2}{x^2}}} = {x^2}\end{array}\)
Khi đó \(f\left( x \right) = {\left( {{x^2} + 2x + 1} \right)^{\dfrac{1}{2}}} - 1 = {\left( {{{\left( {x + 1} \right)}^2}} \right)^{\dfrac{1}{2}}} - 1 = x \Rightarrow f\left( x \right) = x\)
Do đó \(P = f\left( {f\left( {2018} \right)} \right) = f\left( {2018} \right) = 2018\).
Hướng dẫn giải:
Sử dụng các công thức biến đổi logarit \({\log _a}{a^n} = n;{\log _a}b = \dfrac{1}{{{{\log }_b}a}};{a^{{{\log }_a}b}} = b\)
Ta có:
\(\begin{array}{l}{x^{1 + \dfrac{1}{{2{{\log }_4}x}}}} = {x^{1 + \dfrac{1}{{{{\log }_2}x}}}} = {x^{1 + {{\log }_x}2}} = {x^{{{\log }_x}2x}} = 2x\\{8^{\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{3.\dfrac{1}{{3{{\log }_{{x^2}}}2}}}} = {2^{\dfrac{1}{{{{\log }_{{x^2}}}2}}}} = {2^{{{\log }_2}{x^2}}} = {x^2}\end{array}\)
Khi đó \(f\left( x \right) = {\left( {{x^2} + 2x + 1} \right)^{\dfrac{1}{2}}} - 1 = {\left( {{{\left( {x + 1} \right)}^2}} \right)^{\dfrac{1}{2}}} - 1 = x \Rightarrow f\left( x \right) = x\)
Do đó \(P = f\left( {f\left( {2018} \right)} \right) = f\left( {2018} \right) = 2018\).
Hướng dẫn giải:
Sử dụng các công thức biến đổi logarit \({\log _a}{a^n} = n;{\log _a}b = \dfrac{1}{{{{\log }_b}a}};{a^{{{\log }_a}b}} = b\)
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số \(y = \dfrac{{x + b}}{{cx - 1}}\) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

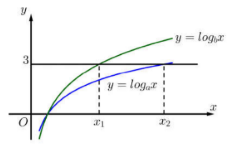
Hàm số \(y = {\log _a}x\) và \(y = {\log _b}x\) có đồ thị như hình vẽ bên:
Đường thẳng \(y = 3\) cắt hai đồ thị tại các điểm có hoành độ \({x_1},\,\,{x_2}.\) Biết rằng \({x_2} = 2{x_1},\) giá trị của \(\dfrac{a}{b}\) bằng:
Cho $a > 0;a \ne 1,b > 0$, khi đó nếu ${\log _a}b = N$ thì:
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
Rút gọn biểu thức $B = \dfrac{{{a^{2\sqrt 2 }} - {b^{2\sqrt 3 }}}}{{{{\left( {{a^{\sqrt 2 }} - {b^{\sqrt 3 }}} \right)}^2}}} + 1$ ta được kết quả là:
Đồ thị hàm số $y = {x^3} - \left( {3m + 1} \right){x^2} + \left( {{m^2} + 3m + 2} \right)x + 3$ có điểm cực tiểu và điểm cực đại nằm về hai phía của trục tung khi:
Hai hình tứ diện có các cạnh tương ứng bằng nhau thì chúng:
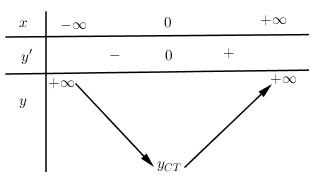
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
Cho tứ diện \(ABCD\) có \(G\) là điểm thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Mặt phẳng thay đổi chứa \(BG\) và cắt \(AC,\,\,AD\) lần lượt tại \(M\) và \(N\). Giá trị nhỏ nhất của tỉ số \(\dfrac{{{V_{ABMN}}}}{{{V_{ABCD}}}}\) là