Đề thi giữa HK2 môn Toán 7 năm 2021 - Trường THCS Kiên Thành
-
Hocon247
-
40 câu hỏi
-
60 phút
-
53 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Viết biểu thức biểu diễn tích 4 số nguyên liên tiếp.
4 số nguyên liên tiếp có dạng \(n;(n+1);(n+2);(n+3)\) với \(n\in\mathbb{Z}\)
Khi đó tích 4 số nguyên liên tiếp là \(n(n+1)(n+2)(n+3)\)
Viết biểu thức biểu diễn tổng các bình phương 2 số lẻ liên tiếp.
2 số lẻ liên tiếp có dạng 2n+1 và 2n+3
bình phương của hai số lẻ lần lượt là \((2 n+1)^{2};(2 n+3)^{2}\)
Vậy tổng các bình phương 2 số lẻ liên tiếp là \((2 n+1)^{2}+(2 n+3)^{2}\)
Viết biểu thức biểu diễn tổng các bình phương 2 số lẻ liên tiếp.
2 số lẻ liên tiếp có dạng 2n+1 và 2n+3
bình phương của hai số lẻ lần lượt là \((2 n+1)^{2};(2 n+3)^{2}\)
Vậy tổng các bình phương 2 số lẻ liên tiếp là \((2 n+1)^{2}+(2 n+3)^{2}\)
Viết biểu thức tính diện tích hình thang có hai đáy a,b chiều cao h?
Diện tích hình thang= \((a+b) \cdot h: 2\)
Tích của tổng hai số x và 4 với hiệu hai số x và 4 là:
Tổng hai số x và 4: x+4
Hiệu hai số x và 4: x-4
Vậy tích của tổng hai số x và 4 với hiệu hai số x và 4 là:\((x+4)(x-4)\)
Bình phương của tổng 3 số a,b,c là:
Tổng ba số a, b, c là a+b+c
Vậy bình phương của tổng 3 số a,b,c là:\((a+b+c)^{2}\)
Thời gian làm bài tập của các học sinh lớp 7 tính bằng phút đước thống kê bởi bảng sau:
Số các giá trị là bao nhiêu?
Số các giá trị là số các đơn vị điểu tra. Số các giá trị là 40
Thời gian bơi ếch 50 m (tính theo giây) của 30 học sinh nữ được ghi trong bảng sau:
.png)
Dấu hiệu ở đây là gì ? Số các giá trị là bao nhiêu ?
Dấu hiệu: thời gian bơi ếch 50m (tính theo giây) của 30 học sinh nữ. Số các giá trị là 30.
Giá trị của biểu thức \(A=\frac{1}{5} x-3 y \text { tại } x=5 \text { và } y=3\) là?
Thế x=5 và y=3 vào biểu thức A ta có
\(A=\frac{1}{5} \cdot 5-3 \cdot 3=-8\)
Cho \(M(x)=4 x^{3}+2 x^{4}-x^{2}-x^{3}+2 x^{2}-x^{4}+1-3 x^{3}\) . Tính \(M(-1)\)
Ta có
\(M(x)=\left(2 x^{4}-x^{4}\right)+\left(4 x^{3}-x^{3}-3 x^{3}\right)+\left(-x^{2}+2 x^{2}\right)+1=x^{4}-x^{2}+1\)
Khi đó
\(M(-1)=(-1)^{4}-(-1)^{2}+1=1\)
Cho đa thức \(f(x, y)=2 y-x-\{2 x-y-[y+3 x-(5 y-x)]\}\). Tính giá trị của đa thức với \(x=a^{2}+2 a b+b^{2}, y=a^{2}-2 a b+b^{2}\) ta được
Ta có
\(f(x, y)=2 y-x-2 x+y+[y+3 x-(5 y-x)]=3 y-3 x+y+3 x-5 y+x=x-y\)
Thay \(x=a^{2}+2 a b+b^{2}, y=a^{2}-2 a b+b^{2}\) vào f(x;y) ta được
\(f(x, y)=a^{2}+2 a b+b^{2}-\left(a^{2}-2 a b+b^{2}\right)=a^{2}+2 a b+b^{2}-a^{2}+2 a b-b^{2}=4 a b\)
Cho \(f(x)=x^{8}-101 x^{7}+101 x^{6}-101 x^{5}+\cdots+101 x^{2}-101 x+25 . \operatorname{Tính} f(100)\)
Ta có \(f(x)=x^{7}(x-100)+x^{5}(x-100)+x^{3}(x-100)+x(x-100)-x^{7}-x^{5}-x^{3}-x+25\)
Thay \(x=100 \text { vào } f(x)\) ta được
\(f(x)=-100^{7}-100^{5}-100^{3}-100+25=-100010001000100+25=-100010001000075\)
Biểu thức \((x+7)^{2}+5\) đạt giá trị nhỏ nhất khi?
Vì \((x+7)^{2} \geq 0 \text { nên }(x+7)^{2}+5 \geq 0+5\)
Suy ra \((x+7)^{2}+5\) nhỏ nhất bằng 5 khi \(x+7=0 \text { suy ra } x=-7\)
Giá trị của biểu thức đại số \(B=2(x-y)+y^{2} \text { tại } x=2, y=-1\)
Thay x=2, y=-1 vào B ta có
\(B=2(2+1)+(-1)^{2}=7\)
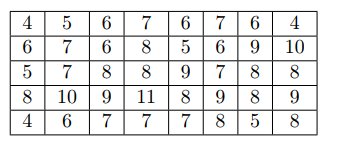
Thời gian làm bài tập của các học sinh lớp 7 tính bằng phút đước thống kê bởi bảng sau:
.png)
Số các giá trị khác nhau là?
Các giá trị khác nhau là: 4,5,6,7,8,9,10,11.
Vậy có 8 giá trị khác nhau.
Điểm kiểm tra môn Tiếng Anh của lớp 7C được cho trong bảng tần số sau:
.png)
Dấu hiệu ở đây là gì ? Số các giá trị là bao nhiêu ?
Dấu hiệu: điểm kiểm tra môn Tiếng Anh của lớp 7C. Số các giá trị là 8
Cho \(A=-12 x y z ; B=\left(-\frac{4}{3} x^{2} y^{3} z\right) \cdot y\). Xác định A.(-B)
Ta có \(A(- B)=-12 x y z \cdot\left(\frac{4}{3} x^{2} y^{3} z\right) \cdot y=-16 x^{3} y^{5} z^{2}\)
Cho \(A=5 a x^{2} y z ; B=\left(-8 x y^{3} b z\right)^{2}(a, b \text { hằng số })\). Xác định phần biến của A.B
Ta có \(A B=5 a x^{2} y z \cdot\left(-8 x y^{3} b z\right)^{2}=5 a x^{2} y z .64 x^{2} y^{6} b^{2} z^{2}=320 a b^{2} x^{4} y^{7} z^{3}(a, b \text { hằng số })\)
Phần biến \(x^{4} y^{7} z^{3}\)
Cho \(A=5 a x^{2} y z ; B=\left(-8 x y^{3} b z\right)^{2}(a, b \text { hằng số })\). Tính A.B
Ta có
\(A B=5 a x^{2} y z \cdot\left(-8 x y^{3} b z\right)^{2}=5 a x^{2} y z .64 x^{2} y^{6} b^{2} z^{2}=320 a b^{2} x^{4} y^{7} z^{3}(a, b \text { hằng số })\)
Cho \(A=15 x y^{2} z ; B=\left(-\frac{4}{3} x^{2} y z^{3}\right) ; C=2 x y\). Xác định hệ số của A.B. (-C)
Ta có \(A.B.\left( { - C} \right) = 15x{y^2}z \cdot \left( { - \frac{4}{3}{x^2}y{z^3}} \right).\left( { - 2xy} \right) = 15.\left( { - \frac{4}{3}} \right).\left( { - 2} \right).x.{x^2}.x.{y^2}.y.y.z.{z^3} = 40{x^4}{y^4}{z^4}\)
Hệ số là 40
Cho \(A=15 x y^{2} z ; B=\left(-\frac{4}{3} x^{2} y z^{3}\right) ; C=2 x y\). Tính A.B.C
Ta có \(A. B .C=15 x y^{2} z \cdot\left(-\frac{4}{3} x^{2} y z^{3}\right) \cdot 2 x y=-40 x^{4} y^{4} z^{4}\)
Cho \(A=2 x^{2} y z ; B=-3 x y^{3} z\). Xác dịnh phần biến của -A.B
Ta có \(-A. B=-2 x^{2} y z \cdot(-3) x y^{3} z=6 x^{3} y^{4} z^{2}\)
Phần biến \(x^{3} y^{4} z^{2}\)
Cho các đơn thức \(2 x^{2} y^{3} ; 5 y^{2} x^{3} ;-\frac{1}{2} x^{3} y^{2} ;-\frac{1}{2} x^{2} y^{3}\). Chọn khẳng định đúng
Theo định nghĩa đơn thức đồng dạng ta có \(2 x^{2} y^{3}, 5 x^{2} y^{3},-\frac{1}{2} x^{2} y^{3}\) là các đơn thức đồng dạng.
Thực hiện phép tính \(-3 x^2{y}+\frac{3}{4} x^{2} y\) ta được
Ta có \( - 3{x^2}y + \frac{3}{4}{x^2}y = \left( { - 3 + \frac{3}{4}} \right){x^2}y = - \frac{9}{4}{x^2}y\)
Thực hiện phép tính \(6 x y+3 x y-\frac{1}{5} x y\) ta được
Ta có
\(6xy + 3xy - \frac{1}{5}xy = \left( {6 + 3 - \frac{1}{5}} \right)xy = \frac{{48}}{5}xy\)
Thực hiện phép tính \(2 x y^{2} z-5 x y^{2} z+\frac{1}{2} x y^{2} z\) ta được
\(2x{y^2}z - 5x{y^2}z + \frac{1}{2}x{y^2}z = \left( {2 - 5 + \frac{1}{2}} \right)x{y^2}z = - \frac{5}{2}x{y^2}z\)
Các đơn thức đồng dạng trong các đơn thức sau là: \(2 x y^{2} z, 6 x y,-3 x^{2} y,-5 x y^{2} z, 3 x y, \frac{3}{4} x^{2} y, \frac{1}{2} x y^{2} z,-\frac{1}{5} x y\)
Các đơn thức đồng dạng là các đơn thức có chung phần biến nên \(6 x y;3 x y;\frac{1}{5} x y\) là các đơn thức đồng dạng.
Các đơn thức đồng dạng trong các đơn thức sau là: \(2 x y^{2} z, 6 x y,-3 x^{2} y,-5 x y^{2} z, 3 x y, \frac{3}{4} x^{2} y, \frac{1}{2} x y^{2} z,-\frac{1}{5} x y\)
Đơn thức đồng dạng là đơn thức có chung phần biến.
Các đơn thức \(2 x y^{2} z;5 x y^{2} z;\frac{1}{2} x y^{2} z\) có phần biến là \(x y^{2} z\) nên chúng đồng dạng.
Cho tam giác ABC có AB < AC. Trên đường phân giác AD lấy điểm E. Chọn câu đúng.
Trên cạnh AC lấy điểm K sao cho: AK=AB
Xét ΔABE và ΔAKE có:
AB=AK (cách dựng)
\(\widehat {BAE} = \widehat {KAE}\) vì AD là tia phân giác \(\widehat {BAC}\))
AE cạnh chung
⇒ΔABE=ΔAKE(c.g.c)
⇒EB=EK(hai cạnh tương ứng).
Áp dụng bất đẳng thức tam giác vào ΔCEK ta có: EC−EK
suy ra EC−EB
Mặt khác: KC=AC−AK=AC−AB (vì AK=AB theo cách dựng) (2)
Từ (1) và (2) suy ra:EC−EB
Cho tam giác ABC có M là trung điểm BC. So sánh AB + AC và 2AM.
Trên tia đối của tia MA lấy điểm N sao cho MN=MA
Vì M là trung điểm của BC ⇒ MB=MC (tính chất trung điểm)
Xét ΔMAB và ΔMNC có:
\(\begin{array}{l} MB = MC\left( {cmt} \right)\\ \widehat {AMB} = \widehat {NMC}(dd)\\ AM = MN(gt) \end{array}\)
\(⇒ΔMAB=ΔMNC(c−g−c)⇒NC=AB(1)\) (2 cạnh tương ứng)
Xét ΔACN có: AN
Từ(1)(2) ⇒ AN < AC + AB
Mặt khác: AN = 2AM (gt) => 2AM < AB + AC
Cho tam giác ABC cân tại A có một cạnh bằng 5cm. Tính cạnh BC của tam giác đó biết chu vi của tam giác là 17cm.
Giả sử ΔABC cân tại A.
- Trường hợp 1:
\(AB=AC=5cm⇒BC=17−5−5=7cm\)
Ta có: \(\left\{ \begin{array}{l} AB + AC = 5 + 5 = 10 > BC = 7\\ AB + BC = 5 + 7 = 12 > AC = 5\\ BC + AC = 7 + 5=12 > AB = 5 \end{array} \right.\) (thỏa mãn bất đẳng thức tam giác)
- Trường hợp 2:
\( BC = 5cm \Rightarrow AB = AC = \left( {17 - 5} \right):2 = 6cm\)
Ta có: \(\left\{ \begin{array}{l} AB + AC = 6 + 6 = 12 > BC = 5\\ AB + BC = 5 + 6 = 11 > AC = 6\\ BC + AC = 6 + 5 = 11 > AB = 6 \end{array} \right.\) (thỏa mãn bất đẳng thức tam giác)
Vậy nếu ΔABC cân tại A có
\(\left[ \begin{array}{l} AB = AC = 5cm \to BC = 7cm\\ BC = 5cm \to AB = AC = 6cm \end{array} \right.\)
Vậy: BC=7cm hoặc BC=5cm.
Cho tam giác ABC có BC = 5cm, AC = 1cm và độ dài cạnh AB là một số nguyên. Tam giác ABC là tam giác gì?
Gọi độ dài cạnh AB là x(x>0)
Theo bất đẳng thức tam giác ta có:
5−1
Vì x là số nguyên nên x=5. Độ dài cạnh AB=5cm
Tam giác ABC có: AB=BC=5cm nên tam giác ABC cân tại B.
Cho tam giác ABC có BC = 1cm, AC = 8cm và độ dài cạnh AB là một số nguyên (cm). Tam giác ABC là tam giác gì?
Gọi độ dài cạnh AB là x(x>0)
Theo bất đẳng thức tam giác ta có:
8−1
Vì x là số nguyên nên x=8. Độ dài cạnh AB=8cm
Tam giác ABC có AB=AC=8cm nên tam giác ABC cân tại A.
Cho tam giác ABC biết AB = 2cm; BC = 7cm và cạnh AC là một số tự nhiên lẻ. Chu vi tam giác ABC là:
Gọi độ dài cạnh AC là x(x>0)
Theo bất đẳng thức tam giác ta có:
7−2
Vì x là số tự nhiên lẻ nên x=7. Độ dài cạnh AC=7cm.
Chu vi tam giác ABC là:
AB+BC+AC=2+7+7=16(cm)
Cho tam giác ABC có AB = 16 cm; AC = 25 cm. Vẽ đường trung trực của BC cắt AC tại D. Chu vi tam giác ABD là:
.png)
D thuộc đường trung trực của đoạn thẳng BC nên DB = DC (tính chất điểm thuộc đường trung trực của đoạn thẳng)
Chu vi tam giác ABD là:
AB + DB + AD = AB + DC + AD = AB + (CD + AD) = AB + AC = 16 + 25 = 41 cm
Vậy chu vi tam giác ABC là 41 cm.
Chọn đáp án B
Cho đoạn thẳng AB. Gọi O là trung điểm của AB. Trong hai nửa mặt phẳng bờ là đường thẳng AB lấy hai điểm M và N sao cho MA = MB và NA = NB.
.png)
Ta có: MA = MB nên M thuộc đường trung trực của đoạn thẳng AB
Tương tự NA = NB nên N thuộc đường trung trực của đoạn thẳng AB
Suy ra MN là đường trung trực của đoạn thẳng AB
Mà O là trung điểm của AB
Vậy MN vuông góc với AB tại O.
Chọn đáp án C
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
.png)
Giả sử ΔABC có AM là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh ΔABC là tam giác cân. Thật vậy, vì AM là trung tuyến của ΔABC (gt) ⇒ BM = MC (tính chất trung tuyến)
Vì AM là trung trực của BC ⇒ AM ⊥ BC
Xét hai tam giác vuông ΔABM và ΔACM có:
BM = CM (cmt)
AM chung
Do đó ΔABM = ΔACM (2 cạnh góc vuông)
⇒ AB = AC (2 cạnh tương ứng) ⇒ ΔABC cân tại A
Chọn đáp án B
Cho điểm C thuộc trung trực của đoạn thẳng AB. Biết CA = 10 cm. Độ dài đoạn thẳng CB là:
Vì C thuộc đường trung trực của đoạn thẳng AB nên CA = CB (tính chất điểm thuộc đường trung trực của đoạn thẳng)
Mà CA = 10 cm
Do đó CB = 10 cm.
Chọn đáp án A
Em hãy chọn câu đúng nhất
+ Trọng tâm là giao điểm của ba đường trung tuyến nên đáp án A sai. Loại đáp án A
+ Giao điểm ba đường phân giác của tam giác cách đều ba cạnh của tam giác là đúng.
+ Trong một tam giác, đường trung tuyến xuất phát từ một đỉnh đồng thời là đường phân giác ứng với cạnh đáy khi tam giác đó là tam giác cân tại đỉnh ấy nên C sai
+ Giao điểm ba đường phân giác của tam giác là tâm đường tròn ngoại tiếp tam giác đó là sai vì giao điểm ba đường phân giác của tam giác là tâm đường tròn nội tiếp tam giác đó
Chọn đáp án B
Cho tam giác ABC có hai đường phân giác CD và BE cắt nhau tại I. Khi đó
Hai đường phân giác CD và DE cắt nhau tại I mà ba đường phân giác của tam giác cùng đi qua một điểm nên AI là phân giác góc A
Chọn đáp án D

.PNG)
