Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Võ Văn Kiệt
Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Võ Văn Kiệt
-
Hocon247
-
50 câu hỏi
-
60 phút
-
94 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hàm số \(y=x^{4}-4 x^{3}+3\) đồng biến trên những khoảng nào sau đây?
Ta có \(y^{\prime}=4 x^{3}-12 x^{2}=4 x^{2}(x-3)>0 \Leftrightarrow x>3\)
Vậy hàm số đồng biến trên \((3 ;+\infty)\)
Hàm số f (x) đồng biến trên khoảng \((0 ;+\infty)\), khẳng định nào sau đây đúng ?
Ta có hàm số f (x) đồng biến trên (a; b).
\(\begin{aligned} &\text { Do đó với mọi } x_{1}, x_{2} \in(a ; b) \text { và } x_{1}<x_{2} \text { suy ra } f\left(x_{1}\right)<f\left(x_{2}\right)\\ &\operatorname{Nên} f\left(\frac{4}{3}\right)>f\left(\frac{5}{4}\right) \end{aligned}\)
Hàm số \(y=x^{3}-3 x^{2}-9 x+1\) đồng biến trên khoảng nào trong những khoảng sau?
\(\begin{aligned} &\text { TXĐ: } D=\mathbb{R} . \text { Đạo hàm: } y^{\prime}=3 x^{2}-6 x-9 \text { . }\\ &\text { Xét } y^{\prime}=0 \Rightarrow 3 x^{2}-6 x-9=0 \Leftrightarrow\left[\begin{array}{l} x=3 \Rightarrow y=-26 \\ x=-1 \Rightarrow y=6 \end{array} .\right. \end{aligned}\)
Bảng biến thiên:
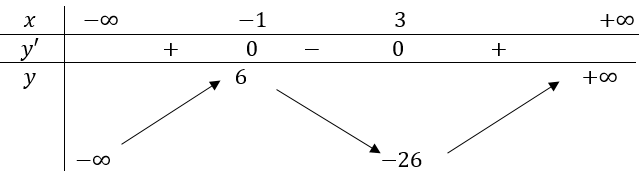
Hàm số đồng biến trên các khoảng \((-\infty ;-1) \text { và }(3 ;+\infty)\)
Chọn B
Cho hàm số f (x) có đạo hàm trên và \(f^{\prime}(x)>0, \forall x>0 . \text { Biết } f(1)=2\) , hỏi khẳng định nào sau đây có thể xảy ra?
\(\begin{aligned} &\text { Vì } f^{\prime}(x)>0, \forall x>0 \text { nên hàm số } f(x) \text { đồng biến trên }(0,+\infty) \text { . }\\ &\text { Do đó: }\left\{\begin{array}{l} f(2)>f(1)=2 \\ f(3)>f(1)=2 \end{array} \Rightarrow f(2)+f(3)>4\right.\\ &f(2017)>f(2016) \end{aligned}\)
Vậy D có thể xảy ra
Hàm số nào sau đây luôn nghịch biến trên \(\mathbb{R}\)?
Hàm phân thức không thể đồng biến trên \(\mathbb{R}\) nên loại B và C.
Xét hàm số \(y=-x^{3}-2 x+3 \text { có } \operatorname{TXD} D=\mathbb{R}, y^{\prime}=-3 x^{2}-2<0 \forall x \in \mathbb{R}\) nên nghịch biến trên \(\mathbb{R}\)
Hàm số \(y=f(x)=\frac{-2}{-x+1}\) có tính chất?
Ta có \(y^{\prime}=f^{\prime}(x)=\frac{-2}{(-x+1)^{2}}<0 \quad \forall x \neq 1\)
Suy ra hàm số nghịch biến trên từng khoảng xác định
Hàm số \(y=x^{3}-x^{2}-x+3\) nghịch biến trên khoảng
\(y=x^{3}-x^{2}-x+3 \Rightarrow y^{\prime}=3 x^{2}-2 x-1 . y^{\prime}=0 \Leftrightarrow x=1 \text { hoặc } x=-\frac{1}{3}\)
Bẳng biến thiên:
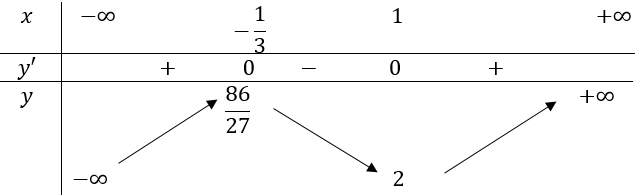
Vậy hàm số nghịch biến trên \(\left(-\frac{1}{3} ; 1\right)\)
Cho hàm số \(y=x^{3}-2 x^{2}+x+1\). Mệnh đề nào dưới đây đúng ?
Ta có
\(y^{\prime}=3 x^{2}-4 x+1 \Rightarrow y^{\prime}=0 \Leftrightarrow x=1 \text { hoặc } x=\frac{1}{3}\)
Bẳng biến thiên:
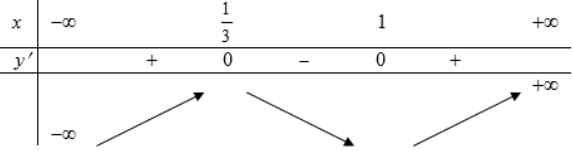 Vậy hàm số nghịch biến trên \(\left(\frac{1}{3} ; 1\right)\)
Vậy hàm số nghịch biến trên \(\left(\frac{1}{3} ; 1\right)\)
Hàm số nào sau đây đồng biến trên \(\mathbb{R} ?\)
Chọn vì xét hàm số \(y=x^{3}-3 x^{2}+3 x+5\) ta có
\(y^{\prime}=3 x^{2}-6 x+3 \geq 0, \forall x \in \mathbb{R}\) và \(y^{\prime}=0 \Leftrightarrow 3 x^{2}-6 x+3=0 \Leftrightarrow x=1\)
Nên hàm số \(y=x^{3}-3 x^{2}+3 x+5\) đồng biến trên \(\mathbb{R} \)
Bảng biến thiên trong hình vẽ là của hàm số nào sau đây?
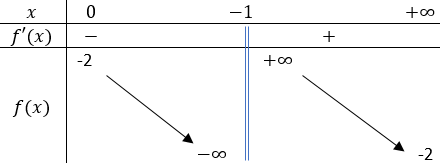
Theo bảng biến thiên thì đồ thị hàm số có tiệm cận ngang y=-2 nên loại A, D.
Lại có y'< 0 , \(\forall x \neq-2\) nên loại B
Bảng biến thiên sau đây là của hàm số
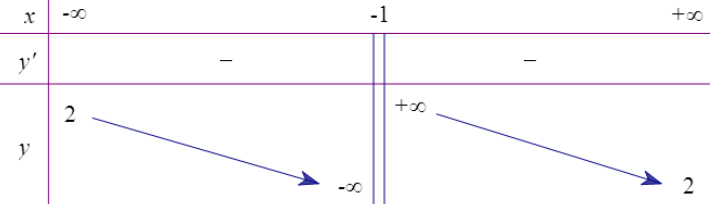
Dựa vào bảng biển thiên ta có
\(\begin{aligned} &\mathrm{TCD}: x=-1 \Leftrightarrow x+1=0\\ &\text { TCN: }y=2\\ &y^{\prime}<0 \text { với mọi } x \neq-1 \end{aligned}\)
nên chọn D
Cho bảng biến thiên như hình vẽ bên. Hỏi đây là bảng biến thiên của hàm số nào trong các hàm số sau?
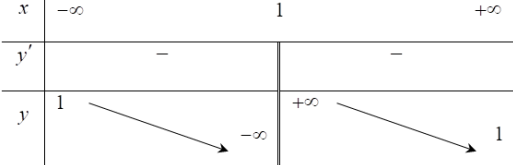
Từ bảng biến thiên ta có đồ thị hàm số có đường tiệm cận đứng là x =1 và đường tiệm cận ngang là y =1 nên ta loại các đáp án B và D.
Mặt khác từ bảng biến thiên ta có hàm số nghịch biến nên lọai đáp án C
Cho hàm số y=f(x) có bảng biến thiên như sau:
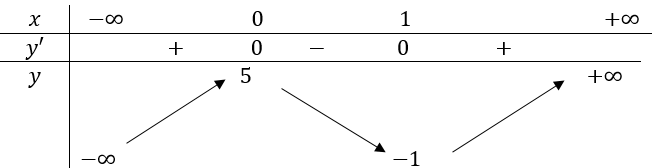
Hàm số đồng biến trên khoảng nào dưới đây?
trên khoảng \((-\infty ; 0)\) thì y'>0 nên hàm số đồng biến.
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
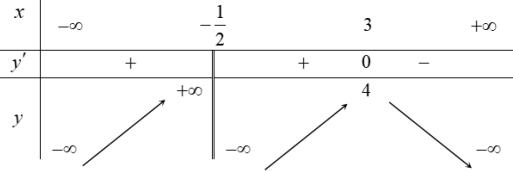
Dựa vào bảng biến thiên nhận thấy trên khoảng \((3 ;+\infty)\) thì y'<0 nên hàm số nghịch biến trên \((3 ;+\infty)\)
Cho hàm số \(y=x^{3}-3 x^{2}+2\) . Khẳng định nào sau đây là đúng?
\(y^{\prime}=3 x^{2}-6 x=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=2 \end{array}\right.\)
Lập bảng biến thiên ta được hàm số đạt cực đại tại x = 2 và đạt cực tiểu tại x = 0
Cho hàm số \(y=x^{4}-2 x^{2}+3\) . Khẳng định nào sau đây là đúng?
\(y^{\prime}=4 x^{3}-4 x=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=1 \\ x=-1 \end{array}\right.\)
Vậy hàm số có ba cực trị.
Biết đồ thị hàm số \(y=x^{3}-3 x+1\) có hai điểm cực trị A, B. Khi đó phương trình đường thẳng AB là
\(\begin{array}{l} y^{\prime}=3 x^{2}-3=0 \Leftrightarrow\left[\begin{array}{l} x=1 \\ x=-1 \end{array}\right. \\ \Rightarrow A(1 ;-1), \mathrm{B}(-1 ; 3) \Rightarrow \text { Phương trình } A B: y=-2 x+1 \end{array}\)
Cho hàm số y=f(x) có đồ thị như hình vẽ:
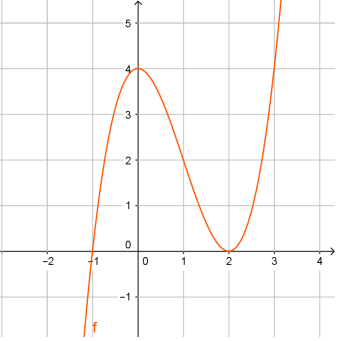
Đồ thị hàm số y=f(x) có mấy điểm cực trị?
Dựa vào đồ thị hàm số nhận thấy khi đi qua x=0 và x=2 thì đồ thị hàm số đổi chiều chuyển động nên đồ thị hàm số có hai điểm cực trị.
Cho hàm số y=f(x) có bảng biến thiên:
.png)
Khẳng định nào sau đây là đúng?
Nhận thấy khi đi qua điểm x=2 thì hàm số dổi dấu từ dương sang âm nên x=2 là cực đại của hàm số.
Khi đi qua điểm x=4 thì hàm số dổi dấu từ âm sang dương nên x=4 là cực tiểu của hàm số.
Gọi M n , lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số \(y=\frac{x^{2}+3 x+3}{x+2}\). Khi đó giá trị của biểu thức \(M^{2}-2 n\) bằng:
\(\begin{array}{l} y^{\prime}=\frac{x^{2}+4 x+3}{(x+2)^{2}} \\ y^{\prime}=0 \Leftrightarrow \frac{x^{2}+4 x+3}{(x+2)^{2}}=0 \Leftrightarrow\left[\begin{array}{l} x=-3 \\ x=-1 \end{array}\right. \end{array}\)
Hàm số đạt cực đại tại \(x=-3 \text { và } y_{C Đ}=-3\)
Hàm số đạt cực tiểu tại \(x=-1 \text { và } y_{C T}=1\)
\(\Rightarrow M^{2}-2 n=7\)
Tìm tất cả các giá trị của tham số m để hàm số \(y=x^{3}-m x^{2}+(2 m-3) x-3\) đạt cực đại tại x =1.
Để hàm số đạt cực đại x =1 thì \(\left\{\begin{array}{l} y^{\prime}(1)=3.1^{2}-2 m \cdot 1+2 m-3=0 \\ y^{\prime \prime}(1)=6 \cdot 1-2 m<0 \end{array} \Leftrightarrow m>3\right.\)
Hàm số \(y=x^{4}+2(m-2) x^{2}+m^{2}-2 m+3\) có đúng 1 điểm cực trị thì giá trị của m là:
Hàm trùng phương có 1 điểm cực trị khi \(a b \geq 0 \Leftrightarrow m-2 \geq 0 \Leftrightarrow m \geq 2 \text { . }\)
Cho hàm số \(f(x)=\frac{a x+b}{c x+d}(a, b, c, d \in \mathbb{R}, a>0)\)có bảng biến thiên như sau:
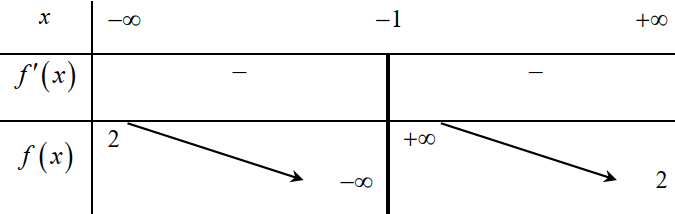
Trong các mệnh đề dưới đây, mệnh đề nào đúng?
Hàm số có tiệm cận ngang \(y=2>0 \Rightarrow \frac{a}{c}>0, \text { mà } a>0 \Rightarrow c>0\)
Hàm số có tiệm cận đứng \(x=-1<0 \Rightarrow-\frac{d}{c}<0 \Rightarrow \frac{d}{c}>0, \text { mà } c>0 \Rightarrow d>0\)
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ \(x<-1<0\)
\(\Rightarrow-\frac{b}{a}<0 \Rightarrow \frac{b}{a}>0 \Rightarrow b>0\)
Cho hàm số \(y=a x^{4}+b x^{2}+c \quad a \neq 0\) có bảng biến thiên dưới đây:
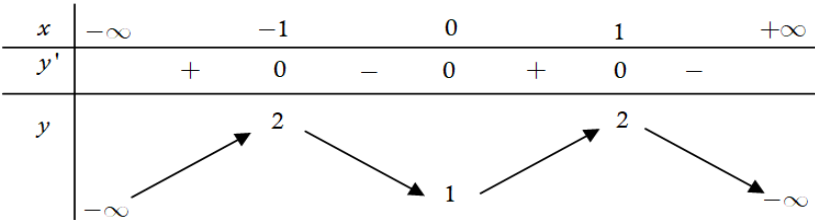
Tính \(P=a-2 b+3 c\)
Ta có \(y^{\prime}=4 a x^{3}+2 b x=2 x\left(2 a x^{2}+b\right), y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x^{2}=-\frac{b}{2 a} \end{array}\right.\)
Căn cứ vào bảng biến thiên ta thấy a < 0 ; b > 0 , hàm đạt cực đại tại \(x=\pm 1 \text { và } y(\pm 1)=2\) , hàm đạt cực tiểu tại x = 0 và y ( 0) =1 .
Suy ra, \(\left\{\begin{array}{l} -\frac{b}{2 a}=1 \\ a+b+c=2 \\ c=1 \end{array}\right.\)\(\Leftrightarrow\left\{\begin{array}{l} a=-1 \\ b=2 \\ c=1 \end{array}\right.\)
Do đó \(P=a-2 b+3 c=-2\)
Cho hàm số y =f(x) có bảng xét dấu đạo hàm như sau:

Mệnh đề nào sau đây đúng
Dựa vào bảng xét dấu của đạo hàm ta có trong khoảng \((0 ;+\infty)\) hàm số có duy nhất một điểm cực trị và điểm đó là điểm cực đại của đồ thị hàm số. Vậy trong khoảng \((0 ;+\infty)\) hàm số đạt giá trị lớn nhất tại \(x=1 \text { hay } \max\limits _{(0 ;+\infty)} f(x)=f(1)\)
Tìm giá trị nhỏ nhất m của hàm số \(y=x^{3}-3 x^{2}-9 x+5\) trên đoạn [-2;2].
\(\begin{aligned} &\text { Xét hàm số } y=x^{3}-3 x^{2}-9 x+5 \text { trên đoạn }[-2 ; 2]\\ &y^{\prime}=3 x^{2}-6 x-9\\ &y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} x=-1 \in[-2 ; 2] \\ x=3 \quad \notin[-2 ; 2] \end{array}\right.\\ & y(-2)=3 ; y(2)=-17 ; y(-1)=10\\ &\text { Vậy } m=\min _{[-2 ; 2]} y=-17 \text { . } \end{aligned}\)
Cho hàm số y =f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên.
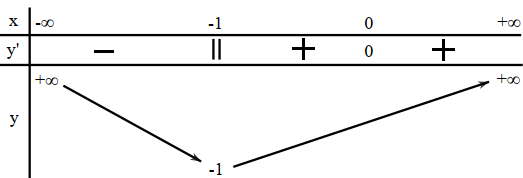
Khẳng định nào sau đây là khẳng định đúng?
Nhìn BBT ta thấy y =-1 là giá trị nhỏ nhất của hàm số
Cho hàm số y \(y=f(x)\) xác định và liên tục trên khoảng \(\left(-\infty ; \frac{1}{2}\right) \text { và }\left(\frac{1}{2} ;+\infty\right)\) . Đồ thị hàm số \(y=f(x)\) là đường cong trong hình vẽ bên
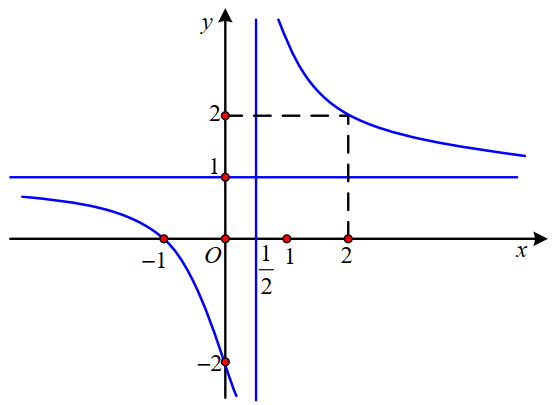
Tìm mệnh đề đúng trong các mệnh đề sau:
Chọn D vì
Trên đoạn [-3 ; 0] hàm số liên tục và \(f(-3)>f(0)\) nên \(\max\limits _{[-3 ; 0]} f(x)=f(-3)\)
Trên khoảng \((0 ;+\infty)\) thì hàm số \(y=-x^{3}+3 x+1\)
\(y^{\prime}=-3 x^{2}+3 . \text { Cho } y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} x=1 \\ x=-1 \end{array}\right.\)
Bảng biến thiên của hàm số trên \((0 ;+\infty)\)
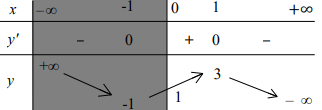
Vây chọn D: Hàm số có giá trị lớn nhất là 3
Giá trị nhỏ nhất của hàm số \(f(x)=\frac{x^{2}+x+4}{x+1}\) trên đoạn [0;2] bằng
Hàm số luôn xác định trên [0;2].
Mặt khác
\(f^{\prime}(x)=\frac{x^{2}+2 x-3}{(x+1)^{2}} ; f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=-3 \notin[0 ; 2] \\ x=1 \in[0 ; 2] \end{array}\right.\)
Ta có \(f(0)=4 ; f(1)=3 ; f(2)=\frac{10}{3}\)
Vậy \(\min\limits _{[0 ; 2]} f(x)=f(1)=3\)
Tìm các giá trị của tham số m để bất phương trình \(\frac{x^{2}+3 x+3}{x+1} \geq m\) nghiệm đúng với mọi \(x \in[0 ; 1]\)
\(\begin{aligned} &\text { Đặt } f(x)=\frac{x^{2}+3 x+3}{x+1} . \text { Bất phương trình } \frac{x^{2}+3 x+3}{x+1} \geq m \text { nghiệm đúng với mọi } x \in[0 ; 1] \text { khi và }\\ &\text { chỉ khi } m \leq \min _{[0 ; 1]} f(x)\\ &\text { Ta có } f^{\prime}(x)=\frac{x^{2}+2 x}{(x+1)^{2}} \geq 0 \text { với mọi } x \in[0 ; 1] \Rightarrow f(x) \text { đồng biến trên }[0 ; 1]\\ &\Rightarrow \min _{[0 ; 1]} f(x)=f(0)=3 . \text { Vậy } m \leq 3 \end{aligned}\)
Cho hàm số \(y=\frac{x\left(\sqrt{x^{2}+3}-2\right)}{x^{2}+2 x+1}\) có đồ thị (C). Khẳng định nào sau đây là đúng ?
TXĐ: \(D=\mathbb{R} \backslash\{-1\}\)
Ta có
\(\begin{array}{l} \lim\limits _{x \rightarrow-1^{+}} \frac{x\left(\sqrt{x^{2}+3}-2\right)}{x^{2}+2 x+1}=\lim\limits _{x \rightarrow-1^{+}} \frac{x\left(x^{2}-1\right)}{\left(x^{2}+2 x+1\right)\left(\sqrt{x^{2}+3}+2\right)}= \lim\limits _{x \rightarrow-1^{+}} \frac{x(x-1)}{(x+1)\left(\sqrt{x^{2}+3}+2\right)}=+\infty \\ \lim\limits _{x \rightarrow-1^{-}} \frac{x\left(\sqrt{x^{2}+3}-2\right)}{x^{2}+2 x+1}=\lim\limits _{x \rightarrow-1^{-}} \frac{x\left(x^{2}-1\right)}{\left(x^{2}+2 x+1\right)\left(\sqrt{x^{2}+3}+2\right)} =\lim\limits _{x \rightarrow-1^{-}} \frac{x(x-1)}{(x+1)\left(\sqrt{x^{2}+3}+2\right)}=-\infty \end{array}\)
Vậy đồ thị hàm số có tiệm cận đứng là x=1.
Lại có
\(\begin{array}{l} \lim\limits _{x \rightarrow+\infty} \frac{x\left(\sqrt{x^{2}+3}-2\right)}{x^{2}+2 x+1}=\lim\limits _{x \rightarrow+\infty} \frac{x^{2}\left(\sqrt{1+\frac{3}{x^{2}}}-\frac{2}{x}\right)}{x^{2}\left(1+\frac{2}{x}+\frac{1}{x^{2}}\right)}=1 \\ \text{ Vậy đồ thị hàm số có tiệm cận ngang là y=1}\\ \lim\limits _{x \rightarrow-\infty} \frac{x\left(\sqrt{x^{2}+3}-2\right)}{x^{2}+2 x+1}=\lim\limits _{x \rightarrow+\infty} \frac{-x^{2}\left(\sqrt{1+\frac{3}{x^{2}}}-\frac{2}{x}\right)}{x^{2}\left(1+\frac{2}{x}+\frac{1}{x^{2}}\right)}=-1\\ \text{ Vậy đồ thị hàm số có tiệm cận ngang là y=-1} \end{array}\)
Cho hàm số f(x) có đồ thị như hình vẽ bên. Tiệm cận đứng và tiệm cận ngang của đồ thị lầnlượt là
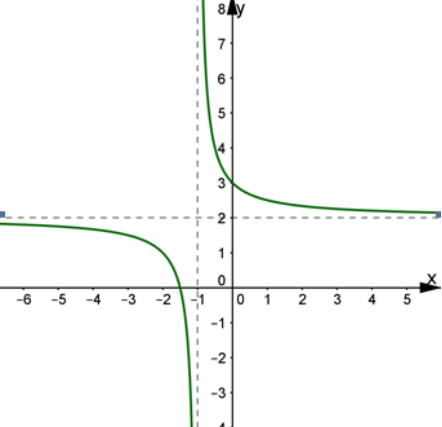
Nhìn vào đồ thị ta suy ra ngay tiệm cận đứng và tiệm cận ngang lần lượt là các đường thẳng \(x=-1 ; y=2\)
Cho hàm số y= f (x) có bảng biên thiên như sau:
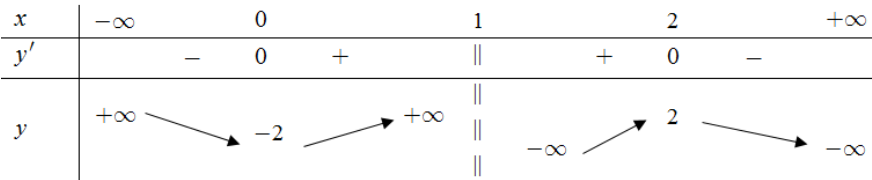
Kết luận nào sau đây là đúng?
A sai vì hàm số đồng biến trên (0;1) và (1;2)
B sai vì \(f_{G T}(x)=-2 ; f_{\mathrm{CD}}(x)=2\)
C sai vì hàm số nghịch biến trên \((-\infty ; 0) \text { và }(2 ;+\infty)\)
Cho hàm số y =f(x) có bảng biến thiên sau. Hỏi đồ thị hàm số đó có mấy tiệm cận.
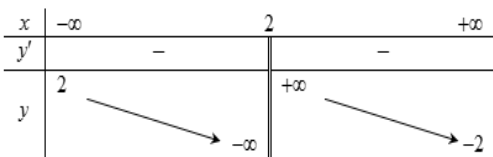
\(\begin{aligned} &\lim _{x \rightarrow-\infty} y=2 \Rightarrow y=2 \text { là tiệm cận ngang. }\\ &\lim _{x \rightarrow+\infty} y=-2 \Rightarrow y=-2 \text { là tiệm cận ngang. }\\ &\lim _{x \rightarrow 2^{-}} y=-\infty, \lim _{x \rightarrow 2^{+}} y=+\infty \Rightarrow x=2 \text { là tiệm cận đứng. } \end{aligned}\)
Vậy đồ thị hàm số có 3 đường tiệm cận.
Số giao điểm của đồ thị hàm số \(y=x^{2} \cdot\left|x^{2}-4\right|\) với đường thẳng y = 3 là
Ta vẽ đồ thị hàm số bằng cách:
+ Vẽ đồ thị hàm số \(y=x^{2} \cdot\left(x^{2}-4\right)\)
+ Lấy đối xứng phần đồ thị nằm trục hoành qua Ox. Bỏ đi phần đồ thị nằm dưới trục hoành, ta được đồ thị sau:
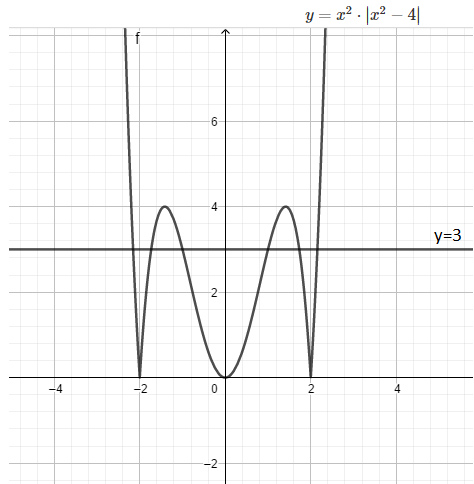
Số giao điểm với đường thẳng y=3 là 6
Đồ thị hàm số \(y=2 x^{3}-x^{2}+x+2\) cắt parabol \(y=-6 x^{2}-4 x-4\) tại một điểm duy nhất. Kí hiệu \(\left(x_{0} ; y_{0}\right)\) là tọa độ điểm đó. Tính giá trị của biểu thức \(x_{0}+y_{0}\)
\(\begin{aligned} &\text { Ta có } x_{0} \text { là nghiệm của phương trình: } 2 x^{3}-x^{2}+x+2=-6 x^{2}-4 x-4\\ &\Leftrightarrow 2 x^{3}+5 x^{2}+5 x+6=0 \Leftrightarrow(x+2)\left(2 x^{2}+x+3\right)=0 \Leftrightarrow x_{0}=-2\\ &\text { Vói } x_{0}=-2 \Rightarrow y_{0}=-20 . \text { Vậy } x_{0}+y_{0}=-22 . \end{aligned}\)
Cho hàm số y =f(x) có bảng biến thiên như hình vẽ sau:
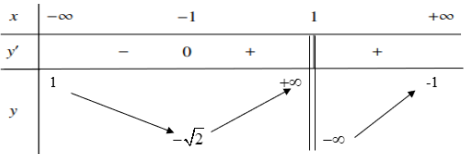
Số nghiệm của phương trình f (x)=-1 là
Số nghiệm của phương trình f(x)=-1 chính là số giao điểm của đồ thị hàm số y =f(x)và đường thẳng y=-1 . Nhìn BBT trên ta thấy đường thẳng y = - 1 cắt đồ thị hàm số y = f(x) tại 2 điểm. Vậy phương trình đã cho có 2 nghiệm
Tìm giá trị lớn nhất của hàm số \(y=\frac{2 x-1}{x+1}\) trên đoạn [1;2].
\(y^{\prime}=\frac{3}{(x+1)^{2}}>0\) nên hàm số đông biến trên các khoảng xác định
Vậy \(\max \limits_{[1 ; 2]} y=f(2)=1\)
Tính tổng giá trị lớn nhất và nhỏ nhất của hàm số \(y=x^{2}+\frac{2}{x}\) trên đoạn \(\left[\frac{1}{2} ; 2\right]\)
\(\begin{aligned} &\text { Hàm số đã cho xác định và liên tục trên }\left[\frac{1}{2} ; 2\right] \text { . }\\ &\text { Ta có }\left\{\begin{array}{l} x \in\left(\frac{1}{2} ; 2\right) \\ y^{\prime}=2 x-\frac{2}{x^{2}}=0 \end{array} \Leftrightarrow x=1\right. \text { . }\\ &\text { Tính được } f\left(\frac{1}{2}\right)=\frac{17}{4} ; f(2)=5 ; f(\mathrm{y})=3\\ &\text { Do đó } \max\limits _{\left[\frac{1}{2} ; 2\right]} y=5 ; \min\limits _{\left[\frac{1}{2} ; 2\right]} y=3 \Rightarrow \max \limits_{\left[\frac{1}{2}, 2\right]} y+\min\limits _{\left[\frac{1}{2}, 2\right]} y=8 \end{aligned}\)
Hình bát diện đều có tất cả bao nhiêu cạnh?
Theo lý thuyết số cạnh của hình bát diện đều là 12 cạnh
Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Biết hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Hình chóp này có bao nhiêu mặt phẳng đối xứng?
Theo giả thiết hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy suy ra \(S A \perp(A B C D)\).
Mặt khác đáy ABCD là hình vuông nên hình chóp S.ABCD chỉ có một mặt phẳng đối xứng là (SAC).
Cho hình chóp tứ giác đều S.ABCD với O là tâm đa giác đáy ABCD . Khẳng định nào sau đây sai?
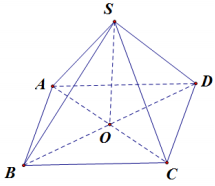
Nếu \(B C \perp(S A B) \Rightarrow B C \perp S B\) nên tam giác SBC vuông tại B . Mà tam giác SBC là tam giác cân tại S : không thể xảy ra.
Một người thợ thủ công làm mô hình đèn lồng bát diện đều, mỗi cạnh của bát diện đó được làm từ các que tre có độ dài 8 cm . Hỏi người đó cần bao nhiêu mét que tre để làm 100 cái đèn (giả sử mối nối giữa các que tre có độ dài không đáng kể)?
Hình bát diện đều là hình có 12 cạnh. Mỗi cạnh có độ dài 8 cm .
Suy ra số mét que tre để làm được một cái đèn hình bát diện đều là: 8.12 =96cm .
Để làm 100 cái đèn như vậy cần số mét tre là: 96.100 =9600 cm = 96 m.
Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy
và SA = 2a . Thể tích khối chóp S.ABCD bằng

\(V_{S . A B C D}=\frac{1}{3} S_{\Delta A B C D} \cdot S A=\frac{1}{3} \cdot a^{2} \cdot 2 a=\frac{2 a^{3}}{3} .\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật \(A B=a, B C=2 a\), cạnh bên SA vuông
góc với đáy và \(S A=a \sqrt{2}\) . Tính thể tích khối chóp S.ABCD.
\(\begin{aligned} &\text { Diện tích đáy: } S_{A B C D}=A B \cdot B C=2 a^{2} \text { . }\\ &\text { Thể tích: } V=\frac{1}{3} S_{A B C D} \cdot S A=\frac{2 a^{3} \sqrt{2}}{3} \end{aligned}\)
Cho tứ diện ABCD có AD vuông góc với mặt phẳng (ABC). Biết đáy ABC là tam giác vuông tại B và AD = 5, AB = 5, BC =12 . Tính thể tích V của tứ diện ABCD .
\(V=\frac{1}{3} A D \cdot \frac{1}{2} A B \cdot B C=\frac{1}{6} .5 .5 .12=50 \)
Cho hình chóp S.ABCD có đáy hình vuông cạnh a ; SA vuông góc mặt đáy; Góc giữa SC và mặt đáy của hình chóp bằng 600 . Thể tích khối chóp S.ABCD là
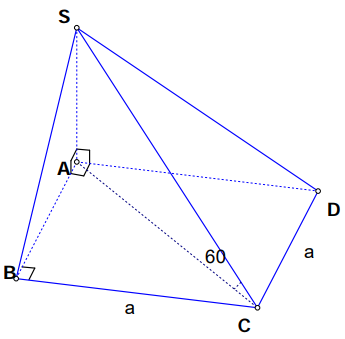
\(\begin{array}{l} \text { Ta có }[S C,(A B C D)]=(S C, A C)=S C A=60^{\circ} \\ S A=A C \cdot \tan 60^{\circ}=a \sqrt{2} \cdot \sqrt{3}=a \sqrt{6} \\ \text { Vậy } V_{A B C D}=\frac{1}{3} S_{A B C D} \cdot S A=\frac{1}{3} a^{2} a \sqrt{6}=\frac{a^{3} \sqrt{6}}{3} \end{array}\)
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B , biết SA=AC=2a . Tính thể tích khối chóp S.ABC .
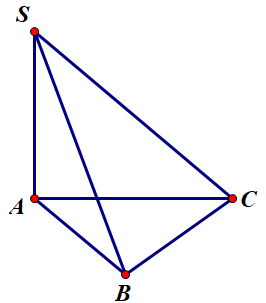
Ta có \(A B=B C=\frac{A C}{\sqrt{2}}=\frac{2 a}{\sqrt{2}}=a \sqrt{2}\)
\(V_{S.ABC}=\frac{1}{3} S_{A B C} \cdot S A=\frac{1}{3} \cdot \frac{1}{2} A B^{2} \cdot S A=\frac{1}{6} \cdot(a \sqrt{2})^{2} \cdot 2 a=\frac{2}{3} a^{3}\)
Cho hình chóp S.BC có đáy ABC là tam giác đều cạnh a . SA vuông góc với đáy và tạo với đường thẳng SB một góc 450. Tính thể tích khối chóp S.ABC.
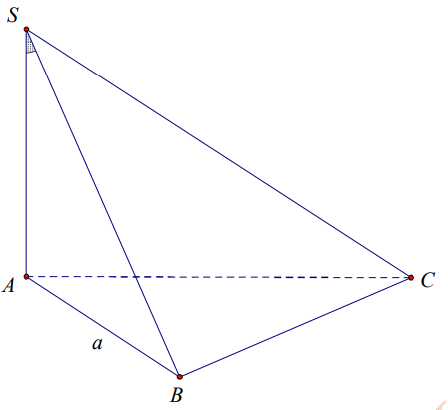
\(\begin{aligned} &\text { Ta có: } S A \perp(A B C) \Rightarrow S A \text { là chiều cao của hình chóp } \Rightarrow S A \perp A B \Rightarrow \Delta S A B \text { vuông tại } A \text { . }\\ &\Rightarrow \widehat{(S A, S B)}=\widehat{A S B}=45^{\circ} \Rightarrow \Delta S A B \text { vuông cân tại } A \Rightarrow S A=A B=a\\ &\text { Vậy thể tích của khối chóp } S . A B C \text { là: } V=\frac{1}{3} \cdot S_{A B C} \cdot S A=\frac{1}{3} \cdot \frac{a^{2} \sqrt{3}}{4} \cdot a=\frac{a^{3} \sqrt{3}}{12} \end{aligned}\)

