Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Theo giả thiết hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy suy ra \(S A \perp(A B C D)\).
Mặt khác đáy ABCD là hình vuông nên hình chóp S.ABCD chỉ có một mặt phẳng đối xứng là (SAC).
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số y =f(x) có bảng xét dấu đạo hàm như sau:

Mệnh đề nào sau đây đúng
Cho hàm số y =f(x) xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên.
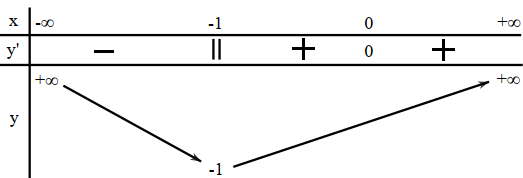
Khẳng định nào sau đây là khẳng định đúng?
Cho hàm số y \(y=f(x)\) xác định và liên tục trên khoảng \(\left(-\infty ; \frac{1}{2}\right) \text { và }\left(\frac{1}{2} ;+\infty\right)\) . Đồ thị hàm số \(y=f(x)\) là đường cong trong hình vẽ bên
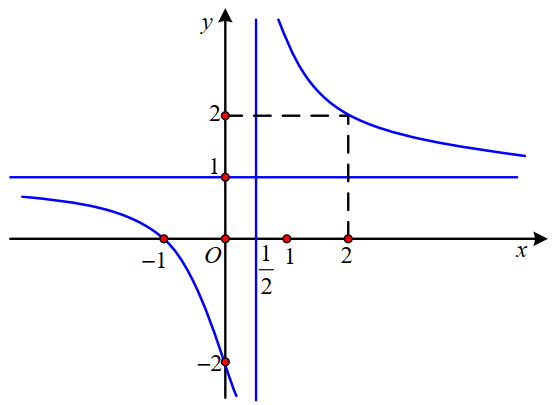
Tìm mệnh đề đúng trong các mệnh đề sau:
Cho hàm số y=f(x) có đồ thị như hình vẽ:
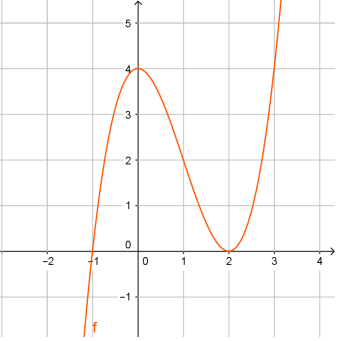
Đồ thị hàm số y=f(x) có mấy điểm cực trị?
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B , biết SA=AC=2a . Tính thể tích khối chóp S.ABC .
Cho tứ diện ABCD có AD vuông góc với mặt phẳng (ABC). Biết đáy ABC là tam giác vuông tại B và AD = 5, AB = 5, BC =12 . Tính thể tích V của tứ diện ABCD .
Cho hình chóp tứ giác đều S.ABCD với O là tâm đa giác đáy ABCD . Khẳng định nào sau đây sai?
Cho hàm số y=f(x) có bảng biến thiên:
.png)
Khẳng định nào sau đây là đúng?
Tìm giá trị nhỏ nhất m của hàm số \(y=x^{3}-3 x^{2}-9 x+5\) trên đoạn [-2;2].
Giá trị nhỏ nhất của hàm số \(f(x)=\frac{x^{2}+x+4}{x+1}\) trên đoạn [0;2] bằng
Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
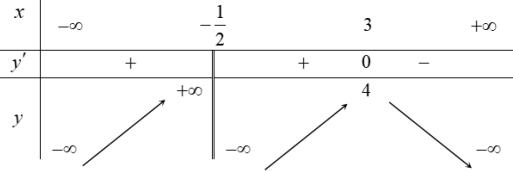
Cho hàm số y =f(x) có bảng biến thiên như hình vẽ sau:
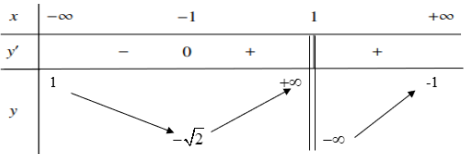
Số nghiệm của phương trình f (x)=-1 là
Hàm số \(y=x^{4}+2(m-2) x^{2}+m^{2}-2 m+3\) có đúng 1 điểm cực trị thì giá trị của m là:
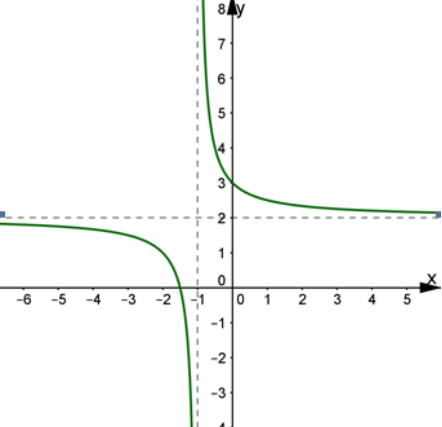
Cho hàm số f(x) có đồ thị như hình vẽ bên. Tiệm cận đứng và tiệm cận ngang của đồ thị lầnlượt là
Hàm số \(y=x^{4}-4 x^{3}+3\) đồng biến trên những khoảng nào sau đây?

