Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Chu Văn An
Đề thi giữa HK1 môn Toán 12 năm 2020 - Trường THPT Chu Văn An
-
Hocon247
-
30 câu hỏi
-
60 phút
-
87 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho hàm số \(y = \sqrt {{x^2} - 6x + 5}\). Mệnh đề nào sau đây là đúng?
\(y = \sqrt {{x^2} - 6x + 5}\)
TX Đ: \(D = ( - \infty ,1] \cup {\rm{[}}5, + \infty )\)
\(\begin{array}{l}y' = \dfrac{{x - 3}}{{\sqrt {{x^2} - 6x + 5} }}\\y' = 0 \Leftrightarrow \dfrac{{x - 3}}{{\sqrt {{x^2} - 6x + 5} }} = 0 \Leftrightarrow x = 3\\\end{array}\)
y' không xác định tại x = 1 và x = 5

Vậy hàm số đồng biến trên \(\left( {5, + \infty } \right)\)
Cho hàm số \(y = {x^4} + 4{x^2}\) có đồ thị (C). Tìm số giao điểm của đồ thị (C) và trục hoành.
\(\begin{array}{l} {x^4} + 4{x^2} = 0\\ \Leftrightarrow {x^2}\left( {{x^2} + 4} \right) = 0\\ \Leftrightarrow x = 0 \end{array}\)
Do đó đồ thị hàm số đã cho có 1 điểm chung với trục hoành.
Đồ thị sau đây là của hàm số \(y = {x^4} - 3{x^2} - 3\). Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} + m = 0\) có ba nghiệm phân biệt?
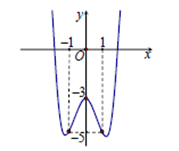
TXĐ: \(D = \mathbb{R}\)
\({x^4} - 3{x^2} + m\)
\({x^4} - 3{x^2} + m = 0\)
\(\Leftrightarrow {x^4} - 3{x^2} = - m\)
\(\Leftrightarrow {x^4} - 3{x^2} - 3 = - m - 3\)
Số nghiệm của pt \({x^4} - 3{x^2} + m = 0\) chính là số giao điểm của đths \({x^4} - 3{x^2} - 3 = 0\) và đường thẳng \(y= -m - 3\)
Từ đồ thị hàm số \(\Rightarrow - m – 3 = 0 \Leftrightarrow m=0\)
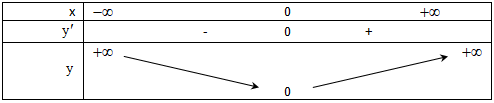
Cho hàm số y = f(x) có bảng biến thiên như sau.
Hàm số đồng biến trên khoảng nào?
Hàm số đồng biến trên khoảng (-2;3)
Biết đường thẳng \(y = - {9 \over 4}x - {1 \over {24}}\) cắt đồ thị hàm số \(y = {{{x^3}} \over 3} + {{{x^2}} \over 2} - 2x\) tại một điểm duy nhất, ký hiệu (x0 ; y0) là tọa độ điểm đó. Tìm y0.
Xét pt hoành độ gio điểm tại (x0, y0) ta có :
\(\begin{array}{l} - \dfrac{9}{4}{x_0} - \dfrac{1}{{24}} = \dfrac{{{x_0}^3}}{3} + \dfrac{{{x_0}^2}}{2} - 2{x_0}\\ \Leftrightarrow 8{x_0}^3 + 12{x_0}^2 + 6{x_0} + 1 = 0\\ \Leftrightarrow {\left( {2{x_0} + 1} \right)^3} = 0\\ \Leftrightarrow 2{x_0} + 1 = 0\\ \Leftrightarrow {x_0} = - \dfrac{1}{2} \Rightarrow {y_0} = \dfrac{{13}}{{12}}\end{array}\)
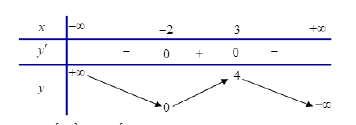
Cho hàm số y = f(x) xác định , liên tục trên R và có bảng biến thiên như dưới đây.
Đồ thị hàm số y = f(x) cắt đường thẳng y = - 2018 tại bao nhiêu điểm?
Đồ thị hàm số y = f(x) cắt đường thẳng y = - 2018 tại hai điểm phân biệt.
Trên đồ thị hàm số \(y = {{2x - 1} \over {x + 1}}\) có bao nhiêu điểm có tọa độ nguyên?
\(\begin{array}{l} y = \frac{{2x - 1}}{{x + 1}} = 2 - \frac{3}{{x + 1}}\\ x \in Z,y \in Z \Rightarrow x + 1 \in U\left( 3 \right)\\ \Rightarrow x + 1 \in \left\{ { \pm 1; \pm 3} \right\}\\ \Rightarrow x \in \left\{ { - 2;0; - 4;2} \right\} \end{array}\)
Vậy có 4 điểm có tọa độ nguyên.
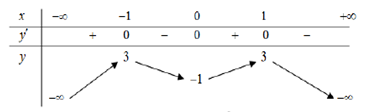
Cho hàm số y = f(x) xác định trên R\{1} và có bảng biến thiên như sau:
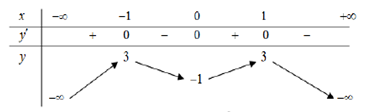
Mệnh đề nào sau đây đúng?
Hàm số không có GTNN nên A sai.
Đồ thị hàm số không có TCĐ nên B sai.
Đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt nên C đúng.
Hàm số không đồng biến trên \(\left( { - 1; + \infty } \right)\) nên D sai.
Cho hàm số có bảng biến thiên như sau:
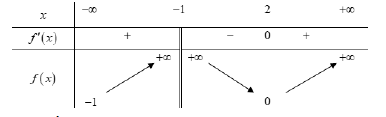
Mệnh đề nào sau đây là đúng?
Từ bbt suy ra yCT = 0.
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số \(y = {{2x - 1} \over {x + 1}}\)
\(y = \dfrac{{2x - 1}}{{x + 1}}\)
TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\)
\(\mathop {\lim }\limits_{x \to \pm \infty } \dfrac{{2x - 1}}{{x + 1}} = 2\)\(\)
TCN : y=2
\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {{( - 1)}^ + }} \dfrac{{2x - 1}}{{x + 1}} = - \infty \\\mathop {\lim }\limits_{x \to {{( - 1)}^ - }} \dfrac{{2x - 1}}{{x + 1}} = + \infty \end{array} \right\} \)
\(\Rightarrow TCĐ : x= -1\)
Hàm số \(y = {\left( {4{x^2} - 1} \right)^{ - 4}}\) có tập xác định là bao nhiêu?
Ta có: \(y = {\left( {4{x^2} - 1} \right)^{ - 4}} = \dfrac{1}{{{{\left( {4{x^2} - 1} \right)}^4}}}\)
Tập xác định là \(4{x^2} - 1 \ne 0 \Rightarrow R\backslash \left\{ { - \dfrac{1}{2};\dfrac{1}{2}} \right\}\)
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^{{{^{_\pi }} \over 2}}}\) tại điểm thuộc đồ thị có hoành độ bằng 1 là:
Gọi tiếp điểm của đồ thị hàm số là \(M\left( {1;1} \right)\)
Ta có: \(y' = \dfrac{\pi }{2}{x^{\dfrac{\pi }{2} - 1}} \Rightarrow y'\left( 1 \right) = \dfrac{\pi }{2}\)
Khi đó phương trình tiếp tuyến đó là: \(y = \dfrac{\pi }{2}\left( {x - 1} \right) + 1 \Leftrightarrow y = \dfrac{\pi }{2}x + 1 - \dfrac{\pi }{2}\)
Cho \(f(x) = \ln ({x^4} + 1)\). Đạo hàm f’(1) bằng:
Ta có: \(f'\left( x \right) = \dfrac{{4{x^3}}}{{{x^4} + 1}} \Rightarrow f'\left( 1 \right) = \dfrac{4}{2} = 2\)
Cho \({\log _2}5 = a,\,{\log _3}5 = b\). Khi đó \({\log _6}5\) tính theo a và b là bao nhiêu?
Ta có: \({\log _2}5 = a,\,{\log _3}5 = b\)
\(\Rightarrow \left\{ \begin{array}{l}{\log _5}2 = \dfrac{1}{a}\\{\log _5}3 = \dfrac{1}{b}\end{array} \right.\)
Khi đó ta có: \({\log _5}6 = {\log _5}2 + {\log _5}3 = \dfrac{1}{a} + \dfrac{1}{b} = \dfrac{{a + b}}{{ab}} \)
\(\Rightarrow {\log _6}5 = \dfrac{{ab}}{{a + b}}\)
Gọi x1, x2 là hai nghiệm của phương trình \({\log _2}^2x - 3{\log _2}x + 2 = 0\). Giá trị biểu thức \(P = {x_1}^2 + {x_2}^2\) bằng bao nhiêu?
Ta có: \({\log _2}^2x - 3{\log _2}x + 2 = 0 \)
\(\Leftrightarrow \left( {{{\log }_2}x - 1} \right)\left( {{{\log }_2} - 2} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}{\log _2}x = 1\\{\log _2}x = 2\end{array} \right.\)
\(\Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 4\end{array} \right.\)
Khi đó: \(P = {x_1}^2 + {x_2}^2 = {2^2} + {4^2} = 20.\)
Tìm tập xác định của hàm số \(y = \log \sqrt {{x^2} - x - 12}\)
Điều kiện xác định: \(\sqrt {{x^2} - x - 12} > 0 \)
\(\Leftrightarrow {x^2} - x - 12 > 0\)
\(\Leftrightarrow \left( {x + 3} \right)\left( {x - 4} \right) > 0\)
\(\Rightarrow x\; \in ( - \infty ; - 3) \cup (4; + \infty )\)
Phương trình \({49^x} - {7^x} - 2 = 0\) có nghiệm bằng bao nhiêu?
Ta có: \({49^x} - {7^x} - 2 = 0 \)
\(\Leftrightarrow {\left( {{7^x}} \right)^2} - {7^x} - 2 = 0\)
\( \Leftrightarrow \left( {{7^x} - 2} \right)\left( {{7^x} + 1} \right) = 0 \)
\(\Rightarrow {7^x} = 2 \Leftrightarrow x = {\log _7}2\)
Tìm nghiệm của bất phương trình \({3.4^x} - {5.6^x} + {2.9^x} < 0\)
Ta có: \({3.4^x} - {5.6^x} + {2.9^x} < 0 \)
\(\Leftrightarrow 2{\left( {{3^x}} \right)^2} - {5.2^x}{.3^x} + 3.{\left( {{2^x}} \right)^2} < 0\)
\( \Leftrightarrow \left( {{{2.3}^x} - {{3.2}^x}} \right)\left( {{3^x} - {2^x}} \right) < 0\)
\(\Leftrightarrow x \in \left( {0;1} \right)\)
Phương trình \({e^{2x}} - 3{e^x} - 4 + 12{e^{ - x}} = 0\) có các nghiệm nào?
Ta có: \({e^{2x}} - 3{e^x} - 4 + 12{e^{ - x}} = 0\)
\(\Leftrightarrow {e^{2x}} - 3{e^x} - 4 + \dfrac{{12}}{{{e^x}}} = 0\)
\( \Leftrightarrow {\left( {{e^x}} \right)^3} - 3\left( {{e^x}} \right){}^2 - 4\left( {{e^x}} \right) + 12 = 0\)
\(\Leftrightarrow \left( {{e^x} + 2} \right)\left( {{e^x} - 3} \right)\left( {{e^x} - 2} \right) = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}{e^x} = 3\\{e^x} = 2\end{array} \right. \)
\(\Leftrightarrow \left[ \begin{array}{l}x = \ln 3\\x = \ln 2\end{array} \right.\)
Cho a, b là các số dương thỏa mãn điều kiện: \({\log _{{2 \over 3}}}x = {1 \over 4}{\log _{{2 \over 3}}}a + {4 \over 7}{\log _{{2 \over 3}}}b\). Khi đó x nhận giá trị nào?
Ta có:
\({\log _{\dfrac{2}{3}}}x = \dfrac{1}{4}{\log _{\dfrac{2}{3}}}a + \dfrac{4}{7}{\log _{\dfrac{2}{3}}}b\) \(\Leftrightarrow {\log _{\dfrac{2}{3}}}x = {\log _{\dfrac{2}{3}}}\left( {{a^{\dfrac{1}{4}}}{b^{\dfrac{4}{7}}}} \right)\) \( \Rightarrow x = {a^{\dfrac{1}{4}}}{b^{\dfrac{4}{7}}}\)
Mệnh đề nào sau đây là mệnh đề đúng?
Số các cạnh của một hình đa diện luôn:
Tứ diện là hình đa diện đơn giản nhất có cạnh bằng 6 nên số cạnh của hình đa diện luôn lớn hơn hoặc bằng 6.
Trong các mệnh đề sau, mệnh đề nào sai?
- Khối lăng trụ tam giác, khối hộplà các khối đa diện.
- Khối tứ diện là một khối đa diện lồi.
- Không phải khi nào lắp ghép 2 khối đa diện ta cũng được khối đa diện lồi.
Chọn C.
Chú ý khi giải:
Một số em sẽ nghĩ đáp án C là đúng nhưng thực chất khi lắp ghép hai khối đa diện ta chưa chắc đã nhận được khối đa diện lồi.
Trong các kí hiệu sau, kí hiệu nào không phải của khối đa diện đều?
Có 5 khối đa diện, đó các loại \(\left\{ {3;3} \right\},\left\{ {4;3} \right\},\left\{ {3;4} \right\},\left\{ {5;3} \right\},\left\{ {3;5} \right\}\)
Vậy kí hiệu \(\left\{ {4;4} \right\}\) không phải kí hiệu của khối đa diện đều nào cả.
Cho hình chóp tứ giác đều S.ABCD có chiều cao h, góc ở đỉnh của mặt bên bằng \({60^0}.\) Thể tích hình chóp là:
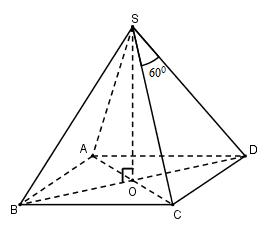
Gọi \(O = AC \cap BD\)
Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)
Đặt \(SA = SB = SC = SD = a\)
Tam giác SCD có: \(SC = SD;\widehat {CSD} = {60^0} \Rightarrow \Delta SCD\) đều \( \Rightarrow CD = SC = SD = a\)
Suy ra hình vuông ABCD cạnh \(a \Rightarrow AC = BD = a\sqrt 2 \Rightarrow OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OC \Rightarrow \Delta SOC\) vuông tại O
\(\Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \)
\(\Rightarrow h = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\) \( \Rightarrow a = h\sqrt 2 \)
\(\Rightarrow {S_{ABCD}} = {a^2} = {\left( {h\sqrt 2 } \right)^2} = 2{h^2}\)
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}h.2{h^2} = \dfrac{{2{h^3}}}{3}\)
Thể tích khối hộp chữ nhật có diện tích đáy S và độ dài cạnh bên a là:
Vì hình hộp chữ nhật cũng là hình lăng trụ nên thể tích của khối hộp cũng được tính bởi công thức V = Sh, hay V = Sa.
Bề mặt xung quanh của một hình trụ trải trên mặt phẳng là một hình vuông cạnh a. Thể tích của khối trụ giới hạn bởi hình trụ này bằng.
Gọi r là bán kính đáy của khối trụ
\(2\pi r = a \Rightarrow r = \dfrac{a}{{2\pi }}\)
h là chiều cao của khối trụ nên h = a
Thể tích khối trụ là: \(V = \pi {r^2}.h = \pi {\left( {\dfrac{a}{{2\pi }}} \right)^2}.a = \dfrac{{{a^3}}}{{4\pi }}\)
Một khối trụ tròn xoay chứa một khối cầu bán kính bằng 1. Khối cầu tiếp xúc với mặt xung quanh và hai mặt đáy của khối trụ. Thể tích khối trụ bằng
Bán kính đáy hình trụ là 1, chiều cao là 2.
Thể tích khối trụ bằng: \(V = \pi {r^2}.h = \pi {.1^2}.2 = 2\pi \)
Thể tích của khối cầu ngoại tiếp một hình hộp chữ nhật có ba kích thước \(a,\,2a,\,2a\) bằng
Bán kính khối cầu là một nửa đường chéo của hình hộp chữ nhật
\(R = \dfrac{1}{2}\sqrt {{a^2} + {{\left( {2a} \right)}^2} + {{\left( {2a} \right)}^2}} = \dfrac{3}{2}a\)
Thể tích của khối cầu ngoại tiếp hình hộp chữ nhật là:
\(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {\dfrac{3}{2}a} \right)^3} = \dfrac{9}{2}\pi {a^3}\)
Cho các mệnh đề sau:
a. Hình chóp có đáy là hình thang thì có mặt cầu ngoại tiếp.
b. Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp.
c. Hình chóp có đáy là hình chữ nhật thì có mặt cầu ngoại tiếp.
d. Hình chóp có đáy là hình thoi thì có mặt cầu ngoại tiếp.
Số mệnh đề đúng là?
Hình chóp có đáy là hình thang cân thì có mặt cầu ngoại tiếp. (Đúng)
Hình chóp có đáy là hình chữ nhật thì có mặt cầu ngoại tiếp. (Đúng)
Cho hai điểm A, B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
Tập hợp tâm các mặt cầu đi qua hai điểm A và B là mặt phẳng trung trực của đoạn thẳng AB.

