Mệnh đề nào sau đây là mệnh đề  đúng?

Số các cạnh của một hình đa diện luôn:

Cho \(f(x) = \ln ({x^4} + 1)\). Đạo hàm f’(1) bằng:

Cho hàm số \(y = \sqrt {{x^2} - 6x + 5}\). Mệnh đề nào sau đây là đúng?

Cho hàm số y = f(x) có bảng biến thiên như sau.

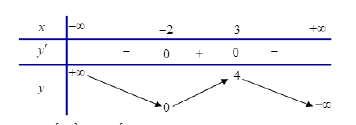
Hàm số đồng  biến trên khoảng nào?

Trên đồ thị hàm số \(y = {{2x - 1} \over {x + 1}}\) có bao nhiêu điểm có tọa độ nguyên?

Cho hàm số y = f(x) xác định trên  R\{1} và có bảng biến thiên như sau:

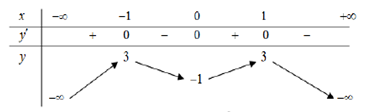
Mệnh đề nào sau đây đúng?

Thể tích khối hộp chữ nhật có diện tích đáy S và độ dài cạnh bên a là:

Cho a, b là các số dương thỏa mãn điều kiện: \({\log _{{2 \over 3}}}x = {1 \over 4}{\log _{{2 \over 3}}}a + {4 \over 7}{\log _{{2 \over 3}}}b\).  Khi đó x nhận giá trị nào?

Cho hàm số y = f(x) xác định , liên tục trên R và có bảng biến thiên như dưới đây.

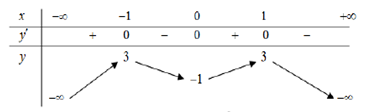
Đồ thị hàm số y = f(x) cắt đường thẳng y = - 2018 tại bao nhiêu điểm?

Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số \(y = {{2x - 1} \over {x + 1}}\)

Một khối trụ tròn xoay chứa một khối cầu bán kính bằng 1. Khối cầu tiếp xúc với mặt xung quanh và hai mặt đáy của khối trụ. Thể tích khối trụ bằng

Tìm tập xác định của hàm số \(y = \log \sqrt {{x^2} - x - 12}\)

Phương trình \({49^x} - {7^x} - 2 = 0\) có nghiệm bằng bao nhiêu?

Thể tích của khối cầu  ngoại  tiếp một hình hộp chữ nhật có ba kích thước \(a,\,2a,\,2a\) bằng

Phương trình \({e^{2x}} - 3{e^x} - 4 + 12{e^{ - x}} = 0\) có các nghiệm nào?