Do M và N lần lượt là trung điểm của BC và AC

Nên MN là đường trung bình của tam giác AB

Suy ra MN // AB \(MN = \frac{1}{2}AB\) (1)

Lại có P là trung điểm của AB

Nên \(AP = BP = \frac{1}{2}AB\) (2)

Từ (1) và (2) suy ra MN = AP = BP

Các vectơ bằng vectơ \(\overrightarrow {MN} \) là \(\overrightarrow {BP} \) và \(\overrightarrow {PA} \)

Vậy chọn B.

Nếu trong 4 điểm A, B, C, D không có ba điểm nào thẳng hàng thì ABCD tạo thành tứ giác

Thêm điều kiện \(\overrightarrow {AB} = \overrightarrow {DC}\) chứng tỏ hai cạnh AB, CD song song và bằng nhau

⇒ ABCD là hình bình hành

Vậy chọn D.

Hình thoi là tứ giác có bốn cạnh bằng nhau

Ta có:

\(\begin{array}{l} \left| {\overrightarrow {AB} } \right| = AB,\left| {\overrightarrow {BC} } \right| = BC,\left| {\overrightarrow {CD} } \right| = CD,\left| {\overrightarrow {DA} } \right| = DA\\ \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {CD} } \right| = \left| {\overrightarrow {DA} } \right| \end{array}\)

Vậy chọn B.

Hai vectơ \(\overrightarrow {BH} ,\overrightarrow {CH} \) cùng hướng.

Vậy chọn A.

Do ABCD là hình bình hành tâm O nên \(\overrightarrow {OC} = - \overrightarrow {OA} \)

Suy ra \(\overrightarrow {OB} - \overrightarrow {OA} = - \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OB} + \overrightarrow {OC} \)

Vậy chọn A.

Điểm O là trung điểm của đoạn thẳng AB

Khi và chỉ khi OA = OB và O nằm giữa A và B

Khi đó: \(\overrightarrow {OA} , \overrightarrow {OB} \) ngược hướng và có độ dài bằng nhau

Vậy chọn D.

Ta có:

\(\begin{array}{l} \overrightarrow u = \overrightarrow {AD} - \overrightarrow {CD} + \overrightarrow {CB} - \overrightarrow {AB} \\ = \left( {\overrightarrow {AD} - \overrightarrow {AB} } \right) + \left( {\overrightarrow {CB} - \overrightarrow {CD} } \right)\\ = \overrightarrow {BD} + \overrightarrow {DB} \\ = \overrightarrow 0 \end{array}\)

Vậy chọn B.

Áp dụng quy tắc hình bình hành ta có:

\(\overrightarrow {AB} + \overrightarrow {CA} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {CA} = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \)

Do đó \(\left| {\overrightarrow {AB} + \overrightarrow {CA} + \overrightarrow {AD} } \right|=0\)

Vậy chọn C.

Ta có:

\(1 = \left| {x\overrightarrow a } \right| = \left| x \right|\left| {\overrightarrow a } \right| = 2\left| x \right| \Rightarrow \left| x \right| = 0,5\)

Do \({x\overrightarrow a }\) cùng hướng với ​​\(\overrightarrow a \) nên x > 0, do đó x = 0,5

Vậy chọn B.

Do điểm B nằm giữa hai điểm A và C nên:

AB + BC = AC hay 2a + BC = 6a nên BC = 4a

Ta có BC = 2AB

Và \(\overrightarrow {BC} ,\overrightarrow {BA} \) ngược hướng nên \(\overrightarrow {BC} = - 2\overrightarrow {BA} \)

Vậy chọn D.

Do ABCDEF là lục giác đều tâm O nên AB = BC = CD = DE = EF = FA = OC

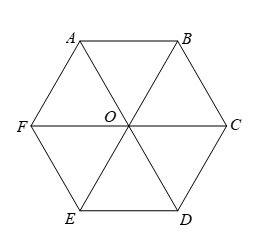
Trên hình có tất cả 12 đoạn thẳng bằng nhau và bằng OC, tạo thành 24 vectơ có độ dài bằng OC. Trừ ra vectơ \(\overrightarrow {OC} \) còn lại 23 vectơ

Vậy chọn D.

Các vectơ được tạo thành từ ba đỉnh của tam giác ABC là: \(\overrightarrow {BC} ,\overrightarrow {CB} ,\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {CA} \)

Vậy chọn A.

Gọi G là trọng tâm tam giác ABC nên: \({\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} }=3\overrightarrow {MG}\)

Để \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = k \Leftrightarrow 3\left| {\overrightarrow {MG} } \right| = k \Leftrightarrow \left| {\overrightarrow {MG} } \right| = \frac{k}{3}\)

Do đó, tập các điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = k\) là đường tròn tâm G, bán kính \(\frac k3\)

Vậy chọn B.

Từ B suy ra A là trọng tâm của tam giác A’B’C’ (vô lí).

Vậy chọn B.

Ta có:

\(\begin{array}{l} \overrightarrow {AB} = \left( {1;1} \right),\overrightarrow {BC} = \left( { - 3; - 3} \right)\\ \Rightarrow \overrightarrow {BC} = 3\overrightarrow {AB} \end{array}\)

Do đó hai vectơ này cùng phương

Vậy chọn A.

Điểm đối xứng của A(–2; 1) qua gốc tọa độ O là (2; -1).

Điểm đối xứng của A(–2; 1) qua trục tung là (2; 1)

Điểm đối xứng của A(–2; 1) qua trục hoành là (–2; –1)

Điểm đối xứng của A(–2; 1) qua H(1; 1) là M (4; 1). Khi đó, H là trung điểm AM.

Vậy chọn A.

Khi α là góc tù. Ta có:

sinα > 0

cosα < 0

tanα < 0

cotα < 0

Vậy chọn C.

Ta có: \({\overrightarrow {AB} ,\overrightarrow {DC} }\) cùng hướng nên \(\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) = {0^o}\)

\({\overrightarrow {AD} ,\overrightarrow {CB} }\) ngược hướng nên \(\left( {\overrightarrow {AD} ,\overrightarrow {CB} } \right) = {180^o}\)

Vẽ \(\overrightarrow {CE} = \overrightarrow {DC} \), khi đó

\(\left( {\overrightarrow {CO} ,\overrightarrow {DC} } \right) = \left( {\overrightarrow {CO} ,\overrightarrow {CE} } \right) = \widehat {OCE} = {135^o}\)

Do đó \(\left( {\overrightarrow {AB} ,\overrightarrow {DC} } \right) + \left( {\overrightarrow {AD} ,\overrightarrow {CB} } \right) + \left( {\overrightarrow {CO} ,\overrightarrow {DC} } \right)=315^o\)

Vậy chọn C.

\(\begin{array}{l} \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right).\overrightarrow {AD} - \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right).\overrightarrow {AB} \\ = \overrightarrow {AC} .\overrightarrow {AD} - \overrightarrow {AC} .\overrightarrow {AB} \\ = \overrightarrow {AC} \left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\\ = \overrightarrow {AC} .\overrightarrow {BD} \\ = 0 \end{array}\)

Vậy chọn A.

Ta có:

\(\begin{array}{l} \left| {\overrightarrow a } \right| = \sqrt {{1^2} + {{\left( {\sqrt 3 } \right)}^2}} = 2\\ \left| {\overrightarrow b } \right| = \sqrt {{{\left( { - 2\sqrt 3 } \right)}^2} + {6^2}} = 4\sqrt 3 \\ \overrightarrow a .\overrightarrow b = 1.\left( { - 2\sqrt 3 } \right) + \sqrt 3 .6 = 4\sqrt 3 \\ \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{4\sqrt 3 }}{{2.4\sqrt 3 }} = \frac{1}{2}\\ \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {60^o} \end{array}\)

Vậy chọn D.

Ta có:

\(\left( {\overrightarrow a - \overrightarrow b } \right)\left( {\overrightarrow a + \overrightarrow b } \right) = {\overrightarrow a ^2} - {\overrightarrow b ^2} = {\left| {\overrightarrow a } \right|^2} - {\left| {\overrightarrow b } \right|^2}\)

Vậy chọn A.

\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = 8.10.\cos {30^o} = 40\sqrt 3 \)

Vậy chọn C.

Ta có tam giác ABC vuông tại B nên \(\overrightarrow {AB} \bot \overrightarrow {BC} \Rightarrow \overrightarrow {AB} .\overrightarrow {BC} = 0\)

\(\begin{array}{l} \overrightarrow {AB} .\overrightarrow {AC} \\ = \overrightarrow {AB} .\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right)\\ = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {BC} \\ = A{B^2} + 0\\ = 81 \end{array}\)

Vậy chọn A.

Ta có: 

\(\begin{array}{l} \overrightarrow {BA} = \left( {3; - 1} \right)\\ \overrightarrow {BC} = ( - 4; - 2)\\ \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}} = \frac{{3.( - 4) + ( - 1).( - 2)}}{{\sqrt {9 + 1} .\sqrt {16 + 4} }} = - \frac{{\sqrt 2 }}{2}\\ \Rightarrow \widehat B = \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = {135^o} \end{array}\)

Vậy chọn D.

Ta có:

\(\begin{array}{l} \overrightarrow {AB} = (1;7) \Rightarrow AB = \sqrt {{1^2} + {7^2}} = 5\sqrt 2 \\ \overrightarrow {BC} = ( - 7;1) \Rightarrow BC = 5\sqrt 2 \\ \overrightarrow {CD} = ( - 1; - 7) \Rightarrow CD = 5\sqrt 2 \\ \overrightarrow {DA} = (7; - 1) \Rightarrow DA = 5\sqrt 2 \\ \Rightarrow AB = BC = CD = DA = 5\sqrt 2 \end{array}\)

Lại có:

\(\begin{array}{l} \overrightarrow {AB} .\overrightarrow {BC} = 1.( - 7) + 7.1 = 0\\ \Rightarrow AB \bot BC \end{array}\)

Từ đó suy ra ABCD là hình vuông

Vậy chọn C.

Ta có: \(P\in Ox\) nên P(x; 0)

\(\begin{array}{l} \overrightarrow {MP} = (x + 2; - 2)\\ \overrightarrow {MN} = (3; - 1) \end{array}\)

Do M, N, P thẳng hàng nên

\(\frac{{x + 2}}{3} = \frac{{ - 2}}{{ - 1}} \Leftrightarrow x = 4 \Rightarrow P(4;0)\)

Vậy chọn D.

Áp dụng định lý cosin trong tam giác ta có:

\(\begin{array}{l} B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A\\ = {4^2} + {6^2} - 2.4.6.\cos {120^o}\\ = 76\\ \Rightarrow BC = 2\sqrt {19} \end{array}\)

Vậy chọn B.

Áp dụng định lí sin trong tam giác ta có:

\(\begin{array}{l} \frac{a}{{\sin A}} = 2R\\ \Rightarrow R = \frac{a}{{2\sin {{60}^o}}} = \frac{a}{{2\frac{{\sqrt 3 }}{2}}} = \frac{{a\sqrt 3 }}{3} \end{array}\)

Vật chọn A.

Áp dụng công thức đường trung tuyến trong tam giác ta có:

\(\begin{array}{l} {m_c}^2 = \frac{{{{\left( {\sqrt {31} } \right)}^2} + {{\left( {\sqrt {29} } \right)}^2}}}{2} - \frac{{{{\left( {2\sqrt 7 } \right)}^2}}}{4} = 23\\ \Rightarrow {m_c} = \sqrt {23} \end{array}\)

Vậy chọn B.

Ta có:

\(\begin{array}{l} S = \frac{1}{2}a{h_a} \Rightarrow a = \frac{{2S}}{{{h_a}}}\\ S = \frac{1}{2}a{h_b} \Rightarrow a = \frac{{2S}}{{{h_b}}} \end{array}\)

Theo giả thiết a = 2b

Nên \(\frac{{2S}}{{{h_a}}} = 2\frac{{2S}}{{{h_b}}} \Leftrightarrow \frac{1}{{{h_a}}} = \frac{2}{{{h_b}}} \Leftrightarrow {h_b} = 2{h_a}\)

Vậy chọn A.