Đề thi giữa HK1 môn Toán 10 năm 2020 - Trường THPT Nguyễn An Ninh
-
Hocon247
-
30 câu hỏi
-
60 phút
-
54 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Mệnh đề kéo theo nào dưới đây là sai
Mọi số có chữ số tận cùng là 0 thì chia hết cho 5 nên đáp án A đúng.
Ta có: “Nếu 3 < 4 thì 3 + 1 < 4 + 1” là mệnh đề đúng nên B đúng.
Mệnh đề: “Nếu gió mùa về thì trời lạnh” là mệnh đề đúng nên C đúng.
Ta có: -4 < -3 ⇒ (-4).2 < (-3).2 ⇒ mệnh đề ở đáp án D sai.
Vậy chọn D.
Mệnh đề phủ định của mệnh đề "5 + 4 = 10" là:
Mệnh đề phủ định của mệnh đề "5 + 4 = 10" là: \(5+4\ne10\)
Vậy chọn D.
Xét tính đúng sai của mệnh đề P(n) : \(\exists n\in N*,\frac{1}{2}n\left( n+1 \right)\) chia hết cho 11".
Với n = 10 ta có \( \frac{1}{2}.10\left( 10+1 \right)=55\) chia hết cho 11 ⇒ Mệnh đề đã cho là mệnh đề đúng.
Vậy chọn B
Trong các mệnh đề sau, mệnh đề nào sai
Xét đáp án C: “Điều kiện cần và đủ để một tứ giác là hình chữ nhật là hai đường chéo bằng nhau” là mệnh đề sai vì hình thang cân cũng có hai đường chéo bằng nhau.
Vậy chọn C.
A, B, C là ba mệnh đề đúng, mệnh đề nào sau đây là đúng?
Ta có A, B, C là ba mệnh đề đúng
⇒ (A ⇒ B) đúng ⇒ C ⇒ (A ⇒ B) đúng
Vậy chọn D.
Cho tập hợp A gồm 2 phần tử. Hỏi tập hợp A có bao nhiêu tập con.
Tập hợp A có 2 phần tử nên có \(2^2=4\) tập con.
Vậy chọn A.
Tìm số phần tử của tập hợp A = {x \(\in\) Z | -3 < x \(\le\) 4}
A = {x \(\in\) Z | -3 < x \(\le\) 4} = {-2; -1; 0 ; 1; 2; 3; 4}
→ Tập hợp A có 7 phần tử
Vậy chọn B.
Cho tập A= {-1; 1; 5; 8}, B ="Gồm các ước số nguyên dương của 16". Viết tập A dưới dạng chỉ ra tính chất đặc trưng của các phần tử. Viết tập B dưới dạng liệt kê các phần tử.
Ta có: A= {-1; 1; 5; 8} ⇒ x \(\in\) {-1; 1; 5; 8} là tập nghiệm của phương trình: (x + 1)(x - 1)(x - 5)(x - 8) = 0
⇒ A = {x \(\in\) R | (x + 1)(x - 1)(x - 5)(x - 8) = 0}
B ="Gồm các ước số nguyên dương của 16"
Mà U(16) = {±1; ±2; ±4; ±8; ±16} ⇒ B = {1; 2; 4; 8; 16} .
Vậy chọn A.
Tìm số tập X thoả mãn bao hàm thức sau: {1; 2} ⊂ X ⊂ {1; 2; 3; 4; 5}
Các tập X thỏa mãn yêu cầu đề bài là: {1; 2}, {1; 2; 3}, {1; 2; 4}, {1; 2; 5}, {1; 2; 3; 4}, {1; 2; 3; 5}, {1; 2; 4; 5}, {1; 2; 3; 4; 5}
→ Có 8 tập X thỏa mãn yêu cầu đề bài
Vậy chọn A.
Trong các tập hợp sau, tập nào là tập rỗng?
\({x^2} + x - 1 = 0 \Leftrightarrow x = \frac{{ - 1 \pm \sqrt 5 }}{2} \notin Z\)
Suy ra tập \({\rm{\{ }}x \in Z|{x^2} + x - 1 = 0\}\) = Ø
Vậy chọn C.
Cho hai tập hợp A = [−1; 3) và B = [−2; −1]. Mệnh đề nào sau đây là đúng?
Ta có: A = [−1; 3) và B = [−2; −1]
⇒ A ∩ B = {−1}
Vậy chọn C.
Cho các tập hợp sau:
Tập hợp A: 'Tất cả các học sinh có học lực giỏi khối 10 của trường chuyên Trần Hưng Đạo, Bình Thuận"
Tập hợp B: "Tất cả các học sinh nữ có học lực giỏi khối 10 của trường chuyên Trần Hưng Đạo, Bình Thuận"
Tập hợp C: "Tất cả các học sinh nam có học lực giỏi khối 10 của trường chuyên Trần Hưng Đạo, Bình Thuận"
Khẳng định nào sau đây đúng?
Tập hợp A bao gồm tất cả các học sinh ở tập hợp B và C.
Khi đó ta có: C = A∖B
Vậy chọn D.
Cho các tập hợp sau:
Tập hợp A: 'Tất cả các học sinh có học lực giỏi khối 10 của trường chuyên Trần Hưng Đạo, Bình Thuận"
Tập hợp B: "Tất cả các học sinh nữ có học lực giỏi khối 10 của trường chuyên Trần Hưng Đạo, Bình Thuận"
Tập hợp C: "Tất cả các học sinh nam có học lực giỏi khối 10 của trường chuyên Trần Hưng Đạo, Bình Thuận"
Khẳng định nào sau đây đúng?
Tập hợp A bao gồm tất cả các học sinh ở tập hợp B và C.
Khi đó ta có: C = A∖B
Vậy chọn D.
Cho hai tập hợp X = {1; 2; 3; 4; 5} và Y = {−1; 0; 4}, tập hợp X ∪ Y có bao nhiêu phần tử?
Ta có: X = {1; 2; 3; 4; 5} và Y = {−1; 0; 4}
⇒ X ∪ Y = {−1; 0; 1; 2; 3; 4; 5}
Vậy chọn A.
Cho các tập hợp A = [−3; 1), B = {x ∈ R| 4 − x 2 > 0}, C = (−1; +∞). Tập hợp (A ∩ B) ∖C là:
Ta có:
4 − x 2 > 0 ⇔ x 2 − 4 < 0 ⇔ (x − 2)(x + 2) < 0 ⇔ −2 < x < 2
⇒ B = {x ∈ R| 4 − x 2 > 0} = (−2; 2)
⇒ A ∩ B = (−2; 1) ⇒ (A ∩ B) ∖C = (−2; 1) ∖ (−1; +∞) = (−2; −1]
Vậy chọn A.
Xác định các tập số sau: [−4; 3] ∖ [−2; 1]
⇒ [−4; 3] ∖ [−2; 1] = [−4; −2) ∪ (1; 3]
Vậy chọn C.
Cho hai tập hợp A = [0; 4), B = {x ∈ R/ |x| ≤ 2}. Hãy xác định khẳng định đúng nhất:
Ta có: B = {x ∈ R| |x| ≤ 2} = [−2; 2]
Suy ra:
A ∪ B = [0; 4) ∪ [−2; 2] = [−2; 4)
A ∩ B = [0; 4) ∩ [−2; 2] = [0; 2]
A∖B = [0; 4) ∖ [−2; 2] = (2; 4)
Vậy chọn D.
Cho A = (−∞; −2] , B = [3; +∞) và C = (0; 4). Khi đó (A ∪ B) ∩ C là:
(A ∪ B) ∩ C = ((−∞; −2] ∪ (0; 4)) ∩ [3; +∞) = [3; 4)
Vậy chọn C.
Cho hai tập khác rỗng: A = (m − 1; 4] , B = (−2; 2m + 2), với m ∈ R. Xác định m để A ⊂ B
Với hai tập khác rỗng: A = (m − 1; 4] , B = (−2; 2m + 2), ta có:
\(\begin{array}{l} \left\{ \begin{array}{l} m - 1 < 4\\ 2m + 2 > - 2 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m < 5\\ m > - 2 \end{array} \right. \Leftrightarrow - 2 < m < 5\begin{array}{*{20}{c}} {}&{(*)} \end{array}\\ A \subset B \Leftrightarrow \left\{ \begin{array}{l} m - 1 \ge - 2\\ 2m + 2 > 4 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m \ge - 1\\ m > 1 \end{array} \right. \Leftrightarrow m > 1 \end{array}\)
So sánh (*) ta thấy các giá trị m thỏa mãn yêu cầu là 1 < m < 5
Vậy chọn C.
Tìm tập xác định của hàm số \(y = \sqrt {x + 2} - \frac{2}{{x - 3}}\)
Hàm số xác định \( \Leftrightarrow \left\{ \begin{array}{l} x + 2 \ge 0\\ x - 3 \ne 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - 2\\ x \ne 3 \end{array} \right.\)
Vậy chọn D.
Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. TXĐ: D = R (tập đối xứng)
Ta có: f (−x) = − (−x) = x = −f (x) nên hàm số lẻ.
B. TXĐ: D = R (tập đối xứng)
Ta có: f (−x) = (−x) 2 = x 2 = f (x) nên hàm số chẵn
Vậy chọn B.
Có mấy giá trị của m để đồ thị hàm số y = x 4 − (m2 − 3m + 2) x 3 + m2 − 1 nhận trục tung làm trục đối xứng?
Ta có TXĐ: D = R (tập đối xứng)
Đồ thị hàm số đã cho nhận trục tung làm trục đối xứng hàm số đã cho là hàm số chẵn
⇔ f (−x) = f (x), ∀x ∈ R
⇔ (−x) 4 − (m2 − 3m + 2) (−x) 3 + m2 − 1 = x 4 − (m2 − 3m + 2) x 3 + m2 − 1, ∀x ∈ R
⇔ x 4 + (m2 − 3m + 2) x 3 + m2 − 1 = x 4 − (m2 − 3m + 2) x 3 + m2 − 1, ∀x ∈ R
⇔ 2 (m2 − 3m + 2) x 3 = 0, ∀x ∈ R
⇔ m2 − 3m + 2 = 0 ⇔ m = 1 hoặc m = 2.
Vậy chọn A.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số f (x) = (m + 1) x + m − 2 đồng biến trên R?
TXĐ: D = R
Hàm số f (x) = (m + 1) x + m − 2 đồng biến trên R ⇔ m + 1 > 0 ⇔ m > −1
Lại có: m ∈ Z và m ∈ [−3; 3] nên m ∈ {0; 1; 2; 3}
Vậy chọn C.
Điểm nào sau đây thuộc đồ thị hàm số \(y = \frac{1}{{x - 1}}\)
Thay lần lượt tọa độ của các điểm A, B, C, D vào hàm số \(y = \frac{1}{{x - 1}}\), ta có điểm A thuộc đồ thị hàm số.
Vậy chọn A.
Đồ thị hàm số y =ax + b đi qua hai điểm A(0; -3); B(-1; -5). Thì a và b bằng
\(\left\{ \begin{array}{l} A(0; - 3) \in y = ax + b\\ B( - 1; - 5) \in y = ax + b \end{array} \right. \Rightarrow \left\{ \begin{array}{l} - 3 = a.0 + b\\ - 5 = a.( - 1) + b \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} b = - 3\\ a = 2 \end{array} \right.\)
Vậy chọn C.
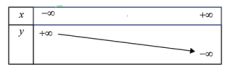
Bảng biến thiên dưới đây là của hàm số nào?
Dựa vào BBT ta thấy hàm số cần tìm nghịch biến trên
⇒ Loại đáp án A và B.
Hàm số y = 2020x - 2021 có a = 2020 > 0 nên hàm số đồng biến trên R.
⇒ Loại đáp án C.
Vậy chọn D.
Tìm m để 3 đường thẳng d1 : y = x + 1, d2 : y = 3x − 1, d3 : y = 2mx − 4m đồng quy?
Phương trình hoành độ giao điểm của d1 và d2
x + 1 = 3x − 1 ⇔ 2x = 2 ⇔ x = 1 ⇒ y = 1 + 1 = 2
Vậy d1 cắt d2 tại I(1; 2)
⇒ d1 , d2 , d3 đồng quy ⇔ I ∈ d3 ⇒ 2 = 2m.1 − 4m ⇔ m = −1
Vậy chọn B.
Đồ thị hàm số y = 3x 2 + 4x − 1 nhận đường thẳng nào dưới đây làm trục đối xứng?
Đồ thị hàm số y = 3x 2 + 4x − 1 nhận đường thẳng \(x = - \frac{4}{{2.3}} = - \frac{2}{3}\) làm trục đối xứng.
Vậy chọn C.
Hàm số y = −x 2 + 2x + 3 có đồ thị là hình nào trong các hình sau?
Hàm số y = −x 2 + 2x + 3 có a = -1 < 0 ⇒ đồ thị hàm số có bề lõm quay xuống dưới
⇒ Loại C.
Đồ thị hàm số đã cho có đỉnh I(1; 4)
Vậy chọn B.
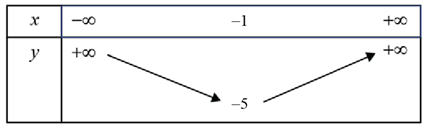
Cho parabol y = f (x) = ax 2 + bx + c (a ≠ 0) có bảng biến thiên như hình dưới đây
Đỉnh của parabol là điểm:
Từ bảng biến thiên ta suy ra đỉnh của parabol là điểm I (−1; −5)
Vậy chọn B.