Đề thi giữa HK2 môn Toán 7 năm 2021 - Trường THCS Khánh Bình
-
Hocon247
-
40 câu hỏi
-
60 phút
-
34 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Mệnh đề: “Tổng của hai số hữu tỉ nghịch đảo của nhau” được biểu thị bởi
Gọi số hữu tỉ bất kì là a(a≠0) thì số nghịch đảo của nó là \(\frac{1}{a}\)
Mệnh đề: “Tổng của hai số hữu tỉ nghịch đảo của nhau” được biểu thị bởi \(a + \frac{1}{a}\left( {a \in Q;{\mkern 1mu} a \ne 0} \right)\)
Minh mua 4 cuốn sách Toán mỗi cuốn giá x đồng và 3 cuốn sách Văn mỗi cuốn giá y đồng. Biểu thức biểu thị số tiền Minh phải trả là:
Số tiền Minh phải trả cho 4 cuốn sách Toán là 4x (đồng)
Số tiền Minh phải trả cho 3 cuốn sách Văn là 3y (đồng)
Minh phải trả tất cả số tiền là 4x+3y (đồng)
Nam mua 10 quyển vở, mỗi quyển giá x đồng và hai bút bi, mỗi chiếc giá y đồng. Biểu thức biểu thị số tiền Nam phải trả là:
Số tiền Nam phải trả cho 10 quyển vở là 10x (đồng)
Số tiền Nam phải trả cho 2 chiếc bút bi là 2y (đồng)
Nam phải trả tất cả số tiền là 10x+2y(đồng)
Đáp án cần chọn là: D
Biểu thức a2 + b3 được phát biểu bằng lời là:
Biểu thức a2+b3 được phát biểu bằng lời là “Tổng của bình phương của a và lập phương của b.”
Biểu thức a - b3 được phát biểu bằng lời là:
Biểu thức a−b3 được phát biểu bằng lời là “hiệu của a và lập phương của b"
Mệnh đề: “Tổng các bình phương của ba số a, b và c” được biểu thị bởi
Tổng các bình phương của ba số a, b và c là \( a^2+b^2+c^2\)
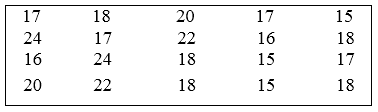
Số lượng học sinh nữ của một lớp trong một trường Trung học cơ sở được ghi nhận trong bảng sau.
Có bao giá trị khác nhau của dấu hiệu?
Có 7 giá trị khác nhau của dấu hiệu, đó là : 15;16;17;18;20;22;24.
Số lượng học sinh giỏi trong từng lớp của một trường trung học cơ sở được ghi lại bởi bảng dưới đây
.png)
Dấu hiệu cần tìm hiểu ở đây là gì?
Dấu hiệu là số học sinh giỏi trong mỗi lớp
Tính giá trị của biểu thức \(A=2 x^{2}-\frac{1}{2} y \text { tại } x=2 ; y=9\)
Thay x=2 ; y=9 vào biểu thức \(A=2 x^{2}-\frac{1}{2} y\) ta có
\(A=2.2^{2}-\frac{1}{2} \cdot 4=6\)
Cho biểu thức đại số \(Q(x)=x^{4}+4 x^{3}+2 x^{2}-4 x+1\). Tính \(Q(-2)\)
Ta có \(Q(-2)=(-2)^{4}+4(-2)^{3}+2(-2)^{2}-4(-2)+1=1\)
Cho biểu thức \(P(x)=x^{4}+2 x^{2}+1\). Tính \(P\left(\frac{1}{2}\right)\)
Ta có \(P\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{4}+2\left(\frac{1}{2}\right)^{2}+1=\frac{25}{16}\)
Cho biểu thức \(P(x)=x^{4}+2 x^{2}+1\). Tính P(-1)
Ta có \(P(-1)=(-1)^{4}+2(-1)^{2}+1=4\)
Giá trị của biểu thức \(\mathrm{D}=\mathrm{xy}-\frac{1}{2} \mathrm{x}^{2} \mathrm{y}^{3}+2 \mathrm{xy}-2 \mathrm{x}+\frac{1}{2} \mathrm{x}^{2} \mathrm{y}^{3}+\mathrm{y}+1 \quad \text { tại } \mathrm{x}=0,1 \text { và } \mathrm{y}=-2\) là
Ta có
\({\rm{D}} = {\rm{xy}} - \frac{1}{2}{{\rm{x}}^2}{{\rm{y}}^3} + 2{\rm{xy}} - 2{\rm{x}} + \frac{1}{2}{{\rm{x}}^2}{{\rm{y}}^3} + {\rm{y}} + 1 = \left( {xy + 2xy} \right) + \left( { - \frac{1}{2}{x^2}{y^3} + \frac{1}{2}{x^2}{y^3}} \right) - 2x + y + 1 = 3xy - 2x + y + 1\)
Thay \(\mathrm{x}=0,1 \text { và } \mathrm{y}=-2\) vào \(3 x y-2 x+y+1\) ta được
\(\begin{array}{l} D = {\rm{3 }}{\rm{.0,1}}{\rm{. }}\left( { - 2} \right){\rm{ - 2 }}{\rm{.0,1 + }}\left( { - 2} \right){\rm{ + 1}}\\ {\rm{ = - }}\frac{9}{5} \end{array}\)
Giá trị của biểu thức \(\begin{aligned} &C=0,25 x y^{2}-3 x^{2} y-5 x y-x y^{2}+x^{2} y+0,5 x y\text { tại } x=0,5 \text { và } y=-1 \end{aligned}\) là:
Thay \(x=0,5 \text { và } y=-1\) vào biểu thức ta có
\(\begin{array}{l} C = 0,25.0,5.{\left( { - 1} \right)^2} - 3{\left( {0,5} \right)^2}.\left( { - 1} \right) - 5.0,5.\left( { - 1} \right) - 0,5.{\left( { - 1} \right)^2} + {\left( {0,5} \right)^2}\left( { - 1} \right) + 0,5.0,5.\left( { - 1} \right)\\ = \frac{{19}}{8} \end{array}\)
Một cửa hàng đem cân một số bao gạo (đơn vị kilogam), kết quả được ghi lại ở bảng sau:
.png)
Có bao nhiêu bao gạo cân nặng lớn hơn 50 kg
Từ bảng tần số ta thấy có 88 bao có khối lượng 55kg; 44 bao có khối lượng 60kg và 11 bao có khối lượng 65kg
Nên có 8+4+1=13 bao gạo có khối lượng lớn hơn 50kg.
Đáp án cần chọn là: A
Điều tra về sự tiêu thụ điện năng (tính theo kwh) của một số gia đình ở một tổ dân phố, ta có kết quả sau:
.png)
Dấu hiệu cần tìm hiểu ở đây là gì?
Dấu hiệu: Sự tiêu thụ điện năng (tính theo kwh) của một số gia đình ở một tổ dân phố.
Bậc của đơn thức \(J=\left(-2 x y^{2}\right)^{n-1} \cdot 3 x \cdot\left(4 x^{2} y\right)^{n+1} \cdot(2 x y z)^{2 n+1}\) là
Ta có
\(\begin{array}{l} J=\left(-2 x y^{2}\right)^{n-1} \cdot 3 x \cdot\left(4 x^{2} y\right)^{n+1} \cdot(2 x y z)^{2 n+1} \\ =(-1)^{n} \cdot 2^{n-1} \cdot x^{n-1} \cdot y^{2(n-1)} \cdot 3 x \cdot 4 \cdot^{n+1} x^{2(n+1)} y^{n+1} \cdot 2^{2(n+1)} \cdot x^{2 n+1} \cdot y^{2 n+1} \cdot z^{2 n+1} \\ =(-1)^{n-1} \cdot 3 \cdot 2^{n-1+2 n+1+2(n+1)} \cdot x^{n-1+1+2(n+1)+2 n+1} \cdot y^{2(n-1)+n+1+2 n+1} \cdot z^{2 n+1} \\ =3 \cdot(-1)^{n-1} \cdot 2^{3 n+2(n+1)} x^{5 n+3} y^{5 n} z^{2 n+1} \\ =3 \cdot(-1)^{n-1} \cdot 2^{5 n+2} x^{5 n+3} y^{5 n} z^{2 n+1} \end{array}\)
Bậc của đơn thức J là \(5 n+3+5 n+2 n+1=12 n+4\)
Thu gọn đơn thức \(J=\left(-2 x y^{2}\right)^{n-1} \cdot 3 x \cdot\left(4 x^{2} y\right)^{n+1} \cdot(2 x y z)^{2 n+1}\) ta được
Ta có
\(\begin{array}{*{20}{l}} \begin{array}{l} J = {\left( { - 2x{y^2}} \right)^{n - 1}} \cdot 3x \cdot {\left( {4{x^2}y} \right)^{n + 1}} \cdot {(2xyz)^{2n + 1}}\\ = {\left( { - 1} \right)^n}{.2^{n - 1}}.{x^{n - 1}}.{y^{2\left( {n - 1} \right)}}.3x{.4.^{n + 1}}{x^{2\left( {n + 1} \right)}}{y^{n + 1}}{.2^{2\left( {n + 1} \right)}}.{x^{2n + 1}}.{y^{2n + 1}}.{z^{2n + 1}}\\ = {( - 1)^{n - 1}} \cdot 3 \cdot {2^{n - 1 + 2n + 1 + 2\left( {n + 1} \right)}} \cdot {x^{n - 1 + 1 + 2(n + 1) + 2n + 1}} \cdot {y^{2(n - 1) + n + 1 + 2n + 1}}.{z^{2n + 1}} \end{array}\\ \begin{array}{l} = 3 \cdot {( - 1)^{n - 1}} \cdot {2^{3n + 2(n + 1)}}{x^{5n + 3}}{y^{5n}}{z^{2n + 1}}\\ = 3 \cdot {( - 1)^{n - 1}} \cdot {2^{5n + 2}}{x^{5n + 3}}{y^{5n}}{z^{2n + 1}} \end{array} \end{array}\)
Bậc của đơn thức \(I=\left(x y^{2} z\right)^{n} \cdot x^{n+1} \cdot 2\left(y z^{2}\right)^{n-1}\) là
Ta có
\(\begin{array}{l} I=\left(x y^{2} z\right)^{n} \cdot x^{n+1} \cdot 2\left(y z^{2}\right)^{n-1} \\ =x^{n} y^{2 n} z^{n} \cdot x^{n+1} \cdot 2 y^{n-1} z^{2(n-1)} \\ =2 \cdot x^{n} \cdot x^{n+1} \cdot y^{2 n} \cdot y^{n-1} \cdot z^{2 n-2} \\ =2 x^{2 n+1} y^{3 n-1} z^{2 n-2} \end{array}\)
Bậc của đơn thức là \(2 n+1+3 n-1+2 n-2=7 n-2\)
Thu gọn đơn thức \(I=\left(x y^{2} z\right)^{n} \cdot x^{n+1} \cdot 2\left(y z^{2}\right)^{n-1}\) ta được
Ta có
\(\begin{array}{l} I = {\left( {x{y^2}z} \right)^n} \cdot {x^{n + 1}} \cdot 2{\left( {y{z^2}} \right)^{n - 1}}\\ = {x^n}{y^{2n}}{z^n} \cdot {x^{n + 1}} \cdot 2{y^{n - 1}}{z^{2(n - 1)}}\\ = 2 \cdot {x^n} \cdot {x^{n + 1}} \cdot {y^{2n}} \cdot {y^{n - 1}} \cdot {z^{2n - 2}}\\ = 2{x^{2n + 1}}{y^{3n - 1}}{z^{2n - 2}} \end{array}\)
Bậc của đơn thức \(H=x y^{2} z^{3} \cdot(2 x y z)^{3} \cdot 3 x^{2}(2 x y)^{3}\) là
Ta có
\(\begin{array}{l} H=x y^{2} z^{3} \cdot(2 x y z)^{3} \cdot 3 x^{2}(2 x y)^{3}=x y^{2} z^{3} \cdot 8 x^{3} y^{3} z^{3} \cdot 3 x^{2} \cdot 8 x^{3} y^{3} \\ =8.3 .8 \cdot x \cdot x^{3} \cdot x^{3} \cdot y^{2} \cdot y^{3} \cdot y^{3} \cdot z^{3} \cdot z^{3}=192 x^{7} y^{8} z^{6} \end{array}\)
Bậc của H là 7+8+6=21
Thu gọn đơn thức \(H=x y^{2} z^{3} \cdot(2 x y z)^{3} \cdot 3 x^{2}(2 x y)^{3}\) ta được
Ta có
\(\begin{array}{l} H = x{y^2}{z^3} \cdot {(2xyz)^3} \cdot 3{x^2}{(2xy)^3} = x{y^2}{z^3} \cdot 8{x^3}{y^3}{z^3} \cdot 3{x^2} \cdot 8{x^3}{y^3}\\ = 8.3.8 \cdot x \cdot {x^3} \cdot {x^3} \cdot {y^2} \cdot {y^3} \cdot {y^3} \cdot {z^3} \cdot {z^3} = 192{x^7}{y^8}{z^6} \end{array}\)
Tổng các đơn thức 3x2y4 và 7x2y4 là
Ta có : 3x2y4 + 7x2y4 = 10x2y4
Chọn đáp án B
Đơn thức đồng dạng với đơn thức 32x2y3 là:
Đơn thức đồng dạng với đơn thức 3x2y3 là -7x2y3 vì hai đơn thức này có chung phần biến x2y3 và có hệ số khác 0.
Chọn đáp án B
Đơn thức nào sau đây đồng dạng với đơn thức \(5 x^{2} y\) là
Ta thấy đơn thức \(7 x^{2} y\) có phần biến giống với đơn thức đã cho nên là đơn thức đồng dạng.
Điền đơn thức thích hợp vào chỗ trống \(-7 x^{2} y z^{3}-\cdots=-11 x^{2} y z^{3}\)
Ta có
\(-7 x^{2} y z^{3}-\left(-11 x^{2} y z^{3}\right)=-7 x^{2} y z^{3}+11 x^{2} y z^{3}=4 x^{2} y z^{3}\)
Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”
Định lý: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy
Số cần điền là 2/3.
Chọn đáp án A.
Chọn câu sai:
Một tam giác chỉ có một trọng tâm nên D sai.
Chọn đáp án D.
ΔABC có AB = 4cm, AC = 2cm. Biết độ dài BC là một số nguyên chẵn. Vậy BC bằng
Áp dụng bất đẳng thức trong tam giác ABC ta có: AB – AC < BC < AB + AC
Thay số: 4 – 2 < BC < 4 + 2
Suy ra: 2 < BC < 6
Mà độ dài cạnh BC là một số nguyên chẵn, vậy BC = 4 cm.
Chọn đáp án B
Cho tam giác ABC có M là một điểm nằm trong tam giác ABC, BM cắt AC tại D. Khi đó
.png)
Vì M là điểm nằm trong tam giác ABC và BM cắt AC tại D nên M nằm giữa hai điểm B và D
Nên ta có: BD = BM + MD
Trong tam giác MDC ta có:
MC < MD + DC (bất đẳng thức trong tam giác)
MB + MC < MB + MD + DC
MB + MC < (BM + MD) + DC
MB + MC < BD + DC
Vậy MB + MC < DB + DC.
Chọn đáp án B
Độ dài hai cạnh của một tam giác là 2 cm và 10 cm. Trong các số đo sau đây, số đo nào là độ dài cạnh thứ ba của tam giác đó.
Gọi độ dài cạnh thứ ba của tam giác là x cm (x > 0)
Áp dụng bất đẳng thức trong tam giác ta có: 10 – 2 < x < 10 + 2
Hay 8 < x < 12
Trong bốn đáp án A, B, C, D thì đáp án D thỏa mãn vì 8 < 9 < 12
Vậy độ dài cạnh thứ ba là 9 cm.
Chọn đáp án C
Chọn câu trả lời đúng. Ba cạnh của tam giác có độ dài là 6cm; ,7cm; ,8cm. Góc lớn nhất là góc
Vì trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn mà cạnh 8cm là cạnh lớn nhất trong tam giác nên góc lớn nhất là góc đối diện với cạnh có độ dài 8cm.
Cho tam giác ABC có \( \widehat A = {50^0};\widehat B = {70^0}\) . Em hãy chọn câu trả lời đúng nhất.
.png)
Áp dụng định lí tổng ba góc của một tam giác vào ΔABC ta có: \( \hat A + \hat B + \hat C = {180^0}\)
\( \to \widehat C = {180^0} - \widehat A - \widehat B = {60^0} \to \widehat A < \widehat C < \widehat B \to BC < AB < AC\)
Cho tam giác ABC có \( \widehat B = {95^0},\widehat A = {40^0}\) Em hãy chọn câu trả lời đúng nhất.
.png)
Xét ΔABC có: \( \widehat A + \widehat B + \widehat C = {180^0}\)
(định lý tổng ba góc trong tam giác)
\( \Rightarrow \hat C = {180^0} - \hat A - \hat B = {180^0} - {40^0} - {95^0} = {45^0}\)
\( \to \widehat A < \widehat C < \widehat B \to BC = AB = AC\)
Cho \(\Delta MNP\) có MN < MP < NP. Trong các khẳng định sau, câu nào đúng?
Vì ΔMNP có MN \(\hat P < \hat N < \hat M\)
Cho \( \Delta ABC\) có AC > BC > AB. Trong các khẳng định sau, câu nào đúng?
Vì ΔABC có AC>BC>AB nên theo quan hệ giữa cạnh và góc trong tam giác ta có \( \hat C < \hat A < \hat B\)
Ba cạnh của tam giác có độ dài là 9cm; ,15cm; ,12cm Góc nhỏ nhất là góc
Vì trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn mà cạnh 9cm là cạnh nhỏ nhất trong tam giác nên góc nhỏ nhất là góc đối diện với cạnh có độ dài 9cm.
Đơn thức nào không đồng dạng với đơn thức \(\left(-5 x^{2} y^{2}\right)(-2 x y)\)
Ta có \(\left(-5 x^{2} y^{2}\right)(-2 x y)=10 x^{3} y^{3}\)
\(2 x\left(-5 x^{2} y^{2}\right)=-10x^3y^2\)
Hai đơn thức trên không đồng dạng với nhau vì có phần biến khác nhau.
Bậc của đơn thức \(G=x\left[\frac{2}{9} y\left(3 x y^{2}\right)^{2}\right]^{3}\) là
Ta có \(G=x\left[\frac{2}{9} y\left(3 x y^{2}\right)^{2}\right]^{3}=x\left(\frac{2}{9} y .9 x^{2} y^{4}\right)^{3}=x \cdot\left(2 x^{2} y^{5}\right)^{3}=x .8 \cdot x^{6} \cdot y^{12}=8 x^{7} y^{12}\)
Bậc của G là 7+12=19
Giá trị của biểu thức \(\begin{aligned} &C=0,25 x y^{2}-3 x^{2} y-5 x y-x y^{2}+x^{2} y+0,5 x y\text { tại } x=0,5 \text { và } y=-1 \end{aligned}\) là:
Thay \(x=0,5 \text { và } y=-1\) vào biểu thức ta có
\(\begin{array}{l} C = 0,25.0,5.{\left( { - 1} \right)^2} - 3{\left( {0,5} \right)^2}.\left( { - 1} \right) - 5.0,5.\left( { - 1} \right) - 0,5.{\left( { - 1} \right)^2} + {\left( {0,5} \right)^2}\left( { - 1} \right) + 0,5.0,5.\left( { - 1} \right)\\ = \frac{{19}}{8} \end{array}\)