Đề thi giữa HK1 môn Toán 10 năm 2020 - Trường THPT Thủ Đức
-
Hocon247
-
30 câu hỏi
-
60 phút
-
58 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai?
Có 5 vectơ mà điểm đầu là O, điểm cuối là đỉnh của ngũ giác: \(\overrightarrow {OA} ,\overrightarrow {OB} ,\overrightarrow O C,\overrightarrow {OD} ,\overrightarrow {OE} \)
Các vectơ này có độ dài bằng nhau (tính chất của các đa giác đều).
Các vectơ khác \(\overrightarrow {0} \) có điểm đầu và điểm cuối là các đỉnh, giá là các cạnh của ngũ giác có độ dài bằng nhau, bằng cạnh của ngũ giác đều.
Vậy các phương án A, B, D đều đúng, phương án C sai.
Vì có 5 vectơ mà điểm đầu là A, điểm cuối là đỉnh của ngũ giác: \(\overrightarrow {AA} ,\overrightarrow {AB} ,\overrightarrow {AC},\overrightarrow {AD} ,\overrightarrow {AE} \).
Cho tam giác đều ABC với đường cao AH. Đẳng thức nào sau đây đúng?
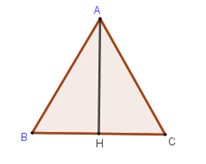
Do tam giác ABC là tam giác đều nên đường cao AH là trường trung tuyến.
⇒ H là trung điểm BC ⇒ \(BH=HC=\frac{BC}{2}\)
Lại có AC = BC nên AC = 2HC (1)
Mà \(\left| \overrightarrow{AC} \right|=AC;\left| \overrightarrow{HC} \right|=HC\)
Từ (1) và (2) suy ra \(\left| {\overrightarrow {AC} } \right| = 2\left| {\overrightarrow {HC} } \right|\)
Vậy chọn đáp án B.
Cho tam giác ABC. Vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) có giá chứa đường thẳng nào sau đây?
Dựng hình bình hành ABCD.
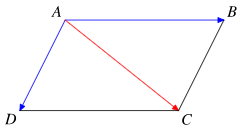
Theo quy tắc hình bình hành, ta có \(\overrightarrow {AB} + \overrightarrow {AC} =\overrightarrow {AD} \).
Vì AD chứa đường trung tuyến AE của tam giác ABC, do đó \(\overrightarrow {AB} + \overrightarrow {AC} \) có giá chứa đường trung tuyến qua A.
Vậy chọn C.
Cho hình vuông ABCD cạnh a, \(\left| {\overrightarrow {AB} + \overrightarrow {CA} + \overrightarrow {AD} } \right|\) bằng
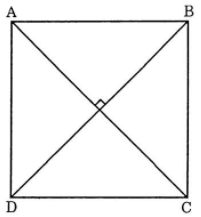
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow {AB} + \overrightarrow {CA} + \overrightarrow {AD} = \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \overrightarrow {CA} = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \)
Do đó \(\left| {\overrightarrow {AB} + \overrightarrow {CA} + \overrightarrow {AD} } \right| = 0\)
Vậy chọn đáp án B.
Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \). Biết rằng B nằm giữa A và C. Giá trị k thỏa mãn điều kiện nào sau đây?
Vì B nằm giữa A và C nên \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng hướng và AB < AC nên 0 < k < 1.
Vậy chọn đáp án C.
Cho tam giác ABC và điểm M thỏa mãn \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \). Khi đó điểm M là:
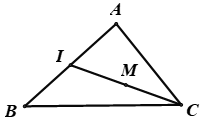
Gọi I là trung điểm AB.
Khi đó với mọi M ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
\(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {MI} + 2\overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {MI} + \overrightarrow {MC} = \overrightarrow 0 \)
⇒ M là trung điểm của CI.
Vậy chọn đáp án D.
Cho tam giác ABC. Tập hợp các điểm M sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} + \overrightarrow {MD} } \right|\) là
Gọi E, F lần lượt là trung điểm của AB, AC.
Khi đó ta có:
\(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} + \overrightarrow {MD} } \right|\)
\( \Leftrightarrow \left| {2\overrightarrow {ME} } \right| = \left| {2\overrightarrow {MF} } \right|\)
\( \Leftrightarrow \left| {\overrightarrow {ME} } \right| = \left| {\overrightarrow {MF} } \right|\)
Do đó M thuộc đường trung trực của EF.
Vậy chọn đáp án C.
Cho ba điểm M(2; 2), N( - 4; - 4), P(5; 5). Khẳng định nào sau đây đúng?
Ta có: \(\overrightarrow {MN} \left( { - 6; - 6} \right),\overrightarrow {MP} \left( {3;3} \right)\)
Suy ra \(\overrightarrow {MN} = - 2\overrightarrow {MP} \)
Nên M nằm giữa N và P
Vậy chọn đáp án A.
Trong mặt phẳng tọa độ Oxy cho các điểm A(3; 1); B(2; 2); C(1; 16); D(1; –6). Hỏi G(2; –1) là trọng tâm của tam giác nào trong các tam giác sau đây?
Ta có:
\(\left\{ \begin{gathered} {x_G} = \frac{{{x_A} + {x_B} + {x_D}}}{3} = \frac{{3 + 2 + 1}}{3} = 2 \hfill \\ {y_G} = \frac{{{y_A} + {y_B} + {y_D}}}{3} = \frac{{1 + 2 + ( - 6)}}{3} = - 1 \hfill \\ \end{gathered} \right.\)
Nên G là trọng tâm tam giác ABD.
Vậy chọn đáp án A.
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Khi đó ABCD là hình bình hành nếu
Nếu \(\overrightarrow {MN} = \overrightarrow {AB} \) và \(\overrightarrow {MN} = \overrightarrow {DC} \) thì \(\overrightarrow {AB} = \overrightarrow {DC} \)
Do đó ABCD là hình bình hành.
Vậy chọn đáp án D.
Cho hình bình hành ABCD. Tập hợp tất cả các điểm M thỏa mãn đẳng thức \(\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {MD} \) là
Ta có:
\(\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {MD} \Leftrightarrow \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {MD} - \overrightarrow {MA} \Leftrightarrow \overrightarrow {CB} = \overrightarrow {AD} \) (vô lí)
⇒ Không có điểm M.
Vậy chọn đáp án A.
Cho tam giác ABC với AB = c, BC = a, CA = b. Gọi CM là đường phân giác trong của góc C (M∈AB). Biểu thị nào sau đây là đúng?
Áp dụng tính chất của đường phân giác ta có:
\(\frac{{MA}}{{MB}} = \frac{{AC}}{{BC}} \Rightarrow MA = \frac{{AC}}{{BC}}MB\)
⇒ \(\overrightarrow {MA} = - \frac{b}{a}\overrightarrow {MB} \)
Vậy chọn đáp án B.
Cho hình vuông ABCD cạnh a, tâm O. Tính \(\left| {\overrightarrow {OA} + \overrightarrow {OC} } \right|\)?
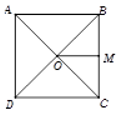
Gọi M là trung điểm của BC.
Tam giác ABC có: O, M lần lượt là trung điểm của AC, BC.
Nên OM là đường trung bình của tam giác.
Suy ra AB = 2OM
Ta có: \(\left| {\overrightarrow {OA} + \overrightarrow {OC} } \right|=2|\overrightarrow {OM}|=2OM=AB=a \)
Vậy chọn đáp án A.
Cho ba vectơ \(\overrightarrow a = \left( {2;1} \right),\overrightarrow b = \left( {3;4} \right),\overrightarrow c = \left( {7;2} \right)\). Giá trị của k, h để \(\overrightarrow c = k.\overrightarrow a + h.\overrightarrow b \) là
Ta có:
\(\left. \begin{gathered} k\overrightarrow a = (2k;k) \hfill \\ h\overrightarrow b = \left( {3h;4h} \right) \hfill \\ \end{gathered} \right\} \Rightarrow k\overrightarrow a + h\overrightarrow b = \left( {2k + 3h;k + 4h} \right)\)
Theo đề bài:
\(\overrightarrow c = k\overrightarrow a + h\overrightarrow b \Leftrightarrow \left\{ \begin{gathered} 7 = 2k + 3h \hfill \\ 2 = k + 4h \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} k = 4,4 \hfill \\ h = - 0,6 \hfill \\ \end{gathered} \right.\)
Vậy chọn đáp án C.
Cho các vectơ \(\overrightarrow a = ( - 1;2),\overrightarrow b = (3;5)\). Tìm các số thực x, y sao cho \(x\overrightarrow a + y\overrightarrow b = \overrightarrow 0 \)
Do \(\overrightarrow a ,\overrightarrow b \) là các vectơ không cùng phương nên \(x\overrightarrow a + y\overrightarrow b = \overrightarrow 0 \)⇔ x = y = 0
M là điểm trên nửa đường trong lượng giác sao cho góc xOM = α. Tọa độ của điểm M là
Vì tung độ của điểm M là sin α, hoành độ của M là cos α nên M(cos α; sin α).
Tính giá trị biểu thức P = sin30°cos15° + sin150°cos165°.
Hai góc 30o và 150o bù nhau nên sin30o = sin 150o
Hai góc 15o và 165o bù nhau nên cos 15o = cos 165o.
Do đó P = sin30°cos15° + sin150°cos165° = sin30°cos15° + sin30°(-cos15°) = 0.
Vậy chọn đáp án C.
Cho biết \(\sin \frac{\alpha }{3} = \frac{3}{5}\). Giá trị của \(P = 3{\sin ^2}\frac{\alpha }{3} + 5{\cos ^2}\frac{\alpha }{3}\) bằng bao nhiêu?
Ta có: \({\sin ^2}\frac{\alpha }{3} + {\cos ^2}\frac{\alpha }{3} = 1 \Leftrightarrow {\cos ^2}\frac{\alpha }{3} = 1 - {\sin ^2}\frac{\alpha }{3} = \frac{{16}}{{25}}\)
Do đó ta có:
\(P = 3{\sin ^2}\frac{\alpha }{3} + 5{\cos ^2}\frac{\alpha }{3}=3.{\left( {\frac{3}{5}} \right)^2} + 5.\frac{{16}}{{25}} = \frac{{107}}{{25}}\)
Vậy chọn đáp án B.
Cho tam giác đều ABC có đường cao AH. Tính \(\left( {\overrightarrow {AH} ,\overrightarrow {BA} } \right)\)
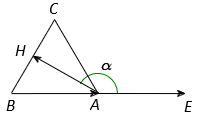
Vẽ \(\overrightarrow {AE} = \overrightarrow {BA} \).
Vì tam giác ABC là tam giác đều nên đồng thời AH là đường phân giác.
Suy ra \(\widehat {BAH} = \frac{1}{2}\widehat {BAC} = {30^o}\)
Khi đó \(\left( {\overrightarrow {AH} ,\overrightarrow {BA} } \right) = \widehat {HAE} = {180^o} - \widehat {BAH} = {180^o} - {30^o} = {150^o}\)
Vậy chọn đáp án D.
Trong mặt phẳng tọa độ Oxy, cho A(2; 1), B(3; -2), C(5; 7). Giá trị của \(\overrightarrow {AB} .\overrightarrow {AC} \) là:
Ta có:
\(\begin{gathered} \overrightarrow {AB} = (1; - 3),\overrightarrow {AC} = (3;6) \hfill \\ \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 1.3 + ( - 3).6 = - 15 \hfill \\ \end{gathered} \)
Vajayc họn đáp án B.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 1), B(4; 13), C(5; 0). Tọa độ trực tâm H của tam giác ABC là
Ta có:
\(\begin{gathered} \overrightarrow {AB} = (3;12),\overrightarrow {AC} = (4; - 1) \hfill \\ \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = 3.4 + 12.( - 1) = 0 \hfill \\ \end{gathered} \)
⇒ Tam giác ABC vuông tại A.
Nên trực tâm của tam giác là đỉnh A.
Vậy chọ đáp án B.
Cho hình vuông ABCD cạnh a. Giá trị của \(\overrightarrow {AB} .\overrightarrow {AC} \) là
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Ta có:
\(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^o}\)
\(\Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos {45^o} = a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2}\)
Vậy chọn đáp án A.
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow a = (1; - 3),\overrightarrow b = (6,x)\). Hai vectơ đó vuông góc với nhau khi và chỉ khi
Ta có:
\(\overrightarrow a .\overrightarrow b = 1.6 - 3x = 6 - 3x\)
Hai vectơ này vuông góc với nhau khi \(\overrightarrow a .\overrightarrow b = 0 \Leftrightarrow 6 - 3x = 0 \Leftrightarrow x = 2\)
Vậy chọn đáp án B.
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = (4;3),\overrightarrow b = (1;7)\). Tính góc giữa hai vectơ \(\overrightarrow a ,\overrightarrow b \).
Ta có
\(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a ,\overrightarrow b }}{{\left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|}} = \frac{{4.1 + 3.7}}{{\sqrt {16 + 9} \sqrt {1 + 49} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {45^o}\)
Vậy chọn đáp án D.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4); B(3; 2); C(5; 4). Tính chu vi P của tam giác đã cho.
Ta có:
\(\left\{ \begin{gathered} \overrightarrow {AB} = (2; - 2) \hfill \\ \overrightarrow {BC} = (2;2) \hfill \\ \overrightarrow {CA} = ( - 4;0) \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} AB = \sqrt {{2^2} + {{( - 2)}^2}} = 2\sqrt 2 \hfill \\ BC = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \hfill \\ CA = \sqrt {{{( - 4)}^2} + {0^2}} = 4 \hfill \\ \end{gathered} \right.\)
Chu vi của tam giác ABC là P = AB + BC + CA = \(4 + 4\sqrt 2 \)
Vậy chọn đáp án B.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-1, 1); B (1; 3) và C(1; -1). Khẳng định nào sau đây là đúng ?
Ta có:
\(\overrightarrow {AB} = (2;2),\overrightarrow {BC} = (0; - 4),\overrightarrow {AC} = (2; - 2)\)
\(\begin{gathered} \Rightarrow \left\{ \begin{gathered} AB = AC = 2\sqrt 2 \hfill \\ A{B^2} + A{C^2} = B{C^2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} \)
Do đó tam giác ABC là tam giác vuông cân tại A.
Vậy chọn đáp án D.
Cho tam giác ABC có a = 6 cm, b = 7 cm, c = 10 cm. Tam giác ABC là
Ta có:
\(\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{{6^2} + {7^2} - {{10}^2}}}{{2.6.7}} < 0 \Rightarrow C > {90^o}\)
Suy ta tam giác ABC là tam giác tù.
Vậy chọn đán án B.
Cho tam giác ABC có a = 4, b = 6, mc=4. Giá trị của c là
Ta có:
\(\begin{gathered} {m_c}^2 = \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4} \hfill \\ \Rightarrow \frac{{{c^2}}}{4} = \frac{{{a^2} + {b^2}}}{2} - {m_c}^2 = \frac{{{4^2} + {6^2}}}{2} - {4^2} = 10 \hfill \\ \Rightarrow {c^2} = 40 \Rightarrow c = 2\sqrt {10} \hfill \\ \end{gathered} \)
Vậy chọn đáp án A.
Cho tam giác ABC có a = BC, b = CA, c = AB, a + b = 2c. Khẳng định nào sau đây đúng?
Theo định lí sin trong tam giác ta có:
\(\frac{a}{{\sin A}} = 2R \Rightarrow a = 2R\sin A\)
Tương tự ta có b = 2RsinB, c = 2RsinC.
Ta có a+ b = 2c.
⇒ 2RsinA + 2RsinB = 2RsinC.
⇒ sin A + sin B = 2 sin C
Vậy chọn đáp án C.
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(-3; 0); B(3; 0) và C(2; 6). Gọi H(a; b) là tọa độ trực tâm của tam giác đã cho. Tính a + 6b
Ta có:
\(\left\{ \begin{gathered} \overrightarrow {AH} = \left( {a + 3;b} \right);\overrightarrow {BC} = \left( { - 1;6} \right) \hfill \\ \overrightarrow {BH} = \left( {a - 3;b} \right);\overrightarrow {AC} = \left( {5;6} \right) \hfill \\ \end{gathered} \right.\)
H là trực tâm tam giác ABC nên:
\(\left\{ \begin{gathered} \overrightarrow {AH} .\overrightarrow {BC} = 0 \hfill \\ \overrightarrow {BH} .\overrightarrow {AC} = 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} (a + 3).( - 1) + b.6 = 0 \hfill \\ (a - 3).5 + b.6 = 0 \hfill \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} a = 2 \hfill \\ b = \frac{5}{6} \hfill \\ \end{gathered} \right.\)
Suy ra a + 6b = 7
Vậy chọn đáp án C.

