Cho tam giác ABC và điểm M thỏa mãn \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \). Khi đó điểm M là:
A. Trọng tâm tam giác ABC
B. Trung điểm của AB
C. Đỉnh thứ tư của hình bình hành ACBM
D. Trung điểm của CI (I là trung điểm của AB)
Lời giải của giáo viên
 ToanVN.com
ToanVN.com
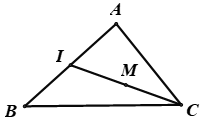
Gọi I là trung điểm AB.
Khi đó với mọi M ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
\(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow 2\overrightarrow {MI} + 2\overrightarrow {MC} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {MI} + \overrightarrow {MC} = \overrightarrow 0 \)
⇒ M là trung điểm của CI.
Vậy chọn đáp án D.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho ba điểm M(2; 2), N( - 4; - 4), P(5; 5). Khẳng định nào sau đây đúng?
Cho biết \(\sin \frac{\alpha }{3} = \frac{3}{5}\). Giá trị của \(P = 3{\sin ^2}\frac{\alpha }{3} + 5{\cos ^2}\frac{\alpha }{3}\) bằng bao nhiêu?
Cho hình vuông ABCD cạnh a, tâm O. Tính \(\left| {\overrightarrow {OA} + \overrightarrow {OC} } \right|\)?
Cho tam giác ABC. Vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) có giá chứa đường thẳng nào sau đây?
Cho hình vuông ABCD cạnh a. Giá trị của \(\overrightarrow {AB} .\overrightarrow {AC} \) là
Cho ngũ giác đều ABCDE, tâm O. Mệnh đề nào sau đây sai?
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow a = (1; - 3),\overrightarrow b = (6,x)\). Hai vectơ đó vuông góc với nhau khi và chỉ khi
Cho ba điểm A, B, C phân biệt sao cho \(\overrightarrow {AB} = k\overrightarrow {AC} \). Biết rằng B nằm giữa A và C. Giá trị k thỏa mãn điều kiện nào sau đây?
Cho hình bình hành ABCD. Tập hợp tất cả các điểm M thỏa mãn đẳng thức \(\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {MD} \) là
Tính giá trị biểu thức P = sin30°cos15° + sin150°cos165°.
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. Khi đó ABCD là hình bình hành nếu
Cho ba vectơ \(\overrightarrow a = \left( {2;1} \right),\overrightarrow b = \left( {3;4} \right),\overrightarrow c = \left( {7;2} \right)\). Giá trị của k, h để \(\overrightarrow c = k.\overrightarrow a + h.\overrightarrow b \) là
Cho tam giác đều ABC với đường cao AH. Đẳng thức nào sau đây đúng?
Cho các vectơ \(\overrightarrow a = ( - 1;2),\overrightarrow b = (3;5)\). Tìm các số thực x, y sao cho \(x\overrightarrow a + y\overrightarrow b = \overrightarrow 0 \)
Cho tam giác ABC với AB = c, BC = a, CA = b. Gọi CM là đường phân giác trong của góc C (M∈AB). Biểu thị nào sau đây là đúng?

