Các biểu thức đại số là :

\( 4x - 3;{x^2} - 5x + 1;{x^4} - 7y + z - 11\)

Hai số nguyên chẵn liên liếp là 2n và 2n+2 (với nn là số nguyên)

Tích các lập phương của hai số nguyên chẵn liên tiếp” được biểu thị bởi

\( {\left( {2n} \right)^3} . {\left( {2n + 2} \right)^3},n \in Z\)

Hai số nguyên lẻ liên liếp là 2n+1 và 2n+3 (với n là số nguyên)

“Tổng các bình phương của hai số nguyên lẻ liên tiếp” được biểu thị bởi

\( {\left( {2n + 1} \right)^2}+{\left( {2n + 3} \right)^2}\left( {n \in Z} \right)\)

Lượng nước chảy vào bể trong a phút là \(a.x(l)\)

Lượng nước chảy ra trong a phút \( \frac{1}{2}ax (l)\)

Vì ban đầu bể đang chứa 120lít nước nên lượng nước có trong bể sau a phút là: \( 120 + ax - \frac{1}{2}ax = 120 + \frac{1}{2}ax(l)\)

Với số nguyên n thì ba số n;n+1;n+2 là ba số nguyên liên tiếp. 

Biểu thức \( n.\left( {n + 1} \right).\left( {n + 2} \right)\) với n là số nguyên, được phát biểu là tích của ba số nguyên liên tiếp .

Giả sử độ dài cạnh huyền của tam giác vuông là c(c>0)

Áp dụng định lí Pytago vào tam giác vuông có hai cạnh góc vuông là a và b ta có: \(c^2=a^2+b^2\)

Vậy biểu thức tính bình phương cạnh huyền của một tam giác vuông có hai cạnh góc vuông là a và b là 

\(a^2+b^2.\)

Đáp án cần chọn là: B

Dấu hiệu là số con trong mỗi gia đình của một khu vực dân cư

Dấu hiệu điều tra là: Trình độ văn hóa của mỗi công nhân

Thay \(x=0,5 \text { và } y=1\) vào biểu thức \(G=0,25 x y^{2}-3 x^{2} y-5 x y-x y^{2}+x^{2} y+0,5 x y\) ta có 

\(G=0,25(0,5)-3(0,5)^{2}-5(0,5)-(0,5)+(0,5)^{2}+0,5(0,5)=-\frac{25}{8}\)

Thay \(x=-1 ; y=3\) vào biểu thức 

\(F=x^{2} y^{2}+x y+x^{3}+y^{3}+1\) ta có

\(F=(-1)^{2} 3^{2}+(-1) \cdot 3+(-1)^{3}+3^{3}+1=33\)

Thay \(x=\frac{1}{2} ; y=-\frac{1}{3}\) vào biểu thức \(E=3 x^{2} y+6 x^{2} y^{2}+3 x y^{3}\) ta có

\(E=3\left(\frac{1}{2}\right)^{2} \cdot\left(-\frac{1}{3}\right)+6\left(\frac{1}{2}\right)^{2} \cdot\left(-\frac{1}{3}\right)^{2}+3\left(\frac{1}{2}\right)\left(-\frac{1}{3}\right)^{3}=-\frac{5}{36}\)

Thay \(a=-\frac{1}{3} ; b=-\frac{1}{6}\) vào biểu thức \(D=12 a b^{2}\) ta có

\(D=12 \cdot\left(-\frac{1}{3}\right) \cdot\left(-\frac{1}{6}\right)^{2}=-\frac{1}{9}\)

Thay \(x=-\frac{1}{2} ; y=\frac{2}{3}\) vào biểu thức \(C=2 x^{2}+3 x y+y^{2}\) ta có

\(C=2\left(-\frac{1}{2}\right)^{2}+3\left(-\frac{1}{2}\right) \cdot\left(\frac{2}{3}\right)+\left(\frac{2}{3}\right)^{2}=-\frac{1}{18}\)

Thay \(a=-2 ; b=-\frac{1}{3}\) vào biểu thức \(B=\frac{1}{2} a^{2}-3 b^{2}\) ta có

\(B=\frac{1}{2}(-2)^{2}-3\left(-\frac{1}{3}\right)^{2}=\frac{5}{3}\)

Dấu hiệu ở đây là: Số điểm đạt được sau mỗi lần bắn cung của một xạ thủ.

Có 30 học sinh tham gia kiểm tra.

Ta có \(A B C=-\frac{3}{4} x^{5} y^{4} \cdot x y^{2} \cdot\left(-\frac{8}{9} x^{2} y^{5}\right)=\frac{2}{3} x^{8} y^{11}\)

Ta có \(A B=x^{3}\left(-\frac{5}{4} x^{2} y\right) \cdot \frac{2}{5} x^{3} y^{4}=-\frac{1}{2} x^{8} y^{5}\)

Hệ số của A.B là \(-\frac{1}{2}\)

Ta có \(A B=x^{3}\left(-\frac{5}{4} x^{2} y\right) \cdot \frac{2}{5} x^{3} y^{4}=-\frac{1}{2} x^{8} y^{5}\)

Ta có \(A B=\frac{1}{3} x y^{2} \cdot\left(-\frac{3}{4} y z\right)=-\frac{1}{4} x y^{3} z\)

 \(\begin{aligned} &A B=-2 x y^{2} z \cdot \frac{3}{4} x^{2} y z^{3}=\frac{-3}{2} x^{3} y^{3} z^{4}\\ &\text { Hệ số: } \frac{-3}{2} . \text { Biến: } x^{3} y^{3} z^{4} \end{aligned}\)

Ta có \(A B=-2 x y^{2} z \cdot \frac{3}{4} x^{2} y z^{3}=\frac{-3}{2} x^{3} y^{3} z^{4}\)

Các đơn thức đồng dạng:

Nhóm 1: \( - \frac{2}{3}{x^3}y;2{x^3}y\)

Nhóm 2: \(5{x^2}y;\frac{1}{2}{x^2}y\)

Nhóm 3: \( - x{y^2};6x{y^2}\)

Chọn đáp án B

Ta có:

N = 1000x²⁰²⁰y²⁰²¹ + 2000x²⁰²⁰y²⁰²¹

=(1000 + 2000)x²⁰²⁰y²⁰²¹ = 3000x²⁰²⁰y²⁰²¹

Thay x = 1 và y = 1 vào N ta được

N = 3000.1²⁰²⁰.1²⁰²¹ = 3000

Chọn đáp án C

Tích hai đơn thức \(\frac{1}{3}xyz\) và 2xy³z² với đơn thức 2x²y⁴z³ là

\(\frac{1}{2}xyz.2x{y^3}{z^2} = \left( {\frac{1}{2}.2} \right).\left( {x.x} \right)\left( {y.{y^3}} \right).\left( {z.{z^2}} \right) = {x^2}{y^4}{z^3}\)

Tổng cần tìm là:

x²y⁴z³ + 2x²y⁴z³ = (1 + 2)x²y⁴z³ = 3x²y⁴z³

Chọn đáp án B

Ta có:

2x²y²xy + (-5x³y³) = 2(x².x).(y².y) + (-5x³y³)

2x³y³ + (-5x³y³) = (2 + (-5))x³y³ = -3x³y³

Chọn đáp án D

Ta có : -3x² - 0,5x² + 2,5x² = (-3 - 0,5 + 2,5)² = -x²

Chọn đáp án C

Ta có 4x3y - (-2x³y) = 4x³y + 2x³y = 6x³y

Chọn đáp án B

 Vì trong một tam giác tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại và hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại nên các đáp án A, B, C đều đúng, đáp án D sai.

Từ D kẻ đường thẳng vuông góc với BC cắt BC tại E

Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:

BD cạnh huyền chung

 (BD là tia phân giác của góc B)

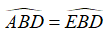
Khi đó: ΔABD = ΔEBD (cạnh huyền góc nhọn)

Suy ra: AD = DE (hai cạnh tương ứng) (1)

Lại có tam giác DEC vuông tại E có DC là cạnh huyền

Suy ra DC > DE (trong tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất) (2)

Từ (1) và (2) suy ra DC > AD hay AD < DC

Vậy A đúng, B, C, D sai.

Chọn đáp án A

Từ đề bài \(\hat C > \hat B ⇒AB>AC\).Trên cạnh AB lấy điểm E sao cho AC=AE.

Xét tam giác ACD và tam giác AED có: AC=AE

\( \widehat {CAD} = \widehat {DAB}\) (tính chất tia phân giác)

+ Cạnh AD chung

Suy ra: \(\Delta ACD=\Delta AED (c-g-c) \to DE=CD(1)\)

Và: \( \widehat {AED} = \widehat {ACD}\)

Mà \(\widehat {ACD}\) là góc nhọn nên \( \widehat {AED}\) là góc nhọn, suy ra \( \widehat {BED}=180^0- \widehat {AED}\) là góc tù, do đó: \( \widehat {BED}> \widehat {EBD}\)

Xét tam giác BED có: \( \widehat {BED}> \widehat {EBD}\) suy ra BD>DE (2)

Từ (1), (2): suy ra DC<BD

Xét ΔABC có: \( \widehat A + \widehat B + \widehat C = {180^0}\)

Ta có: \(\left\{ \begin{array}{l} \widehat B + \widehat C = {100^0}\\ \widehat B - \widehat C = {20^0} \end{array} \right. \to \left\{ \begin{array}{l} \widehat B = {60^0}\\ \widehat C = {40^0} \end{array} \right.\)

\( \widehat C < \widehat B < \widehat A=>AB<AC<BC\)

Xét ΔABC có:

\(\left\{ \begin{array}{l} AB + AC = 10cm(1)\\ AC - AB = 4cm(2) \end{array} \right. \to AC = 10 - AB\)

Thế vào (2) ta được:

\( 10 - AB - AB = 4 \Rightarrow 2AB = 6 \Rightarrow AB = 3{\mkern 1mu} cm.\)

\( \Rightarrow AC > AB \Rightarrow \widehat B > \widehat C\)

Vì trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn mà cạnh 9cm là cạnh nhỏ nhất trong tam giác nên góc nhỏ nhất là góc đối diện với cạnh có độ dài 9cm.

Vì A nằm trong góc xOy và cách đều hai tia Ox và Oy nên A nằm trên tia phân giác của góc xOy hay OA là tia phân giác của góc xOy

\(= > \widehat {NOA} = \widehat {MON} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}{.90^0} = {45^0}\)

Tam giác MOA vuông tại M có \(\widehat {MON} = {45^0}\)

Suy ra tam giác MAO vuông cân tại M nên MO = MA = 4 cm

Chứng minh tương tự ta cũng có NOA vuông cân tại N nên NO = NA = 4 cm

Vậy OM = ON = 4 cm.

Chọn đáp án C

Điểm A nằm trong góc xOy và cách đều hai tia Ox và Oy, do đó A nằm trên tia phân giác của góc xOy hay OA là tia phân giác của góc xOy

\(= > \widehat {xOA} = \frac{1}{2}\widehat {xOy} = \frac{1}{2}{.60^0} = {30^0}\)

Gọi D và E lần lượt là chân đường vuông góc của A lên Ox và Oy

Khi đó AD = AE = 6 cm; \(\widehat {DOA} = {30^0}\)

Trong tam giác AOD vuông ở D có \(\widehat {DOA} = {30^0}\)

Suy ra AD = 1/2 OA (Trong tam giác vuông cạnh đối diện với góc 30° bằng một nửa cạnh huyền).

Vậy OA = 2AD = 2.6 = 12cm.

Chọn đáp án D

Điểm E nằm trên tia phân giác góc A của tam giác ABC thì điểm E cách đều hai cạnh AB, AC

Chọn đáp án B

Ta có: D, E, O thuộc trung tuyến AM

Mà AD = DE = EM; O là trung điểm của DE

Nên AD = 1/3 AM; AE = 2/3 AM;

O là trung điểm của AM

Khi đó E là trọng tâm của tam giác ABC

(khoảng cách từ đỉnh tới trọng tâm của tam giác bằng 2/3 độ dài đường trung tuyến kẻ từ đỉnh đó).

Chọn đáp án B

M là trung điểm của BC nên AM là đường trung tuyến kẻ từ A của tam giác ABC

Mà G là trọng tâm của tam giác ABC

Do đó:

\(AG = \frac{2}{3}AM = > AM = \frac{3}{2}AG = \frac{3}{2}.12 = 18cm\)

Vậy AM = 18 cm.

Chọn đáp án A

Vì G là trọng tâm của tam giác ABC và AM là đường trung tuyến nên AG = (2/3)AM (tính chất ba đường trung tuyến của tam giác)

Do đó: AG = (2/3).9 = 6cm

Chọn đáp án C.