Đề thi giữa HK1 môn Toán 7 năm 2020 - Trường THCS Trường Thọ
-
Hocon247
-
30 câu hỏi
-
60 phút
-
56 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Cho các phân số sau: \(\frac{1}{2};\frac{{12}}{{28}};\frac{6}{{21}};\frac{{ - 30}}{{ - 70}};\frac{{15}}{{ - 35}};\frac{7}{3};\frac{{ - 3}}{7}\)
Có bao nhiêu phân số biểu diễn số hữu tỉ \(\frac37\)?
\(\begin{array}{l} \frac{1}{2} \ne \frac{3}{7}\\ \frac{{12}}{{28}} = \frac{{12:4}}{{28:4}} = \frac{3}{7}\\ \frac{6}{{21}} = \frac{{6:3}}{{21:3}} = \frac{2}{7} \ne \frac{3}{7}\\ \frac{{ - 30}}{{ - 70}} = \frac{{ - 30:( - 10)}}{{ - 70:( - 10)}} = \frac{3}{7}\\ \frac{{15}}{{ - 35}} = \frac{{15:5}}{{ - 35:5}} = \frac{3}{{ - 7}} \ne \frac{3}{7}\\ \frac{7}{3} \ne \frac{3}{7}\\ \frac{{ - 3}}{7} \ne \frac{3}{7} \end{array}\)
Vậy chọn đáp án B.
Trong các số hữu tỉ dưới đây, số nào lớn hơn \(\frac{{ - 2345}}{{2341}}\)?
A. Sai vì \(\frac{{ - 2346}}{{2341}} < \frac{{ - 2345}}{{2341}}\)
B. Sai vì \(\frac{{ - 4690}}{{4682}} = \frac{{ - 2345.2}}{{2341.2}} = \frac{{ - 2345}}{{2341}}\)
C. Sai vì \(\frac{{469}}{{ - 468}} = \frac{{469.( - 5)}}{{ - 468.( - 5)}} = \frac{{ - 2345}}{{2340}} < \frac{{ - 2345}}{{2341}}\)
D. Ta có:
\(\begin{array}{l} 497 > - 499 \Rightarrow \frac{{497}}{{ - 499}} > - 1\\ - 2345 < 2341 \Rightarrow \frac{{ - 2345}}{{2341}} < - 1\\ \Rightarrow \frac{{497}}{{ - 499}} > \frac{{ - 2345}}{{2341}} \end{array}\)
Vậy chọn đáp án D.
Có bao nhiêu khẳng định đúng trong các khẳng định sau đây?
(1) Số \(\frac{{11}}{{12}}\) là số hữu tỉ dương
(2) Số \(\frac{{12}}{{11}}\) là số hữu tỉ âm
(3) Số \(- \frac{{12}}{{11}}\) là số hữu tỉ dương
(4) Số \(-\frac{{11}}{{12}}\) là số hữu tỉ âm
(5) Số \(\frac{0}{{2020}}\) là số hữu tỉ dương
(1) Số \(\frac{{11}}{{12}}\) là số hữu tỉ dương → Đúng vì \(\frac{{11}}{{12}}>0\)
(2) Số \(\frac{{12}}{{11}}\) là số hữu tỉ âm → Sai vì \(\frac{{12}}{{11}}>0\)
(3) Số \(- \frac{{12}}{{11}}\) là số hữu tỉ dương → Sai vì \(- \frac{{12}}{{11}}<0\)
(4) Số \(-\frac{{11}}{{12}}\) là số hữu tỉ âm → Đúng vì \(-\frac{{11}}{{12}}<0\)
(5) Số \(\frac{0}{{2020}}\) là số hữu tỉ dương → Sai vì \(\frac{0}{{2020}}=0\)
Vậy chọn đáp án A.
Cho \(x + \frac{1}{2} = \frac{3}{4}\). Giá trị của x bằng
\(\begin{array}{l} x + \frac{1}{2} = \frac{3}{4}\\ x = \frac{3}{4} - \frac{1}{2}\\ x = \frac{3}{4} - \frac{2}{4}\\ x = \frac{1}{4} \end{array}\)
Vậy chọn đáp án D.
Gọi x0 là giá trị thỏa mãn \(\frac{5}{7}:x - \frac{2}{5} = \frac{1}{3}\). Chọn câu đúng?
\(\begin{array}{l} \frac{5}{7}:x - \frac{2}{5} = \frac{1}{3}\\ \frac{5}{7}:x = \frac{1}{3} + \frac{2}{5}\\ \frac{5}{7}:x = \frac{{11}}{{15}}\\ x = \frac{5}{7}:\frac{{11}}{{15}}\\ x = \frac{5}{7}.\frac{{15}}{{11}}\\ x = \frac{{75}}{{77}} \end{array}\)
Vì 75 < 77 nên \(\frac{75}{77}<1\)
Vậy chọn đáp án A.
Cho biểu thức \(A = \left| {x + 2,3} \right| - \left| { - 1,5} \right|\). Khi x = -1 thì giá trị của A là
Thay x = -1 vào A ta được:
\(A = \left| { - 1 + 2,3} \right| - \left| { - 1,5} \right| = |1,3| - \left| { - 1,5} \right| = 1,3 - 1,5 = - 0,2\)
Vậy chọn đáp án B.
Số 12502020202 có tận cùng là chữ số
Vì số 1250 có chữ số tận cùng là 0 nên nâng lên lũy thừa nào khác 0 cũng có tận cùng là 0
Do đó 12502020202 có tận cùng là chữ số 0
Vậy chọn đáp án A.
Viết biểu thức \({3^4}{.3^5}:\frac{1}{{27}}\) dưới dạng lũy thừa của một số ta được:
\({3^4}{.3^5}:\frac{1}{{27}} = {3^{4 + 5}}:\frac{1}{{{3^3}}} = {3^9}{.3^3} = {3^{9 + 3}} = {3^{12}}\)
Vậy chọn đáp án C.
Cho bốn số m, n, 5, 7 với m, n ≠ 0 và 5m = 7n, một tỉ lệ thức đúng được thiết lập từ bốn số trên là?
Từ đẳng thức: 5m = 7n, ta có tỉ lệ thức \(\frac{5}{7} = \frac{n}{m}\)
Vậy chọn đáp án D.
Giá trị của x thỏa mãn đẳng thức: \(\frac{{{x^2}}}{6} = \frac{{24}}{{25}}\)
\(\begin{array}{l} \frac{{{x^2}}}{6} = \frac{{24}}{{25}}\\ \Rightarrow 25{x^2} = 24.6\\ \Rightarrow {x^2} = \frac{{24.6}}{{25}} = \frac{{144}}{{25}}\\ \Rightarrow x = \pm \frac{{12}}{5} \end{array}\)
Vậy chọn đáp án A.
Biết \(\frac{x}{y} = \frac{7}{8}\) và x + y = 90. Hai số x, y lần lượt là?
Ta có:
\(\begin{array}{l} \frac{x}{y} = \frac{7}{8}\\ \Rightarrow \frac{x}{7} = \frac{y}{8} \end{array}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
\(\begin{array}{l} \frac{x}{7} = \frac{y}{8} = \frac{{x + y}}{{7 + 8}} = \frac{{90}}{{15}} = 6\\ \Rightarrow \left\{ \begin{array}{l} \frac{x}{7} = 6\\ \frac{y}{8} = 6 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 7.6 = 42\\ y = 8.6 = 48 \end{array} \right. \end{array}\)
Vậy chọn đáp án B
Viết số thập phân 0,16 dưới dạng phân số tối giản là
\(0,16 = \frac{{16}}{{100}} = \frac{{16:4}}{{100:4}} = \frac{4}{{25}}\)
Vậy chọn đáp án A.
Kết quả làm tròn số 0, 7126 đến chữ số thập phân thứ ba là
Vì 6 > 5 nên 0, 7126 ≈ 0,713
Vậy chọn đáp án B.
\(\sqrt {196} \) bằng:
\(\sqrt{196}=14\)
Vậy chọn đáp án D.
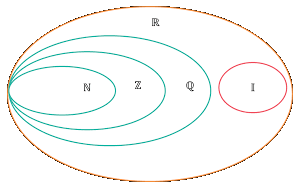
Chọn câu đúng
Dựa vào bểu đồ ven dưới đây suy ra chỉ có câu A đúng.
Vậy chọn đáp án A.
Cho hàm số y = f (x) = 2x2 + 3. Ta có:
y = f (x) = 2x2 + 3
Với x = 0 ⇒ f(0) = 2.02 + 3 = 3
Với x = 1 ⇒ f(1) = 2.12 + 3 = 5
Với x = -1 ⇒ f(-1) = 2.(-1)2 + 3 = 5
Với x = -2 ⇒ f(-2) = 2.(-2)2 + 3 = 11
Vậy chọn đáp án D.
Một điểm bất kì trên trục hoành có tung độ bằng:
Điểm thuộc trục hoành sẽ có trung độ bằng 0.
Vậy chọn đáp án B.
Đồ thị hàm số y = ax (a ≠ 0) là:
Đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ.
Vậy chọn đáp án C.
Góc \(\widehat {xOy}\) đối đỉnh với góc \(\widehat {x'Oy'}\) khi:

Dựa vào hình vẽ ta thấy cả ba câu đều đúng,
Vậy chọn đáp án D.
Chọn câu trả lời đúng nhất. Nếu đường thẳng xy là đường trung trực của đoạn thẳng AB thì:
Dựa vào định nghĩa đường trung trực ta chọn đáp án A.
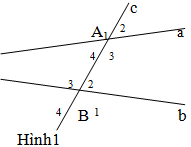
Đáp án nào sau đây không đúng? Trong hình 1, các cặp góc đồng vị là:
Chọn đáp án D vì Góc A3 và góc B3 là hai góc so le trong.
Vẽ cặp góc so le trong xAB và yBA sao cho \(\widehat {xAB} = {56^0};\widehat {yBA} = {65^0}\). Ta có:

Vậy chọn đáp án B.
Dạng phát biểu khác của “Tiên đề Ơ-CLít” là:
Dựa vào “Tiên đề Ơ-CLít” → Chọn câu A.
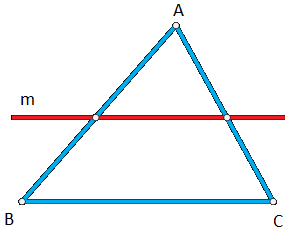
Cho tam giác ABC. Nếu đường thẳng m song song với cạnh BC và cắt cạnh AB, thì:
Dựa vào hình vẽ ta chọn đáp án A.
Chứng minh định lí là:
Chứng minh định lí là: Dùng lập luận để từ giả thiết suy ra kết luận.
Vậy chọn đáp án A.
Cho tam giác ABC. Ta có:
Tổng ba góc của một tam giác bằng 180o
Vậy chọn đáp án A.
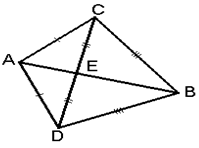
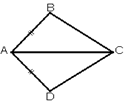
Cho hình vẽ dưới đây. Các tam giác bằng nhau theo trường hợp c- c-c là:
* Xét ∆ ABC và ∆ ABD có:
+ AB: cạnh chung
+ AC = AD
+ BC = BD
⇒ ∆ ABC = ∆ ABD
* Xét ∆ ACE và ∆ ADE có:
+ AE là cạnh chung
+ AC = AD
+ CE = DE
⇒ ∆ ACE = ∆ ADE
* Xét ∆ BCE và ∆ BDE có
+ BE là cạnh chung
+ BC = BD
+ CE = DE
⇒ ∆ BCE = ∆ BDE
Vậy chọn đáp án D.
Chọn câu trả lời đúng. Cho hình vẽ dưới đây.
Cần phải có thêm yếu tố nào để ∆ BAC = ∆ DAC (c- g-c)
Xét ∆ BAC và ∆ DAC có:
+ AC: cạnh chung
+ AB = AD
⇒ Phải có \(\widehat {BAC} =\widehat {DAC}\) thì ∆ BAC = ∆ DAC
Vậy chọn câu B.
Chọn câu trả lời đúng. Cho hình vẽ dưới đây.
Cần phải có thêm yếu tố nào để ∆ BAC = ∆ DAC (c- g-c)
Xét ∆ BAC và ∆ DAC có:
+ AC: cạnh chung
+ AB = AD
⇒ Phải có \(\widehat {BAC} =\widehat {DAC}\) thì ∆ BAC = ∆ DAC
Vậy chọn câu B.
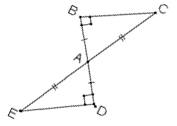
Cho hình vẽ dưới đây.
Hãy chọn câu sai:
Vì giả thiết không cho BC = DE nên ∆ ABC và ∆ ADE không thể bằng nhau theo trường hợp c.c.c.
Vậy chọn đáp án D.