Đề thi giữa HK1 môn Toán 7 năm 2020 - Trường THCS Ngô Sĩ Liên
-
Hocon247
-
30 câu hỏi
-
60 phút
-
48 lượt thi
-
Dễ
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Hình vẽ nào sau đây biểu diễn số hữu tỉ \(\frac34\) trên trục số?
Để biểu diễn số hữu tỉ \(\frac34\) trên trục số, ta làm như sau:
- Vẽ trục số
- Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 4 phần bằng nhau, lấy một đoạn làm đơn vị mới, ta được đơn vị mới bằng \(\frac14\) đơn vị cũ.
- Số hữu tỉ \(\frac34\) được biểu diễn bởi điểm K nằm về phía bên phải điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới như hình dưới đây:
.png)
Vậy chọn đáp án A.
Cho hai số hữu tỉ sau \(x = \frac{{25}}{{ - 35}} \ và \ y = \frac{{ - 444}}{{777}}\). Khẳng định nào sau đây là đúng?
Ta có:
\(\begin{array}{l} x = \frac{{25}}{{ - 35}} = \frac{{ - 25}}{{35}} = \frac{{ - 5.5}}{{5.7}} = \frac{{ - 5}}{7}\\ y = \frac{{ - 444}}{{777}} = \frac{{ - 4.111}}{{7.111}} = \frac{{ - 4}}{7} \end{array}\)
Vì \( - 5 < - 4 \Rightarrow \frac{{ - 5}}{7} < \frac{{ - 4}}{7} \Rightarrow \frac{{25}}{{ - 35}} < \frac{{ - 444}}{{777}}\)
Vậy chọn đáp án B.
Với giá trị nào dưới đây của m thì số hữu tỉ \(x = \frac{{m + 1}}{{2100}}\) là số hữu tỉ dương?
x là số hữu tỉ dương khi m + 1 > 0 (vì 2100 > 0)
⇒ m > -1
Vì trong 4 đáp án đã cho chỉ có 2 > - 1, nên B đúng.
Vậy chọn đáp án B.
Kết quả của phép tính \(\frac{3}{5} + \left( {\frac{{ - 5}}{6}} \right) + \left( {\frac{{ - 1}}{3}} \right)\) là:
\(\frac{3}{5} + \left( {\frac{{ - 5}}{6}} \right) + \left( {\frac{{ - 1}}{3}} \right) = \frac{3}{5} - \frac{5}{6} - \frac{2}{6} = \frac{3}{5} - \frac{7}{6} = \frac{{18}}{{30}} - \frac{{35}}{{30}} = - \frac{{17}}{{30}}\)
Vậy chọn đáp án C.
Kết quả của phép tính \(\left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right):\frac{4}{5} + \left( {\frac{{ - 1}}{3} + \frac{4}{7}} \right):\frac{4}{5}\)
\(\begin{array}{l} \left( {\frac{{ - 2}}{3} + \frac{3}{7}} \right):\frac{4}{5} + \left( {\frac{{ - 1}}{3} + \frac{4}{7}} \right):\frac{4}{5}\\ = \left( {\frac{{ - 14}}{{21}} + \frac{9}{{21}}} \right):\frac{4}{5} + \left( {\frac{{ - 7}}{{21}} + \frac{{12}}{{21}}} \right):\frac{4}{5}\\ = \frac{{ - 5}}{{21}}:\frac{4}{5} + \frac{5}{{21}}:\frac{4}{5}\\ = \frac{{ - 25}}{{84}} + \frac{{25}}{{84}}\\ = 0 \end{array}\)
Vậy chọn đáp án A.
Với mọi \(x \in Q\). Khẳng định nào dưới đây là sai?
Với mọi \(x \in Q\) ta luôn có |x| \(\ge\) x, |x| \(\ge\) 0, |x| = |-x|
Vậy chọn đáp án D.
Cho hai số a = 9920 và b = 999910. Khẳng định nào sau đây là đúng
Ta có:
a = 9920 = 992.10 = (992)10 = (99.99)10 = 980110
b = 999910
Vì 0 < 9801 < 9999
Suy ra 980110 < 999910 (hai lũy thừa cùng cơ số)
Do đó 9920 < 999910
Nên a < b
Vậy chọn đáp án B
Số 530 viết dưới dạng lũy thừa với số mũ bằng 15 là
Ta có: 530 = 52.15 = (52)15 = 2515
Vậy chọn đáp án C
Chọn câu đúng, nếu ab = cd với a, b, c, d ≠ 0 thì
Ta có: \(ab = cd \Rightarrow \frac{a}{c} = \frac{d}{b}\)
Vậy chọn đáp án B.
Cho tỉ lệ thức \(\frac{{2x}}{9} = \frac{a}{7}\) (với a là hằng số đã biết, a ≠ 0) thì
\(\frac{{2x}}{9} = \frac{a}{7} \Rightarrow 2x.7 = 9.a \Rightarrow 14x = 9a \Rightarrow x = \frac{{9a}}{{14}}\)
Vậy chọn đáp án B.
Cho 2x = 9y và y – x = 49. Tìm giá trị của x và y?
Ta có: \(2x = 9y \Rightarrow \frac{x}{9} = \frac{y}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l} \frac{x}{9} = \frac{y}{2} = \frac{{y - x}}{{2 - 9}} = \frac{{49}}{{ - 7}} = - 7\\ \Rightarrow \left\{ \begin{array}{l} \frac{x}{9} = - 7\\ \frac{y}{2} = - 7 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} x = 9.( - 7) = - 63\\ y = 2.( - 7) = - 14 \end{array} \right. \end{array}\)
Vậy chọn đáp án A.
So sánh hai số 0,53 và 0,( 53)
Ta có: 0,(53) = 0,53535353...
Suy ra 0,53 < 0,( 53)
Vajayc họn đáp án B.
Thực hiện phép tính 13 : 27 rồi làm tròn đến chữ số thập phân thứ hai được kết quả là:
Ta có: 13 : 27 = 0,481481481...
Vì 1 < 5 nên 0,481481481... ≈ 0,48
Vậy chọn đáp án C.
Chọn câu trả lời sai. Nếu \(\sqrt x = \frac{2}{3}\) thì x bằng:
A. Đúng vì \(\sqrt{{\left( {\frac{2}{3}} \right)^2}}=\frac23\)
B. Đúng vì \(\sqrt{{\left( {-\frac{2}{3}} \right)^2}}=\frac23\)
C. Đúng vì \(\sqrt{\frac49}=\frac23\)
D. Sai vì \(-{\left( { - \frac{2}{3}} \right)^2}=-\frac49<0\)
Vaajyc họn đáp án D.
Chọn chữ số thích hợp điền vào...:
- 5,07< - 5,... 4
- 5,07< - 5,... 4
⇒ - 5,07< - 5,04
Vậy chọn đáp án C.
Cho hàm số y = \(\sqrt x\) - 1 . Nếu y = 5 thì x bằng
y = \(\sqrt x\) - 1
Với y = 5 thì \(\sqrt x\) - 1 = 5
\(\sqrt x\) = 6
x = 36
Vậy họn đáp án B.
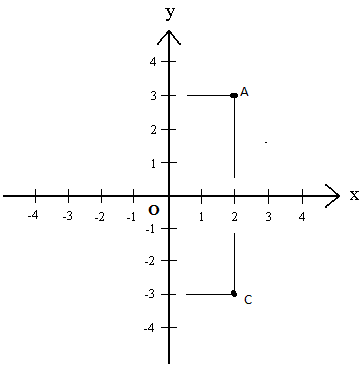
Hai điểm đối xứng qua trục hoành thì
Ta có hai điểm A và B đối xứng nhau qua trục hoành
Suy ra A và B có hoành độ bằng nhau, tung độ đối nhau.
Vậy chọn đáp án D
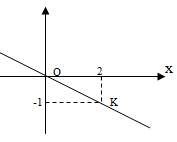
Cho hình vẽ dưới đây. Đường thẳng OK là đồ thị của hàm số:
Hàm số y =ax
Ta có K (2; -1) thuộc đồ thị hàm số
Nên thay x = 2, y = -1 vào y = ax ta được
-1 = a.2
a = -0,5
Vậy chọn đáp án
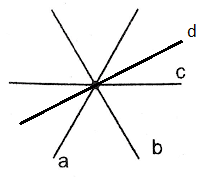
Chọn câu phát biểu đúng
Dựa vào các hình dưới đây sauy ra đáp án B và C sai
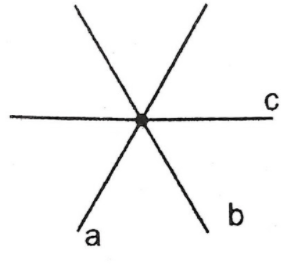
Vậy chọn đáp án A.
Chọn câu phát biểu đúng
A. Sai vì chúng có thể cắt nhau mà không vuông góc
B. Đúng
C và D Sai vì chúng tạo thành 4 góc vuông
Vậy chọn đáp án B.
Chọn câu trả lời sai:
Nếu một đường thẳng cắt hai đường thẳng, trong các góc tạo thành có một cặp góc so le trong bằng nhau. Khi đó
Nếu một đường thẳng cắt hai đường thẳng, trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.
→ Mỗi cặp góc đồng vị bằng nhau.
Vậy chọn đáp án B.
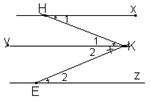
Cho hình vẽ dưới đây, biết \(\widehat {{H_1}} = \widehat {{K_1}}\) và \(\widehat {{K_2}} = \widehat {{E_2}}\).
Có các đường thẳng song song là
Ta có: \(\widehat {{H_1}} = \widehat {{K_1}}\) ⇒ Kx // Ky
\(\widehat {{K_2}} = \widehat {{E_2}}\) ⇒ Ky // Ez
Suy ra Kx // Ky // Ez
Vậy chọn đáp án D.
Cách phát biểu khác của “Tiên đề Ơ-CLít” là:
Dựa vào “Tiên đề Ơ-CLít” ta thấy cả ba phái biểu đều đúng.
Vậy chọn đáp án D.
Cho hình vẽ dưới đây, biết:
d \(\bot\) MQ, d \(\bot\) NP và \(\widehat {MQP} = {110^0}\).
Số đo x của góc NPQ bằng:
Ta có: d \(\bot\) MQ, d \(\bot\) NP
⇒ MQ // NP
⇒ \(\widehat {NPQ} +\widehat {MQP}= {180^0}\) (hai góc trong cùng phía)
⇒ \(\widehat {NPQ}= {180^0}- {110^0}= {80^0}\)
Vậy chọn đáp án C.
Xét tính đúng sai của các khẳng định dưới đây:
1. Hai góc đối đỉnh thì bằng nhau
2. Hai góc bằng nhau thì đối đỉnh
3. Nếu M là trung điểm của đoạn thẳng AB thì MA = MB
4. Nếu MA = MB thì M là trung điểm của AB
1. Hai góc đối đỉnh thì bằng nhau → đúng
2. Hai góc bằng nhau thì đối đỉnh → sai vì nó có thể là hai góc so le trong, hai góc đồng vị,...
3. Nếu M là trung điểm của đoạn thẳng AB thì MA = MB → đúng
4. Nếu MA = MB thì M là trung điểm của AB → sai vì có thể M không nằm trên đường thẳng AB.
Vậy chọn đáp án B.
Cho tam giác ABC vuông tại A. Ta có:
Ta có:
\(\widehat {A} + \widehat {B} + \widehat {C}=180^o\)
Mà \(\widehat {A} =90^o\) nên \( \widehat {B} + \widehat {C}=90^o\)
Vậy chọn đáp án D.
Trường hợp bằng nhau cạnh -cạnh -cạnh của hai tam giác là:
Trường hợp bằng nhau cạnh -cạnh -cạnh của hai tam giác là :
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau
Vậy chọn đáp án A.
Xét tính đúng sai của các câu sau:
1. Nếu hai cạnh và một góc của tam giác này bằng hai cạnh và một góc của tam giác kia thì hai tam giác đó bằng nhau
2. Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau
3. Nếu một cạnh góc vuông và một góc nhọn của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau
4. Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau
1. Sai vì góc đó phải xem giữa hai cạnh bằng nhau.
2. Đúng
3. Sai vì cạnh đó có thể không xem giữa hai góc bằng nhau
4. Đúng
Vậy chọn đáp án A.
Hai góc nhọn của tam giác vuông cân bằng
Mỗi góc nhọn của tam giác vuông cân bằng 45°
Vậy chọn đáp án B.
Cho tam giác MNP cân tại P có góc M = 60°. Khi đó
Ta có: tam giác MNP cân tại P có một góc M = 60°
Suy ra tam giác MNP đều (dấu hiệu nhận biết tam giác đều)
Vậy chọn đáp án C