Đề thi HK1 môn Toán 7 năm 2020 - Trường THCS Lê Hồng Phong
-
Hocon247
-
30 câu hỏi
-
60 phút
-
52 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Thực hiện phép tính: \(\dfrac{2}{3} + 0,75:\dfrac{3}{4} - 2\dfrac{1}{2}\)
Ta có:
\(\dfrac{2}{3} + 0,75:\dfrac{3}{4} - 2\dfrac{1}{2}\) \(\begin{array}{l} = \dfrac{2}{3} + \dfrac{3}{4}.\dfrac{4}{3} - \dfrac{5}{2}\\ = \dfrac{2}{3} + 1 - \dfrac{5}{2}\\ = \dfrac{4}{6} + \dfrac{6}{6} - \dfrac{{15}}{6}\\ = - \dfrac{5}{6}\end{array}\)
Chọn đáp án A
Thực hiện phép tính: \(5\sqrt {\dfrac{1}{{25}}} - \sqrt {\dfrac{1}{4}} .\sqrt 9\)
Ta có:
\(5\sqrt {\dfrac{1}{{25}}} - \sqrt {\dfrac{1}{4}} .\sqrt 9\)
\(\begin{array}{l} = 5.\dfrac{1}{5} - \dfrac{1}{2}.3\\ = 1 - \dfrac{3}{2}\\ = \dfrac{2}{2} - \dfrac{3}{2}\\ = - \dfrac{1}{2}\end{array}\)
Thực hiện phép tính: \(\dfrac{{{{10}^9}{{.49}^4}}}{{{{14}^8}{{.25}^5}}}\)
Ta có:
\(\dfrac{{{{10}^9}{{.49}^4}}}{{{{14}^8}{{.25}^5}}}\)
\(\begin{array}{l} = \dfrac{{{{\left( {2.5} \right)}^9}.{{\left( {{7^2}} \right)}^4}}}{{{{\left( {2.7} \right)}^8}.{{\left( {{5^2}} \right)}^5}}}\\ = \dfrac{{{2^9}{{.5}^9}{{.7}^8}}}{{{2^8}{{.7}^8}{{.5}^{10}}}}\\ = \dfrac{{2.1.1}}{{1.1.5}}\\ = \dfrac{2}{5}\end{array}\)
Tìm x, biết: \(\dfrac{1}{8} - \left( {x - \dfrac{1}{2}} \right) = \sqrt {\dfrac{1}{9}}\)
Ta có:
\(\dfrac{1}{8} - \left( {x - \dfrac{1}{2}} \right) = \sqrt {\dfrac{1}{9}}\)
\(\begin{array}{l}\dfrac{1}{8} - \left( {x - \dfrac{1}{2}} \right) = \dfrac{1}{3}\\x - \dfrac{1}{2} = \dfrac{1}{8} - \dfrac{1}{3} = - \dfrac{5}{{24}}\\x = - \dfrac{5}{{24}} + \dfrac{1}{2}\\x = \dfrac{7}{{24}}\end{array}\)
Tìm x, biết: \(\left| {\dfrac{5}{{18}} - x} \right| + \dfrac{1}{5} = \dfrac{1}{2}\)
Ta có:
\(\left| {\dfrac{5}{{18}} - x} \right| + \dfrac{1}{5} = \dfrac{1}{2}\)
\(\begin{array}{l}\left| {\dfrac{5}{{18}} - x} \right| = \dfrac{1}{2} - \dfrac{1}{5}\\\left| {\dfrac{5}{{18}} - x} \right| = \dfrac{3}{{10}}\end{array}\)
Một lớp học có 32 học sinh gồm ba loại học lực: giỏi, khá, trung bình. Biết số học sinh học lực giỏi, khá, trung bình tỉ lệ với 9:5:2. Hỏi lớp có bao nhiêu học sinh giỏi?
Gọi số học sinh giỏi, khá, trung bình lần lượt là x, y, z \((0 < x,y,z < 32,x,y,z \in \mathbb{N})\)
Theo bài ra ta có: \(\left\{ \begin{array}{l}x + y + z = 32\\\dfrac{x}{9} = \dfrac{y}{5} = \dfrac{z}{2}\end{array} \right.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{9} = \dfrac{y}{5} = \dfrac{z}{2}\) \( = \dfrac{{x + y + z}}{{9 + 5 + 2}} = \dfrac{{32}}{{16}} = 2\)
+) \(\dfrac{x}{9} = 2 \Rightarrow x = 2.9 = 18\)
+) \(\dfrac{y}{5} = 2 \Rightarrow y = 2.5 = 10\)
+) \(\dfrac{z}{2} = 2 \Rightarrow z = 2.2 = 4\)
Vậy lớp đó có 18 học sinh giỏi.
Bạn Lan dự định mua 25 quyển tập với giá tiền phải trả là 200.000 đồng. Khi đến cửa hàng thì Lan thấy tập tăng giá thêm 1000 đồng một quyển. Hỏi bạn Lan có thể mua nhiều nhất là bao nhiêu quyển tập?
Giá tiền một quyển tập bạn Lan phải trả theo dự định là: 200000:25 = 8000 đồng
Thực tế giá tiền mỗi quyển tập là: 8000 + 1000 = 9000 đồng
Ta có 200000:9000 = 22 dư 2000 đồng nên bạn Lan mua được nhiều nhất là 22 quyển tập.
Chọn đáp án D
Giá trị của hàm số \(y = f\left( x \right) = 3{x^2} + 2\) tại x = - 1 bằng bao nhiêu?
Thay x = - 1 vào hàm số \(y = f\left( x \right) = 3{x^2} + 2\) ta được:
\(f\left( { - 1} \right) = 3.{\left( { - 1} \right)^2} + 2 = 5\)
Chọn D
Cho \(\Delta ABC\) có góc A bằng \(70^\circ \), góc B bằng \(50^\circ \). Khi đó góc ngoài của \(\Delta ABC\) tại đỉnh C bằng bao nhiêu độ?
Góc ngoài của \(\Delta ABC\) tại đỉnh C bằng: \(\widehat A + \widehat B = {70^0} + {50^0} = {120^0}.\)
Chọn C
Điểm nào sau đây thuộc đồ thị hàm số y = 4x?
Thay \(x = \dfrac{1}{3};y = \dfrac{4}{3}\) vào hàm số y = 4x ta được:
\(\dfrac{4}{3} = 4.\dfrac{1}{3} \Leftrightarrow \dfrac{4}{3} = \dfrac{4}{3}\) (luôn đúng)
Nên điểm có tọa độ \(\left( {\dfrac{1}{3};\dfrac{4}{3}} \right)\) thuộc đồ thị hàm số y = 4x.
Chọn A
Cho \(\Delta ABC\) có góc B bằng góc C và góc A bằng \(80^\circ \). Khi đó số đo của góc B bằng bao nhiêu?
Xét tam giác ABC có: \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong tam giác)
Mà
\(\widehat B = \widehat C \Rightarrow 2\widehat B + \widehat A = {180^0}\) \( \Rightarrow 2\widehat B = {180^0} - {80^0} \Rightarrow 2\widehat B = {100^0}\) \( \Rightarrow \widehat B = {50^0}.\)
Chọn B
Thực hiện phép tính: \(\dfrac{5}{6} + \dfrac{2}{3} - 0,5\)
Ta có:
\(\dfrac{5}{6} + \dfrac{2}{3} - 0,5\)
\(\begin{array}{l} = \dfrac{5}{6} + \dfrac{2}{3} - \dfrac{1}{2}\\ = \dfrac{5}{6} + \dfrac{4}{6} - \dfrac{3}{6}\\ = \dfrac{{5 + 4 - 3}}{6}\\ = \dfrac{6}{6} = 1\end{array}\)
Thực hiện phép tính: \(\left( - \dfrac{3}{4} + \dfrac{2}{3} \right): \dfrac{5}{11} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
Ta có:
\(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
\(\begin{array}{l} = \left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right).\dfrac{{11}}{5} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - \dfrac{3}{4} + \dfrac{2}{3} - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left[ {\left( { - \dfrac{3}{4} - \dfrac{1}{4}} \right) + \left( {\dfrac{2}{3} + \dfrac{1}{3}} \right)} \right].\dfrac{{11}}{5}\\ = \left( { - 1 + 1} \right).\dfrac{{11}}{5}\\ = 0.\dfrac{{11}}{5}\\ = 0\end{array}\)
Thực hiện phép tính: \({\left( { - 2} \right)^2} + \left| { - \dfrac{3}{2}} \right|.\sqrt {36} - \dfrac{8}{3}.\sqrt 9 \)
Ta có:
\({\left( { - 2} \right)^2} + \left| { - \dfrac{3}{2}} \right|.\sqrt {36} - \dfrac{8}{3}.\sqrt 9 \)
\(\begin{array}{l} = 4 + \dfrac{3}{2}.6 - \dfrac{8}{3}.3\\ = 4 + 9 - 8\\ = 5\end{array}\)
Tìm x biết: \(0,2 + \dfrac{2}{3}x = \dfrac{1}{3}\)
Ta có:
\(0,2 + \dfrac{2}{3}x = \dfrac{1}{3}\)
\(\begin{array}{l}\dfrac{2}{3}x = \dfrac{1}{3} - 0,2\\\dfrac{2}{3}x = \dfrac{1}{3} - \dfrac{1}{5}\\\dfrac{2}{3}x = \dfrac{2}{{15}}\\x = \dfrac{2}{{15}}:\dfrac{2}{3}\\x = \dfrac{1}{5}\end{array}\)
Tìm x biết: \(\left| {2x - 1} \right| - \dfrac{1}{2} = \dfrac{1}{3}\)
Ta có:
\(\left| {2x - 1} \right| - \dfrac{1}{2} = \dfrac{1}{3}\)
\(\begin{array}{l}\left| {2x - 1} \right| = \dfrac{1}{3} + \dfrac{1}{2}\\\left| {2x - 1} \right| = \dfrac{5}{6}\end{array}\)
+) TH1: \(2x - 1 = \dfrac{5}{6}\)
\(\begin{array}{l}2x = \dfrac{5}{6} + 1\\2x = \dfrac{{11}}{6}\\x = \dfrac{{11}}{6}:2\\x = \dfrac{{11}}{{12}}\end{array}\)
+) TH2: \(2x - 1 = - \dfrac{5}{6}\)
\(\begin{array}{l}2x = - \dfrac{5}{6} + 1\\2x = \dfrac{1}{6}\\x = \dfrac{1}{6}:2\\x = \dfrac{1}{{12}}\end{array}\)
Vậy \(x = \dfrac{{11}}{{12}} \,\, hoặc \,\, x = \dfrac{1}{{12}}\)
Hai góc đối đỉnh thì
Hai góc đối đỉnh thì bằng nhau (tính chất hai góc đối đỉnh).
Chọn đáp án A.
Cho đường thẳng MN cắt đoạn thẳng AB tại I. Đường thẳng MN là trung trực của đoạn thẳng AB nếu:
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.
Vậy đường thẳng MN là trung trực của đoạn thẳng AB nếu MN ⊥ AB và I là trung điểm của AB (MN cắt AB tại I).
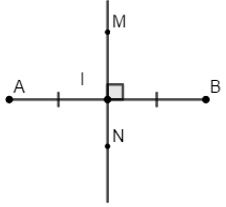
Chọn đáp án D.
Ba đường thẳng phân biệt cắt nhau tại O tạo thành bao nhiêu cặp góc đối đỉnh? (Không kể các góc bẹt).
Ba đường thẳng cắt nhau tại điểm O tạo thành 6 tia chung gốc.
Mỗi tia tạo với 5 tia còn lại là là 5 góc, mà có 6 tia, như vậy có tất cả số góc là: 5.6 = 30 góc
Vì mỗi góc được lặp lại hai lần nên 3 đường thẳng cắt nhau tạo thành: 30 : 2 = 15 góc
Ba đường thẳng cắt nhau tạo thành 3 góc bẹt. Vậy có tất cả số góc khác góc bẹt là: 15 - 3 = 12 góc
Có tất cả 12 góc khác góc bẹt mà mỗi góc lại có một góc đối đỉnh với nó nên ta có số cặp góc đối đỉnh là: 12 : 2 = 6 cặp
Chọn đáp án B.
Cho ba đường thẳng a, b, c phân biệt. Biết a // b và a // c, suy ra:
a, b, c là ba đường thẳng phân biệt
Ta có: \(\left. \begin{array}{l} a//b\\ a//c \end{array} \right\}\) ⇒ b // c (tính chất ba đường thẳng song song).
Chọn đáp án A.
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị:
Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau.
Chọn đáp án B.
Số đường thẳng song song với đường thẳng a cho trước là:
Cho trước một đường thẳng a thì có vô số đường thẳng song song với a.

Chọn đáp án D.
Hai đường thẳng xx' và yy' cắt nhau tại O, trong đó \(\widehat {xOy}\) = 70o thì số đo góc x'Oy' là:
.png)
Góc xOy và x'Oy' là hai góc đối đỉnh nên \(\widehat {x'Oy}' = \widehat {xOy}\) = 70o.
Chọn đáp án A.
Hai đường thẳng song song là hai đường thẳng:
Hai đường thẳng song song là hai đường thẳng không có điểm chung.
Chọn đáp án B.
Chứng minh định lí là:
Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận.
Chọn đáp án A.
Xem hình vẽ, biết MN = 4 cm. Số đo của đoạn thẳng MC?
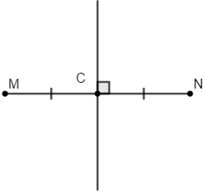
.png)
Theo hình vẽ ta thấy C là trung điểm của MN
Nên MC = \(\frac{1}{2}\) MN = \(\frac{1}{2}\).4 = 2 cm.
Chọn đáp án D.
Khoanh tròn vào phát biểu sai:
Cho ba điểm M, N, P không thẳng hàng
.png)
Theo tiên đề Ơ-clít, qua M có duy nhất một đường thẳng song song với NP nên A đúng.
Qua M kẻ được một và chỉ một đường thẳng vuông góc với đường thẳng NP (tính chất thừa nhận hai đường thẳng vuông góc) nên B đúng.
Vậy cả A và B đều đúng.
Do đó câu C sai.
Chọn đáp án C.
Cho góc xOy = 20o thì góc đối đỉnh với góc xOy có số đo là:
Hai góc đối đỉnh thì bằng nhau nên góc đối đỉnh với góc xOy bằng 20o.
Chọn đáp án A
Chọn khẳng định sai:
+) Nếu một đường thẳng cắt hai đường thẳng song song thì trong các góc tạo thành có
- Hai góc trong cùng phía bù nhau
- Hai góc so le trong bằng nhau
+) Hai đường thẳng song song thì cắt nhau.
+) Hai góc bằng nhau chưa chắc đã đối đỉnh vì có thể chúng không chung gốc như hình vẽ sau:
.png)
Vậy đáp án A, B, C đúng và D sai.
Chọn đáp án D
Cho hình vẽ: a // b, A1 = 60o, số đo góc B3 là:
.png)
Theo tiên đề Ơ-c lít: Qua một điểm nằm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Chọn đáp án D.

