Đề thi giữa HK2 môn Toán 7 năm 2021-2022 - Trường THCS Tô Hiến Thành
-
Hocon247
-
40 câu hỏi
-
60 phút
-
44 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Bậc của đa thức \(A = {y^9} + 3{{\rm{x}}^3}y + 2x{y^2} - 3{x^3}y - {y^9} + xy\) là:
\(\begin{array}{l}A = {y^9} + 3{{\rm{x}}^3}y + 2x{y^2} - 3{x^3}y - {y^9} + xy\\ = {y^9} - {y^9} + 3{{\rm{x}}^3}y - 3{{\rm{x}}^3}y + 2x{y^2} + xy\\ = 2x{y^2} + xy\end{array}\)
Vậy bậc của đa thức A là \( 1+2=3\).
Chọn D.
Một tam giác cân có độ dài hai cạnh là \(7{\mkern 1mu} cm\) và \(3{\mkern 1mu} cm\). Khi đó chu vi tam giác đó là:
Áp dụng bất đẳng thức tam giác ta có: \(7 - 3 < 7 < 7 + 3 \Rightarrow \) độ dài ba cạnh của tam giác đó là: \(7cm,{\mkern 1mu} 7cm,{\mkern 1mu} 3cm.\) Chu vi của tam giác đó là: \(7 + 7 + 3 = 17cm.\)
Chọn B.
Khẳng định nào sau đây là đúng?
A. Số \(0\) không phải là một đa thức . Sai Vì số 0 là đa thức 0
B. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường thẳng. Đúng: (vẽ một tam giác cân và xác định trọng tâm, trực tâm, điểm cách đều 3 đỉnh, điểm nằm trong tam giác và cách đều 3 cạnh ta thấy chúng cùng nằm trên một đường thẳng)
C. Nếu \(\Delta ABC\) cân thì trọng tâm, trực tâm, điểm cách đều ba đỉnh, điểm (nằm trong tam giác) cách đều ba cạnh cùng nằm trên một đường tròn. Sai Vì chúng nằm trên cùng 1 đường thẳng.
D. Số \(0\) được gọi là một đa thức không và có bậc bằng 0. Sai Vì số 0 được gọi là đa thức không và nó là đa thức không có bậc.
Chọn B
Điểm thi đua các tháng trong năm học 2013-2014 của lớp 7A được ghi trong Bảng 1:
Tần số của điểm 8 là:
Trong bảng 1, điểm 8 xuất hiện 3 lần.
Vậy tần số của điểm 8 là 3.
Chọn B
Mốt của dấu hiệu điều tra trong bảng 1 là :
Trong bảng 1 ta thấy điểm 8 xuất hiện với tần số lớn nhất là 3.
Vậy mốt của dấu hiệu là : điểm 8
Chọn B
Đơn thức nào sau đây đồng dạng với đơn thức \( - 3x{y^2}\)
Đơn thức khác hệ số và có cùng phần biến với đơn thức \( - 3x{y^2}\)là: \(\left( { - 3xy} \right)y = {\rm{\;}} - 3x{y^2}\)
Chọn B
Kết quả của phép tính \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5}\)
Ta có: \( - 5{x^2}{y^5} - {x^2}{y^5} + 3{x^2}{y^5} = \left( { - 5 - 1 + 3} \right){x^2}{y^5} = {\rm{\;}} - 3{x^2}{y^5}\)
Chọn A.
Giá trị của biểu thức \(3{x^2}y + 3{x^2}y\) tại \(x = {\rm{\;}} - 2\) và \(y = {\rm{\;}} - 1\) là:
Thu gọn đa thức ta được: \(3{x^2}y + 3{x^2}y = 6{x^2}y\)
Thay \(x = {\rm{\;}} - 2;{\mkern 1mu} y = {\rm{\;}} - 1\) vào biểu thức đã được thu gọn ta có: \(6.{\left( { - 2} \right)^2}\left( { - 1} \right) = {\rm{\;}} - 24\)
Chọn D
Tam giác có một góc \({60^0}\) thì với điều kiện nào thì trở thành tam giác đều :
Tam giác có một góc bằng \({60^0}\)và có hai cạnh bằng nhau là tam giác đều.
Chọn B
Bậc của đa thức \(A = {\rm{\;}} - 3{x^5} - \frac{1}{2}{x^3}y - \frac{3}{4}x{y^2} + 3{x^5} + 2 - \frac{3}{4}{x^2}y\) là:
Ta có:
\(\begin{array}{*{20}{l}}{A = {\rm{\;}} - 3{x^5} - \frac{1}{2}{x^3}y - \frac{3}{4}x{y^2} + 3{x^5} + 2 - \frac{3}{4}{x^2}y}\\{A = \left( { - 3{x^5} + 3{x^5}} \right) - \frac{1}{2}{x^3}y - \frac{3}{4}x{y^2} - \frac{3}{4}{x^2}y}\\{A = {\rm{\;}} - \frac{1}{2}{x^3}y - \frac{3}{4}x{y^2} - \frac{3}{4}{x^2}y}\end{array}\)
Bậc của \({x^3}y\) là 4. Bậc của \(x{y^2}\) là 3. Bậc của \({x^2}y\) là 3.
Vậy bậc của đa thức \(A\) là 4.
Chọn B.
Giá trị của a,b để đơn thức \(\frac{1}{2}{x^a}{y^{b + 1}}\) đồng dạng với đơn thức \(2{x^2}{y^3}\) là:
Để đơn thức \(\frac{1}{2}{x^a}{y^{b + 1}}\) đồng dạng với đơn thức \(2{x^2}{y^3}\) thì:
\(\left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b + 1 = 3}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 2}\end{array}} \right.\)
Vậy \(a = 2;b = 2\)
Chọn C.
Giá trị của biểu thức \(A = xy - 2{x^3}{y^4} - {x^{2019}} + 3y\) tại \(x = {\rm{\;}} - 1;y = 2\) là:
Thay \(x = {\rm{\;}} - 1;y = 2\) vào biểu thức \(A = xy - 2{x^3}{y^4} - {x^{2019}} + 3y\) ta có:
\(\begin{array}{*{20}{l}}{A = xy - 2{x^3}{y^4} - {x^{2019}} + 3y}\\{A = \left( { - 1} \right).2 - 2.{{\left( { - 1} \right)}^3}.\left( {{2^4}} \right) - {{\left( { - 1} \right)}^{2019}} + 3.2}\\{A = {\rm{\;}} - 2 + 32 + 1 + 6}\\{A = 37}\end{array}\)
Vậy \(A = 37\) tại \(x = {\rm{\;}} - 1;{\mkern 1mu} y = 2\)
Chọn B.
Cho \(\Delta ABC\) có \(\angle B = {45^0},\angle C = {75^0}.\) Tia AD là tia phân giác của \(\angle BAC\left( {D \in BC} \right).\) Khi đó số đo của \(\angle ADB\) là:
Theo định lý tổng ba góc của một tam giác, trong \(\Delta ABC\) ta có:
\(\begin{array}{*{20}{l}}{\angle BAC = {{180}^0} - \left( {\angle B + \angle C} \right)}\\{ = {{180}^0} - \left( {{{45}^0} + {{70}^0}} \right)}\\{ = {{60}^0}}\end{array}\)
Vì AD là tia phân giác của \(\angle BAC\) nên \(\angle {A_1} = \angle {A_2} = \frac{{\angle BAC}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\).
Xét \(\Delta ABD\) có:
\(\begin{array}{*{20}{l}}{\angle BDA = {{180}^0} - \left( {\angle B + \angle {A_1}} \right)}\\{ = {{180}^0} - \left( {\angle {{45}^0} + {{30}^0}} \right)}\\{ = {{105}^0}}\end{array}\)
Chọn A.
Tam giác ABC có \(BC = 1cm,{\mkern 1mu} AC = 8cm.\) Tìm độ dài cạnh AB, biết độ dài này là một số nguyên \(\left( {cm} \right)\).
Áp dụng bất đẳng thức cho tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{AC - BC < AB < AC + BC}\\{ \Rightarrow 8 - 1 < AB < 8 + 1}\\{ \Rightarrow 7 < AB < 9}\\{ \Rightarrow AB = 8\left( {cm} \right)}\end{array}\)
Chọn C.
Điểm kiểm tra một tiết môn Toán của lớp 7A được ghi lại trong bảng sau:
Số các giá trị của dấu hiệu là bao nhiêu?
Dấu hiệu: Điểm kiểm tra 1 tiết môn toán của mỗi bạn học sinh trong lớp 7A.
Số các giá trị của dấu hiệu là: 40.
Kết quả thu gọn đơn thức \(\left( { - \frac{3}{4}{x^2}y} \right).\left( { - x{y^3}} \right)\) là:
Ta có: \(\left( { - \frac{3}{4}{x^2}y} \right).\left( { - x{y^3}} \right) = \left( {\frac{{ - 3}}{4}.\left( { - 1} \right)} \right).{x^2}.x.y.{y^3} = \frac{3}{4}.{x^3}.{y^4}.\)
Chọn C.
Giá trị của đa thức \(P = {x^2}y + 2xy + 3\) tại \(x = {\rm{\;}} - 1,{\mkern 1mu} y = 2\) là
Thay \(x = {\rm{\;}} - 1,{\mkern 1mu} y = 2\) vào đa thức \(P\) ta có:
\(P\left( { - 1;2} \right) = {\left( { - 1} \right)^2}.2 + 2.\left( { - 1} \right).2 + 3 = 2 - 4 + 3 = 1.\)
Chọn B.
Tổng của hai đơn thức \(4{x^2}y\) và \( - 8{x^2}y\) là:
Ta có: \(4{x^2}y + \left( { - 8{x^2}y} \right) = \left( {4 + \left( { - 8} \right)} \right).{x^2}y = {\rm{\;}} - 4.{x^2}y\).
Chọn C.
Cho \(\Delta ABC\) có \(AB = 6cm,{\mkern 1mu} BC = 8cm,{\mkern 1mu} AC = 10cm.\) Số đo góc \(\angle A;{\mkern 1mu} \angle B;{\mkern 1mu} \angle C\) theo thứ tự là:
\(\Delta ABC\) có \(AB = 6cm,{\mkern 1mu} BC = 8cm,{\mkern 1mu} AC = 10cm.\)
Ta có: \(AB < BC < AC\) \( \Rightarrow \angle C < \angle A < \angle B\)
Chọn B.
Số lượng học sinh giỏi của một trường trung học cơ sở được ghi lại bởi bảng dưới đây:
Số các giá trị khác nhau của dấu hiệu là:
Có 7 giá trị khác nhau của dấu hiệu là 7, 8, 9, 10, 11, 12, 15.
Đáp án cần chọn là: B
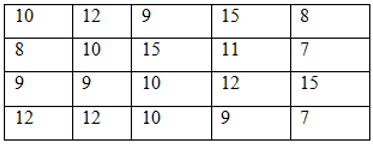
Điều tra về sự tiêu thụ điện năng (tính theo kwh) của một số gai đình ở một tổ dân số, ta có kết quả sau:
Có bao nhiêu hộ gia đình tiêu thụ với mức điện năng nhỏ hơn 100 kwh?
Có 12 hộ gia đình tiêu thụ với mức điện năng nhỏ hơn 100 kwh
Đáp án cần chọn là: D
Biểu thức đại số là:
Biểu thức đại số là biểu thức bao gồm các phép toán trên các số (kể cả những chữ đại diện cho số)
Đáp án cần chọn là: B
Điền cụm từ thích hợp vào chỗ trống: "Trong biểu thức đại sô, những chữ số đại diện cho một số tùy ý được gọi là: ..., những chữ đại diện cho một số xác định được gọi là:..."
Trong biểu thức đại số, những chữ đại diện cho một số tùy ý được gọi là: biến số, những chữ đại diện cho một số xác định được gọi là: hằng số.
Đáp án cần chọn là: B
Nam mua 10 quyển vở, mỗi quyển giá x đồng và hai bút bi, mỗi chiếc giá y đồng. Biểu thức biểu thị số tiền Nam phải trả là
Số tiền Nam phải trả cho 10 quyển vở là 10x (đồng)
Số tiền Nam phải trả cho 2 chiếc bút bi là 2y (đồng)
Nam phải trả tất cả số tiền là 10x + 2y (đồng)
Đáp án cần chọn là: D
Giá trị của biểu thức \({x^3}\; + {\rm{ }}2{x^2}\; - {\rm{ }}3x\) tại x = 2 là:
Thay x = 2 vào biểu thức x3 + 2x2 - 3x ta có:
23 + 2.22 - 3.2 = 8 + 8 - 6 = 10
Đáp án cần chọn là: A
Cho xyz = 4 và x + y + z = 0. Tính giá trị biểu thức M = (x+y)(y+z)(x+z)
Từ x + y + z = 0 ⇒ x + y = -z; y + z = -x; x + z = -y thay vào M ta được:
M = (x+y)(y+z)(x+z) = (-z).(-x).(-y) = -xyz
Mà xyz = 4và x + y + z = 0 thì M = -4
Đáp án cần chọn là: C
Trong các biểu thức đại số sau, biểu thức nào không phải đơn thức?
Biểu thức 5x + 9 không phải là đơn thức
Đáp án cần chọn là: B
Tính giá trị của đơn thức \(5{x^4}{y^2}{z^3}\) tại x = -1; y = -1; z = -2
Thay x = -1; y = -1; z = -2 vào đơn thức 5x4y2z3 ta được: 5(-1)4.(-1)2.(-2)3 = -40
Đáp án cần chọn là: C
Chọn câu trả lời đúng nhất. Ba cạnh của tam giác có độ dài là 6cm; 7cm; 8cm. Góc lớn nhất là góc
Vì trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn mà cạnh 8cm là cạnh lớn nhất trong tam giác nên góc lớn nhất là góc đối diện với cạnh có độ dài 8cm
Đáp án cần chọn là: C
Cho ba điểm a, b, c thẳng hàng và B nằm giữa A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H. Khi đó:
Vì BH là đường vuông góc và AH là đường xiên nên AH > BH
Đáp án cần chọn là: C
Em hãy chọn cụm từ thích hợp điền vào chỗ trống: "Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì ..."
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn.
Đáp án cần chọn là: C
Cho ΔABC có cạnh AB = 1cm và cạnh BC = 4cm. Tính độ dài cạnh AC biết AC là một số nguyên
Gọi độ dài cạnh AC là x (x > 0). Theo bất đẳng thức tam giác ta có:
4 - 1 < x < 4 + 1 ⇔ 3 < x < 5. Vì x là số nguyên nên x = 4. Vậy độ dài cạnh AC = 4cm
Đáp án cần chọn là: D
Thời gian giải bài toán (tính theo phút) của học sinh lớp 7 được ghi lại trong bảng sau:
Giá trị lớn nhất của dấu hiệu ở đây là bao nhiêu? Tìm tần số của nó
Giá trị lớn nhất của dấu hiệu là 10, tần số là 3
Đáp án cần chọn là: C
Biểu thức n.(n + 1).(n + 2) với n là số nguyên, được phát biểu là:
Với số nguyên n thì ba số n.(n + 1).(n + 2) là ba số nguyên liên tiếp.
Biểu thức n.(n + 1).(n + 2) với n là số nguyên, được phát biểu là tích của ba số nguyên liên tiếp .
Đáp án cần chọn là: B
Một bể đang chứa 120 lít nước, có một vòi chảy được x lít. Cùng lúc đó một vòi khác chảy từ bể ra. Một phút lượng nước chảy ra bằng 1/2 lượng nước chảy vào. Hãy biểu thị lượng nước trong bể sau khi đồng thời mở cả hai vòi trên sau a phút
Lượng nước chảy vào bể trong aa phút là a.x (lít)
Lượng nước chảy ra trong a phút là \(\frac{1}{2}ax\) (lít)
Vì ban đầu bể đang chứa 120 lít nước nên lượng nước có trong bể sau aa phút là:
\(120 + ax - \frac{1}{2}ax = 120 + \frac{1}{2}ax\) (lít)
Đáp án cần chọn là: C
Để biểu thức đại số 25 - x2 có giá trị bằng 0 thì
\(25{\rm{ }} - {\rm{ }}{x^2} = 0 = > {x^2} = 25 = > \left[ \begin{array}{l}
x = 5\\
x = - 5
\end{array} \right.\)
Đáp án cần chọn là: D
Tìm phần biến trong đơn thức \(100ab{x^2}yz\) với a,b là hằng số
Đơn thức 100abx2yz với a,b là hằng số có phần biến là x2yz
Đáp án cần chọn là: C
Cho ΔMNP có MN < MP < NP. Trong các khẳng định sau, câu nào đúng?
Vì ΔMNP có MN < MP < NP nên theo quan hệ cạnh và góc trong tam giác ta có \(\widehat P < \widehat N < \widehat M\)
Đáp án cần chọn là: C
Cho ΔABC có 90° < Â < 180°. Trên cạnh AB và AC lấy tương ứng hai điểm M và N (M, N không trùng với các đỉnh của ΔABC). Chọn đáp án đúng nhất
Từ B kẻ BH vuông góc với AC, vì \(\widehat {BAC}\) là góc tù nên H nằm ngoài đoạn thẳng AC
Khi đó BA,BN,BC là đường xiên kẻ từ B đến AC,HA,HN,HC lần lượt là các hình chiếu của BA,BN,BC trên AC
Ta có: HA < HN < HC nên BA < BN < BC (quan hệ giữa đường xiên và hình chiếu)
Từ C kẻ CK vuông góc với AC, vì \(\widehat {BAC}\) là góc tù nên K nằm ngoài đoạn thẳng AB
Khi đó CA,CM,CB à các đường xiên kẻ từ C đém AB,AK,KM,KB lần lượt là các hình chiếu của CA,CM,CB trên AB
Ta có: KA < KM < KB nên CA < CM < CB (quan hệ giữa đường xiên và hình chiếu)
Chọn D
Cho tam giác ABC biết AB = 1cm; BC = 9cm và cạnh AC là một số nguyên. Chu vi ABC là
Gọi độ dài cạnh AC là x (x > 0).
Theo bất đẳng thức tam giác ta có:
9-1 < x < 9+1⇔8 < x < 10. Vì x là số nguyên nên x=9. Độ dài cạnh AC=9cm
Chu vi tam giác ABC là AB + AC + BC = 1 + 9 + 9 = 19cm
Đáp án cần chọn là: C

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
