Đề thi giữa HK1 môn Toán 7 năm 2020 - Trường THCS Lê Quý Đôn
-
Hocon247
-
30 câu hỏi
-
60 phút
-
47 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Số hữu tỉ là số được viết dưới dạng phân số \(\frac ab\) với
Số hữu tỉ là số được viết dưới dạng phân số \(\frac ab\) trong đó a, b ∈ Z, b ≠ 0.
Vậy chọn B.
Cho số hữu tỉ \(x = \frac{{a - 3}}{2}\). Với giá trị nào của a thì x là số nguyên dương.
Để số hữu tỉ \(x = \frac{{a - 3}}{2}\) là số nguyên dương thì (a - 3) > 0 và (a - 3) chia hết cho 2.
Giả sử a - 3 = 2k (k∈ N*) suy ra a = 3 + 2k (k∈ N*)
Vậy chọn D.
Giá trị của x trong phép tính \(\frac{3}{4} - x = \frac{1}{3}\) là:
\(\begin{array}{l} \frac{3}{4} - x = \frac{1}{3}\\ \Leftrightarrow x = \frac{3}{4} - \frac{1}{3}\\ \Leftrightarrow x = \frac{9}{{12}} - \frac{4}{{12}}\\ \Leftrightarrow x = \frac{5}{{12}} \end{array}\)
Vậy chọn B.
Số \(-\frac23\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
biểu diễn số \(-\frac23\) được trên trục số ta được:
Vậy chọn D.
Kết quả thực hiện phép tính \(\frac{{ - 3}}{8} + \frac{1}{4}:2\) là:
\(\frac{{ - 3}}{8} + \frac{1}{4}:2 = \frac{{ - 3}}{8} + \frac{1}{{4.2}} = \frac{{ - 3}}{8} + \frac{1}{8} = \frac{{ - 2}}{8} = \frac{{ - 1}}{4}\)
Vậy chọn C.
Tìm số x thỏa mãn: \(x:\left( {\frac{2}{5} - 1\frac{2}{5}} \right) = 1\)
\(\begin{array}{l} x:\left( {\frac{2}{5} - 1\frac{2}{5}} \right) = 1\\ x:\left( {\frac{2}{5} - \frac{7}{5}} \right) = 1\\ x:\left( { - \frac{5}{5}} \right) = 1\\ x:( - 1) = 1\\ x = - 1 \end{array}\)
Vậy chọn B.
Cách viết nào sau đây là đúng?
A. Sai, sửa lại |−0, 25| = 0, 25
B. Sai, sửa lại − |−0, 25| = −(0, 25)
C. Sai, sửa lại −(−0, 25) = 0, 25
Vậy chọn D.
Giá trị của biểu thức: |− 3, 4| : |1, 7| − 0, 2 là
Ta có:
| − 3, 4| : |1, 7| − 0, 2 = 3, 4 : 1, 7– 0, 2 = 2– 0, 2 = 1, 8
Vậy chọn B.
Kết quả của phép tính (−0, 5).5.(−50).0, 02.(−0, 2).2 là:
Ta có:
(−0, 5).5.(−50).0, 02.(−0, 2).2
= [(−0, 5).2] . [(−50).0, 02] . [5.(−0, 2)]
= (−1).(−1).(−1) = −1
Vậy chọn C.
Có bao nhiêu giá trị x thỏa mãn |x − 3, 5| + |x − 1, 3| = 0?
Vì |x − 3, 5| ≥ 0; |x − 1, 3| ≥ 0 với mọi x nên |x − 3, 5| + |x − 1, 3| ≥ 0 với mọi x
Để |x − 3, 5| + |x − 1, 3| = 0 thì x − 3, 5 = 0 và x − 1, 3 = 0
Suy ra x = 3,5 và x = 1,3 (vô lý vì x không thể đồng thời nhận hai giá trị)
Nên không có x thoả đề bài
Vậy chọn A.
Giá trị của biểu thức A = (5 + 23 - 33)0 là:
Ta có x0 = 1 với mọi x
Do đó A = 1
Vậy chọn D.
Tìm x: (5x - 1)6 = 729
(5x − 1) 6 = 729
(5x − 1) 6 = (3) 6
TH1:
5x − 1 = 3
5x = 4
\(x=\frac45\)
TH2:
5x − 1 = −3
5x = −2
\(x=-\frac25\)
Vậy chọn A.
Tìm số hữu tỉ x biết rằng \(\frac{x}{{{y^2}}} = 2;\frac{x}{y} = 16\left( {y \ne 0} \right)\)
Ta có:
\(\begin{array}{l} \frac{x}{{{y^2}}} = 2\\ \Rightarrow \frac{x}{y}.\frac{1}{y} = 2\\ 16.\frac{1}{y} = 2\\ \frac{1}{y} = \frac{1}{8}\\ y = 8 \end{array}\)
Thay y = 8 vào \(\frac xy=16\) suy ra x = 16.8 = 128
Vậy chọn B.
Cho bốn số 2; 5; a; b với b khác 0 và 2a = 5b, một tỉ lệ thức đúng được thiết lập từ bốn số trên là:
Ta thấy ở đáp án D: \(\frac{2}{b} = \frac{5}{a} \Leftrightarrow 2a = 5b\) nên D đúng
Vậy chọn D.
Tìm hai số x, y biết \(\frac{x}{3} = \frac{y}{5},x + y = - 32\)
Áp dụng dãy tỉ số bằng nhau ta có
\(\begin{array}{l} \frac{x}{3} = \frac{y}{5} = \frac{{x + y}}{{3 + 5}} = \frac{{ - 32}}{8} = - 4\\ \Rightarrow \left\{ \begin{array}{l} \frac{x}{3} = - 4 \Rightarrow x = - 12\\ \frac{y}{5} = - 4 \Rightarrow x = - 20 \end{array} \right. \end{array}\)
Vậy chọn C.
Số học sinh giỏi của lớp 7A, 7B, 7C tỉ lệ với các số 7; 8; 9. Biết số học sinh giỏi của lớp 7C nhiều hơn số học sinh giỏi của lớp 7B là 2 học sinh. Hỏi mỗi lớp có bao nhiêu học sinh giỏi? Số học sinh giỏi của lớp 7A, 7B, 7C lần lượt là:
Gọi số học sinh giỏi của lớp 7A, 7B, 7C lần lượt là x; y; z \(\in\) N*
Vì số học sinh giỏi của các lớp lần lượt tỉ lệ thuận với 7;8;9 nên ta có: \(\frac{x}{7} = \frac{y}{8} = \frac{z}{9}\)
Số học sinh giỏi của lớp 7C nhiều hơn số học sinh giỏi của lớp 7B là 2 học sinh giỏi nên ta có: z - x = 2
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l} \frac{x}{7} = \frac{y}{8} = \frac{z}{9} = \frac{{z - y}}{{9 - 8}} = 2\\ \Rightarrow \left\{ \begin{array}{l} x = 2.7 = 14\\ y = 2.8 = 19\\ z = 2.9 = 18 \end{array} \right. \end{array}\)
Vậy chọn C.
Kết quả làm tròn số 0,737 đến chữ số thập phân thứ hai là:
Làm tròn số 0,737 đến chữ số thập phân thứ hai. Số có chữ số thập phân thứ hai là 3. Chữ số đầu tiên bị bỏ đi là 7 (lớn hơn 5) nên phải cộng thêm 1 vào 3, ta được: 0, 737 ≈ 0, 74 (làm tròn đến chữ số thập phân thứ hai).
Vậy chọn A.
Viết phân số \(\frac{11}{24}\) dưới dạng số thập phân vô hạn tuần hoàn ta được
Ta có: \(\frac{11}{24}=11:24=0,458(3)\)
Vậy chọn A.
Căn bậc hai của 16 là:
Ta có 42 = 16 và (-4)2 = 16
Vậy chọn câu C.
Kết quả của phép tính \(4,2 - \sqrt9\) bằng
Ta có: \(4,2 - \sqrt9=4,2-3=1,2\)
Vậy chọn B.
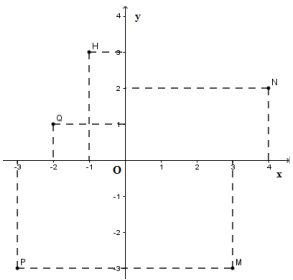
Trong các điểm M (3; −3); N (4; 2); P (−3; −3); Q (−2; 1); H (−1; 3) có bao nhiêu điểm thuộc góc phần tư thứ hai?
Ta thấy có hai điểm thuộc góc phần tư thứ hai là Q ( 2; 1); H ( 1; 3).
Vậy chọn D.
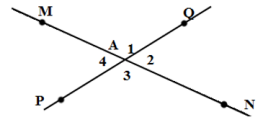
Hai đường thẳng MN và PQ cắt nhau tại A. Biết \(\widehat {MAQ} + \widehat {NAP} = {250^o}\). Tính số đo góc NAP.
Vì AM là tia đối của AN, AQ là tia đối của AP
\(\Rightarrow \widehat {MAQ} = \widehat {NAP}\)
Mà \(\widehat {MAQ} + \widehat {NAP} = {250^o}\)
\(\begin{array}{l} \Rightarrow 2\widehat {NAP} = {250^o}\\ \Rightarrow \widehat {NAP} = {125^o} \end{array}\)
Vậy chọn C.
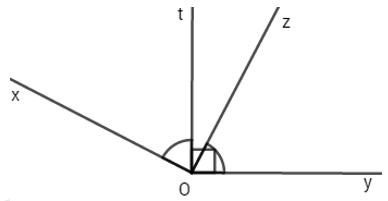
Cho góc tOy có số đo bằng 90o. Vẽ tia Oz nằm trong góc tOy (tia Oz nằm giữa hai tia Ot và Oy). Bên ngoài góc tOy, vẽ tia Ox sao cho \(\widehat {xOt} = \widehat {zOy}\). Tính số đo góc xOz
Vì Oz nằm giữa tia Ot và Oy nên:
\(\begin{array}{l} \widehat {tOz} + \widehat {zOy} = \widehat {tOy}\\ \widehat {tOz} + \widehat {zOy} = {90^o} \end{array}\)
Mà \(\widehat {xOt} = \widehat {zOy} \Rightarrow \widehat {tOz} + \widehat {xOt} =90^o\)
Lại có tia Ot nằm giữa tia Ox và Oz nên \( \widehat {tOz} + \widehat {xOt} = \widehat {xOz} \Rightarrow \widehat {xOz} = {90^o}\)
Vậy chọn C.
Chọn câu đúng.
Tiên đề Ơ-clit: “Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song song với đường thẳng đó.”
Vậy chọn B.
Cho hình vẽ
Em hãy chọn câu đúng nhất trong các câu sau:
A. Đúng
B. Sai, vì đó là hai góc so le trong
C. Sai, vì đó là hai góc đồng vị
D. Sai, vì đó là hai góc so le trong
Vậy chọn A.
Trong các câu sau, câu nào cho một định lí
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Vậy chọn A.
Em hãy chọn phát biểu đúng trong các phát biểu sau:
Các đáp án A, B sai vì cần phải thêm điều kiện: Một đường thẳng cắt hai đường thẳng song song thì tạo ra các cặp góc so le trong và đồng vị bằng nhau.
Vậy chọn câu C.
Cho n (n > 1) đường thẳng phân biệt cắt nhau tại O. Hỏi có bao nhiêu cặp góc đối đỉnh được tạo thành?
Với n đường thẳng phân biệt giao nhau tại 1 điểm có 2n tia chung góc.
Số góc tạo bởi hai tia chung gốc là: 2n (2n − 1) : 2 = n (2n − 1)
Trong đó có n góc bẹt. Số góc còn lại là 2n (n − 1)
Số cặp góc đối đỉnh là n (n − 1)
Vậy chọn A.
Cho đoạn thẳng AB, tập hợp các điểm C sao cho tam giác ABC cân tại C là:
A. Sai vì nếu C trùng với trung điểm của AB thì không tạo thành tam giác.
B. Đúng
C và D Sai vì không tạo thành tam giác có hai cạnh bằng nhau hay hai góc bằng nhau.
Vậy chọn B.

.PNG)