Đề thi giữa HK1 môn Toán 7 năm 2020 - Trường THCS Hoa Lư
-
Hocon247
-
30 câu hỏi
-
60 phút
-
106 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \(\frac 3 {-4}\)?
\(\frac{3}{{ - 4}} = \frac{{3.4}}{{ - 4.4}} = \frac{{12}}{{ - 16}} = \frac{{ - 12}}{{16}}\)
Vậy chọn đáp án C.
Số \(\frac{-5}{12}\) là kết quả của phép tính:
\(\begin{array}{l} \frac{{ - 1}}{6} + \frac{{ - 3}}{{12}} = \frac{{ - 2}}{{12}} + \frac{{ - 3}}{{12}} = \frac{{ - 2 - 3}}{{12}} = \frac{{ - 5}}{{12}}\\ 1 - \frac{{ - 17}}{{12}} = \frac{{12 + 17}}{{12}} = \frac{{29}}{{12}}\\ \frac{{ - 7}}{{12}} + 1 = \frac{{ - 7 + 12}}{{12}} = \frac{5}{{12}}\\ \frac{{ - 1}}{6} - \frac{{ - 3}}{{12}} = \frac{{ - 2}}{{12}} - \frac{{ - 3}}{{12}} = \frac{{ - 2 + 3}}{{12}} = \frac{1}{{12}} \end{array}\)
Vậy chọn đáp án A.
Kết quả của phép tính \(\frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}}\) là
\(\begin{array}{l} \frac{3}{4} + \frac{1}{4}.\frac{{ - 12}}{{20}} = \frac{3}{4} + \frac{{1.( - 12)}}{{4.20}}\\ = \frac{3}{4} + \frac{{1.4.( - 3)}}{{4.20}} = \frac{3}{4} + \frac{{ - 3}}{{20}}\\ = \frac{{15}}{{20}} + \frac{{ - 3}}{{20}} = \frac{{12}}{{20}} \end{array}\)
Giá trị của biểu thức: |-3,4| : |1,7| - 0,2 là:
|-3,4| : |1,7| - 0,2 = 3,4 : 1,7 - 0,2 = 2 - 0,2 = 1,8
Vậy chọn đáp án B.
Viết biểu thức (1,5)3.8 dưới dạng một lũy thừa được kết quả là:
(1,5)3.8 = (1,5)3.23 = (1,5.2)3 = 33
Vậy chọn đáp án D.
Tìm x trong tỉ lệ thức sau: \(\frac{x}{{\frac{3}{{50}}}} = \frac{{\frac{2}{3}}}{x}\)
\(\frac{x}{{\frac{3}{{50}}}} = \frac{{\frac{2}{3}}}{x} \Leftrightarrow {x^2} = \frac{2}{3}.\frac{3}{{50}} \Leftrightarrow {x^2} = \frac{2}{{50}} = \frac{1}{{25}} \Leftrightarrow x = \pm \frac{1}{5}\)
Vậy chọn đáp án D.
Các số x, y thỏa mãn \(\frac x 3 = \frac y 4\) và x - y = 2 là
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{3} = \frac{y}{4} = \frac{{x - y}}{{3 - 4}} = \frac{2}{{ - 1}} = - 2 \Rightarrow \left\{ \begin{array}{l} x = - 2.3 = - 6\\ y = - 2.4 = - 8 \end{array} \right.\)
Vậy chọn đáp án B.
Cho x; y; z là ba số dương phân biệt. Tìm tỉ số \(\frac{x}{y}\) biết \(\frac{y}{{x - z}} = \frac{{x + y}}{z} = \frac{x}{y}\).
\(\frac{y}{{x - z}} = \frac{{x + y}}{z} = \frac{x}{y} = \frac{{y + x + y + x}}{{x - z + z + y}} = \frac{{2x + 2y}}{{x + y}} = 2\)
Vậy chọn đáp án A.
Viết phân số \(\frac {15}{11}\) dưới dạng số thập phân được kết quả là:
\(\frac {15}{11}=1,36363636...=1,(36)\)
Vậy chọn đáp án C.
Trong các số sau đây số nào là số vô tỉ?
Ta có:
\(\sqrt{121}=11\)
0,121212... = 0,(12)
-3,12(345)
⇒ Đều là số hữu tỉ.
0,010010001... là số thập phân vô hạn không tuần hoàn nên nó là số vô tỉ.
Vậy chọn đáp án D.
Phát biểu nào sau đây là sai?
Số thực bao gồm số hữu tỉ và số vô tỉ. Tuy nhiên nếu số thực mà là số hữu tỉ thì sẽ khác số vô tỉ. Do đó phát biểu mọi số thực đều là số vô tỉ là sai.
Vậy chọn đáp án B.
Kết quả so sánh hai số \(x=\frac{-7}8\) và \(y=\frac8{-9}\) là:
Ta có:
\(\begin{array}{l} x = \frac{{ - 7}}{8} = \frac{{ - 7.9}}{{8.9}} = \frac{{ - 63}}{{72}}\\ y = \frac{8}{{ - 9}} = \frac{{ - 8}}{9} = \frac{{ - 8.8}}{{9.8}} = \frac{{ - 64}}{{72}} \end{array}\)
So sánh hai phân số cùng mẫu số ta có:
\(\frac{{ - 63}}{{72}} > \frac{{ - 64}}{{72}} \Leftrightarrow x > y\)
Vậy chọn đáp án B.
Biết y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2. Khi x = - 3 thì giá trị của y bằng bao nhiêu?
Vì y tỉ lệ thuận với x theo hệ số tỉ lệ k = 2.
⇒ y = 2x
Khi x = - 3 thì y = 2.(-3) = - 6
Một nhân viên văn phòng có thể đánh máy được 160 từ trong 2,5 phút. Hỏi cần bao nhiêu phút để người đó đánh được 800 từ (giả thiết rằng thời gian đánh được các từ là như nhau).
Gọi x là thời gian cần thiết để người đó đánh được 800 từ (x > 0).
Vì thời gian và số từ đánh được là hai đại lượng tỉ lệ thuận nên:
\(\frac{x}{{2,5}} = \frac{{800}}{{160}} \Rightarrow x = \frac{{800.2,5}}{{160}} = 12,5\)
Vậy chọn đáp án C.
Công thức nào sau đây cho ta quan hệ tỉ lệ nghịch giữa x và y?
A. 5y =3x ⇒ \(y=\frac{3x}5\) hay đại lượng y tỉ lệ thuận với đại lượng x
B. x và y là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ -2
C. x và y là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 2019
D. x và y không tỉ lệ thuận cũng không tỉ lệ nghịch
Vậy chọn đáp án C.
Điền số thích hợp vào ô trống, biết x và y tỉ lệ nghịch với nhau:
Ta có:
x1 = 5, y1 = ?
x2y2 = x1y1
\({y_1} = \frac{{{x_2}{y_2}}}{{{x_1}}} = \frac{{10.10}}{5} = 20\)
Vậy chọn đáp án B.
Nhận định nào sau đây là đúng: Tập hợp các điểm có hoành độ và tung độ bằng nhau là
Vì điểm đó có tung độ bằng hoành độ ⇒ y = x.
Nên điểm đó nằm trên đường phân giác góc phần tư thứ nhất
Vậy chọn đáp án A.
Điểm thuộc đồ thị hàm số y = -2x là
A. Không thuộc đồ thị hàm số vì với x = -1 thì y = -2.(-1) = 2
B. Không thuộc đồ thị hàm số vì với x = \(\frac12\) thì y = -2.\(\frac12\) = -1
C. Không thuộc đồ thị hàm số vì với x = 0 thì y = -2.0 = 0
D. Thuộc đồ thị hàm số vì với x = -1 thì y = -2. (-1) = 2
Vậy chọn đáp án D.
Cho hàm số \(y = f(x) = \frac{1}{3}{x^2} - 1\) thì
Ta có:
\(\begin{array}{l} f(3) = \frac{1}{3}{3^2} - 1 = 2\\ f(0) = \frac{1}{3}{0^2} - 1 = - 1\\ f( - 1) = \frac{1}{3}{( - 1)^2} - 1 = \frac{{ - 2}}{3} \end{array}\)
Vậy chọn đáp án C.
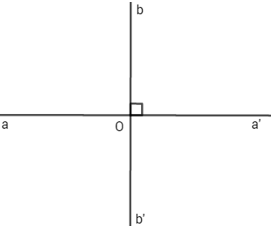
Biết góc xBy có số đo bằng 60o. Tính số đo góc đối đỉnh của góc xBy?
\(\widehat {x'By'} = \widehat {xBy} = {60^o}\)
Vậu chọn đáp án D.
Cho hai đường thẳng aa' và bb' vuông góc nhau tại O. Hãy chỉ ra câu sai trong các câu sau:
A. \(\widehat {aOb} = {90^o}\) → đúng
B. Sai vì aa' và bb' vuông góc nhau nên chúng cắt nhau
C. \(\widehat {a'Ob} = {90^o} = \widehat {a'Ob'}\) → aa' là đường phân giác của góc bẹt bOb'
D. \(\widehat {a'Ob'} = {90^o}\) → đúng.
Vậy chọn đáp án B.
Chọn một cặp góc đồng vị trong hình vẽ sau:
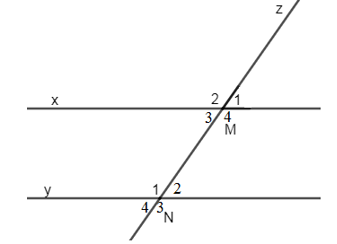
A. Sai vì đó là hai góc so le ngoài
B. Sai vì đó là hai góc so le trong
C. Sai vì đó là hai góc trong cùng phía
D. Đúng
Vậy chọn đáp án D.
Cho hình vẽ sau:
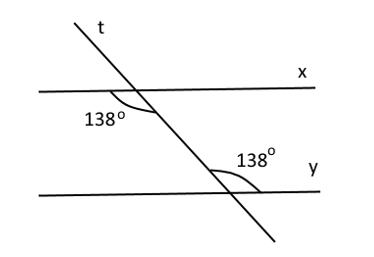
Hãy chọn kết luận đúng:
Từ hình vẽ ta có đường thẳng t cắt hai đường thẳng x và y tạo thành 1 cặp góc so le trong bằng nhau (cùng bằng 138o) nên suy ra x // y.
Vậy chọn đáp án B.
Hãy chọn phát biểu sai trong các phát biểu sau:
A. Đúng theo định nghĩa hai đường thẳng song song
B. Đúng theo tiên đề Ơ-clit
C. Sai vì nó có thể là hai đường thẳng trùng nhau
D. Đúng theo dấu hiệu nhận biết hai đường thẳng song song
Vậy chọn đáp án C.
Cho hai đường thẳng x và y cắt nhau tại O (như hình vẽ).
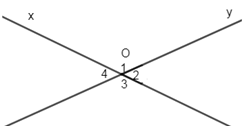
Biết \(\widehat {{O_2}} + \widehat {{O_4}} = {100^o}\). Tính \(\widehat {{O_3}}\)?
Ta có:
\(\widehat {{O_2}} = \widehat {{O_4}}\) (đối đỉnh)
Mà \(\widehat {{O_2}} + \widehat {{O_4}} = {100^o}\) nên \(\widehat {{O_2}} = \widehat {{O_4}}=100^o:2=50^o\)
Lại có: \(\widehat {{O_2}} + \widehat {{O_3}} = {180^o} \Rightarrow \widehat {{O_3}} = {180^o} - {50^o} = {130^o}\)
Vậy chọn đáp án D.
Cho ΔABC = ΔMNP. Chọn đáp án sai
Ta có: ΔABC = ΔMNP
⇒\(\left\{ \begin{array}{l} AB = MN,BC = NP,AC = MP\\ \widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P \end{array} \right.\)
Nên đáp án B sai.
Vậy chọn đáp án B.
Cho ΔABC = ΔMNP. Biết AB = 5cm, MP = 7cm và chu vi của tam giác ABC bằng 22cm. Tính các cạnh còn lại của mỗi tam giác?
Vì ΔABC = ΔMNP nên AB = MN = 5cm; BC = NP; AC = MP = 7cm
Chu vi tam giác ABC: AB + AC + BC = 22 ⇒ BC = 22 - (AB + AC) = 22 - 12 = 10 (cm)
Vậy chọn đáp án C.
Cho hình vẽ sau. Tam giác nào bằng với tam giác ABC?
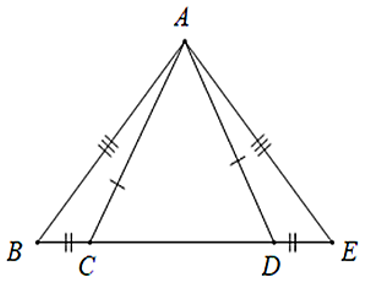
Ta có:
AB = AE
BC = DE
AC = AD
⇒ ΔABC = ΔADE (c.c.c)
Vậy chọn đáp án C.
Cho đoạn thẳng AB = 6cm. Trên một nửa mặt phẳng bờ AB vẽ tam giác ABC sao cho AC = 4cm, BC = 5cm, trên nửa mặt phẳng còn lại vẽ tam giác ABD sao cho BD = 4cm, AD = 5cm. Chọn đáp án đúng?

Từ bài ra ta có: AC = BD = 4cm; BC = AD = 5cm
Xét ΔCAB và ΔDBA có:
AC = BD
AB chung
BC = AD
Do đó: ΔCAB = ΔDBA (c-c-c)
Vậy chọn đáp án C.
Một tam giác cân có góc ở đáy bằng 70° thì góc ở đỉnh bằng bao nhiêu?
Giả sử tam giác ABC cân tại A có góc B = 70o
\(\widehat A = {180^o} - 2\widehat C = {180^o} - {2.70^o} = {40^o}\)
Vậy chọn đáp án D.