Lời giải của giáo viên
 ToanVN.com
ToanVN.com
Gọi phương trình đường thẳng bài cho là: \(d:{\mkern 1mu} {\mkern 1mu} y = ax + b.\)
Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right):{\mkern 1mu} {\mkern 1mu} y = {x^4} - 2{x^2}\) tại hai điểm có hoành độ là \(0;{\mkern 1mu} {\mkern 1mu} 1 \Rightarrow \) tọa độ hai điểm đó là: \(A\left( {0;{\mkern 1mu} 0} \right),{\mkern 1mu} {\mkern 1mu} B\left( {1; - 1} \right).\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a.0 + b = 0}\\{a + b = {\rm{\;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = 0}\\{a = {\rm{\;}} - 1}\end{array}} \right. \Rightarrow d:{\mkern 1mu} {\mkern 1mu} y = {\rm{\;}} - x.\)
Khi đó ta có phương trình hoành độ giao điểm của hai đồ thị hàm số là:
\(\begin{array}{*{20}{l}}{ - x = {x^4} - 2{x^2} \Leftrightarrow {x^4} - 2{x^2} + x = 0 \Leftrightarrow x\left( {{x^3} - 2x + 1} \right) = 0}\\{ \Leftrightarrow x\left( {x - 1} \right)\left( {{x^2} + x - 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 1}\\{{x^2} + x - 1 = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}} \right.}\end{array}\)
Khi đó \(m,{\mkern 1mu} {\mkern 1mu} n\) là hai nghiệm của phương trình \(\left( * \right).\)
Áp dụng hệ thức Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{m + n = {\rm{\;}} - 1}\\{mn = {\rm{\;}} - 1}\end{array}} \right..\)
\( \Rightarrow S = {m^2} + {n^2} = {\left( {m + n} \right)^2} - 2mn = 1 + 2 = 3.\)
Chọn D.
CÂU HỎI CÙNG CHỦ ĐỀ
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ
Hàm số đồng biến trên khoảng:
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right) = 2{x^3} + 3{x^2} - 1\) trên đoạn\(\left[ { - 2; - \dfrac{1}{2}} \right]\). Tính \(P = M - m\).
Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x + 1 - \sqrt {3x + 1} }}{{{x^2} - 3x + 2}}\) là:
Cho hàm số \(y = f(x)\) có đạo hàm \(f'\left( x \right) = 2018{\left( {x - 1} \right)^{2017}}{\left( {x - 2} \right)^{2018}}{\left( {x - 3} \right)^{2019}}\). Tìm số điểm cực trị của \(f(x)\).
Cho hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ. Mệnh đề nào sau đây sai?
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), \(SA = a\), \(AB = a\), \(AC = 2a\), \(BC = a\sqrt 3 .\) Tính thể tích khối chóp S.ABC.
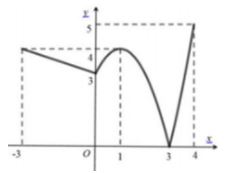
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 3;4} \right]\) và có đồ thị như hình vẽ bên. Gọi \(M\) và \(m\) lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \(\left[ { - 3;4} \right]\). Tính \(M + m\).
Tìm \(m\) để đường thẳng \(y = 2x + m\) cắt đồ thị hàm số \(y = \dfrac{{x + 3}}{{x + 1}}\) tại hai điểm \(M,\;N\) sao cho độ dài MN nhỏ nhất:
Tổng số mặt, số cạnh và số đỉnh của một hình lập phương là:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ
Đồ thị hàm số \(y = \left| {f\left( x \right) - 2m} \right|\) có 5 điểm cực trị khi và chỉ khi
Đồ thị hàm số \(y = \dfrac{{2x - 3}}{{x - 1}}\) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
Cho hình chóp S.ABC có đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt phẳng đáy, \(AB = 2a,{\mkern 1mu} {\mkern 1mu} \widehat {BAC} = {60^0}\) và \(SA = a\sqrt 2 .\) Góc giữa đường thẳng SB và mặt phẳng \(\left( {SAC} \right)\) bằng
Tìm giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^2} - 5}}{{x + 3}}\) trên \(\left[ {0;2} \right].\)
Số tiếp tuyến của đồ thị hàm số \(y = {x^4} - 2{x^2} - 3\) song song với trục hoành là :

.JPG)
.JPG)
.JPG)
.JPG)
