Cho số phức $z = 1 + i + {i^2} + {i^3} + ... + {i^9}$. Khi đó:

Phương trình bậc hai trên tập số phức có thể có mấy nghiệm?

Kí hiệu \(a,b\) lần lượt là phần thực và phần ảo của số phức \(3 - 2\sqrt 2 i\). Tìm \(a,b.\)

Số phức \(w\) là căn bậc hai của số phức \(z\) nếu:

Biết rằng phương trình ${z^2} + bz + c = 0\left( {b;c \in R} \right)$ có một nghiệm phức là ${z_1} = 1 + 2i$ . Khi đó:

Cho số phức $z = 2 + 3i$. Tìm số phức \(w = \left( {3 + 2i} \right)z + 2\overline z \)

Hai số phức \(z = a + bi,z' = a + b'i\) bằng nhau nếu:

Cho số phức $z = a + bi$ với $a,b$ là hai số thực khác $0$. Một phương trình bậc hai với hệ số thực nhận \(\bar z\) làm nghiệm với mọi $a,b$ là:

Cho số phức $z = 3-2i$. Tìm phần thực và phần ảo của số phức \(\overline z \)

Cho số phức $z = 1 + \sqrt {3}i $. Khi đó

Cho phương trình \({z^2} - 2z + 2 = 0\) . Mệnh đề nào sau đây là sai?

Căn bậc hai của số \(a =  - 3\) là:

Cho số phức $z = 2 + 5i$. Tìm số phức \(w = iz + \overline z \).

Cho \({z_1},{z_2}\) là hai nghiệm của phương trình \({z^2} + 2iz + i = 0\). Chọn mệnh đề đúng:

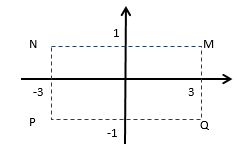
Cho số phức $z$ thỏa mãn $\left( {2-i} \right)z = 7-i$ . Hỏi điểm biểu diễn của $z$ là điểm nào trong các điểm $M,N,P,Q$ ở hình dưới.

Kí hiệu \({z_1},{\rm{ }}{z_2},\,{\rm{ }}{z_3}\) và \({z_4}\) là bốn nghiệm phức của phương trình $6{z^4} + 19{z^2} + 15 = 0.$ Tính tổng \(T = \dfrac{1}{{{z_1}}} + \dfrac{1}{{{z_2}}} + \dfrac{1}{{{z_3}}} + \dfrac{1}{{{z_4}}}.\)

Gọi ${z_1}$, ${z_2}$ là hai nghiệm phức của phương trình ${z^2} - 2z + 2 = 0$. Tính giá trị biểu thức $P = z_1^{2016} + z_2^{2016}.$

Gọi ${z_1},{z_2}$ là các nghiệm của phương trình: $z + \dfrac{1}{z} =  - 1$. Giá trị của $P = {z_1}^3 + {z_2}^3$ là:

Tính môđun của số phức $z$ biết $\overline z  = \left( {4 - 3i} \right)\left( {1 + i} \right)$.

Phương trình: ${z^2} + az + b = 0$ \(\left( {a,b \in \mathbb{R}} \right)\) có một nghiệm phức là $z = 1 + 2i$ . Tổng $2$ số $a$ và $b$ bằng

Cho số phức $z = a + bi$ với $a,b$ là hai số thực khác $0$. Một phương trình bậc hai với hệ số thực nhận \(\bar z\) làm nghiệm với mọi $a,b$ là:

Tìm phần ảo \(b\) của số phức $w = \dfrac{1}{{2i}}\left( {z - \bar z} \right)$ với $z = 5 - 3i$. 

Cho \(z = 1 - 3i\) là một căn bậc hai của \(w =  - 8 - 6i\). Chọn kết luận đúng:

Giả sử ${z_1};{z_2}$ là hai nghiệm phức của phương trình: ${z^2} - 2z + 5 = 0$ và $A,B$ là các điểm biểu diễn của ${z_1};{z_2}$. Tọa độ trung điểm của đoạn thẳng $AB$ là

Chọn mệnh đề đúng:

Cho hai số phức ${z_1} = 3 + 4i,\,\,{z_2} = 4 - 3i$. Mệnh đề nào sau đây là đúng?

Biết rằng có duy nhất một cặp số thực $\left( {x;y} \right)$ thỏa mãn $\left( {x + y} \right) + \left( {x - y} \right)i = 5 + 3i$. Tính \(S = x + y.\)

Gọi ${z_{1,}}$${z_2}$ là các nghiệm phức của phương trình ${z^2} + 4z + 5 = 0$. Đặt $w = {\left( {1 + {z_1}} \right)^{100}} + {\left( {1 + {z_2}} \right)^{100}}$, khi đó

Gọi ${z_1},{z_2}$ là các nghiệm của phương trình: $z + \dfrac{1}{z} =  - 1$. Giá trị của $P = {z_1}^3 + {z_2}^3$ là:

Thu gọn số phức $w = {i^5} + {i^6} + {i^7} + ... + {i^{18}}$ có dạng \(a + bi\). Tính tổng \(S = a + b.\)

Tìm môđun của số phức \(z\), biết \(\dfrac{1}{{{z^2}}} = \dfrac{1}{2} + \dfrac{1}{2}i.\)

Cho phương trình \(2{z^2} - 3iz + i = 0\). Chọn mệnh đề đúng:

Cho \({z_1},{z_2}\) là hai nghiệm của phương trình \({z^2} + 2iz + i = 0\). Chọn mệnh đề đúng:

Kí hiệu \(a,b\) lần lượt là phần thực và phần ảo của số phức \(3 - 2\sqrt 2 i\). Tìm \(a,b.\)

Cho số phức $z = 2 + 3i$. Tìm số phức \(w = \left( {3 + 2i} \right)z + 2\overline z \)

Số phức \(z = a + bi\) có phần thực là:

Căn bậc hai của số \(a =  - 3\) là:

Cho số phức \(z\) thỏa mãn \(5\bar z + 3 - i = \left( { - 2 + 5i} \right)z\). Tính $P = \left| {3i{{\left( {z - 1} \right)}^2}} \right|$.

Gọi \({z_1};{z_2}\) là hai nghiệm phức của phương trình \({z^2} + 2z + 5 = 0\). Tính \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\).

Kí hiệu ${z_1},{z_2},{z_3},{z_4}$ là bốn nghiệm phức của phương trình ${z^4} - {z^2} - 12 = 0$. Tính tổng $T = \left| {{z_1}} \right| + \left| {{z_2}} \right| + \left| {{z_3}} \right| + \left| {{z_4}} \right|$.

Gọi \({z_1};{z_2};{z_3};{z_4}\) là bốn nghiệm phức của phương trình \(2{z^4} - 3{z^2} - 2 = 0\). Tổng \(T = |{z_1}{|^2} + |{z_2}{|^2} + |{z_3}{|^2} + |{z_4}{|^2}\) bằng:

Tính môđun của số phức $z$ biết $\overline z  = \left( {4 - 3i} \right)\left( {1 + i} \right)$.

Cho số phức $z = 1 + i + {i^2} + {i^3} + ... + {i^9}$. Khi đó:

Căn bậc hai của số \(a =  - 3\) là:

Cho số phức $z = 1 + \sqrt {3}i $. Khi đó

Kí hiệu \(a,b\) lần lượt là phần thực và phần ảo của số phức \(3 - 2\sqrt 2 i\). Tìm \(a,b.\)

Cho phương trình \(2{z^2} - 3iz + i = 0\). Chọn mệnh đề đúng:

Cho số phức $z = 3-2i$. Tìm phần thực và phần ảo của số phức \(\overline z \)

Cho phương trình \({z^2} - 2z + 2 = 0\) . Mệnh đề nào sau đây là sai?

Cho số phức $z = a + bi$ với $a,b$ là hai số thực khác $0$. Một phương trình bậc hai với hệ số thực nhận \(\bar z\) làm nghiệm với mọi $a,b$ là: