Đề thi giữa HK2 môn Toán 6 năm 2021 - Trường THCS Tiên Hưng
-
Hocon247
-
40 câu hỏi
-
60 phút
-
64 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Nếu x−c=a−(a+c+b) thì x có kết quả là:
Ta có:
\(\begin{array}{l}x - c = a - (a + c + b)\\x - c = a - a - c - b\\x = a - a - c - b + c\\x = - b\end{array}\)
Tìm số nguyên x, biết rằng tổng của ba số: 17, - 371 và x bằng - 125.
Tổng của ba số: 17, - 371 và x bằng - 125.
Nên:
\(\begin{array}{l}17 + \left( { - 371} \right) + x = - 125\\17 - 371 + x = - 125\\x = 371 - 125 - 17\\x = 229\end{array}\)
Có bao nhiêu số nguyên x thỏa mãn \( \left| {17 + (x - 15) < 4} \right|\)
\( \left| {17 + \left( {x - 15} \right)} \right| < 4 - 4 < 17 + x - 15 < 4 - 4 < x + 2 < 4 - 4 - 2 < x < 4 - 2 - 6 < x < 2\)
Mà x∈Z nên \( x \in \left\{ { - 5, - 4, - 3, - 2, - 1,0,1} \right\}\)
Tìm số nguyên p biết \( 27 - (5 - \left| {p + 1} \right|) = 31\)
\(\begin{array}{l} \begin{array}{*{20}{l}} {27 - (5 - \left| {p + 1} \right|) = 31}\\ {27 - 5 + \left| {p + 1} \right| = 31}\\ {22 + \left| {p + 1} \right| = 31}\\ {\left| {p + 1} \right| = 9} \end{array}\\ TH1:p + 1 = 9 \to p = 8\\ TH2:p + 1 = - 9 \to p = - 10 \end{array}\)
Có bao nhiêu số nguyên x thỏa mãn \( \left| {x + 2} \right| + \left| {x + 8} \right| = x\)
Vì x∈Z nên |x+2|∈N;|x+8|∈ N mà |x+2|+|x+8|=x nên x∈N.
Suy ra x+2 và x+8 dương.
Khi đó \( \left| {x + 2} \right| = x + 2;x + 8 = x + 8\)
Ta có: \(\begin{array}{l} \left| {x + 2} \right| + \left| {x + 8} \right| = x\\ x + 2 + x + 8 = x\\ x + x - x = - 2 - 8\\ x = - 10 \end{array}\) (loại vì x thuộc N)
Vậy không có số nguyên x nào thỏa mãn.
Cho 30(x + 2) - 6(x - 5)- 24x = 100. Tìm x
\(\begin{array}{*{20}{l}} {30(x + 2) - 6(x - 5) - 24{\rm{x}} = 100}\\ {30{\rm{x}} + 60 - 6{\rm{x}} + 30 - 24{\rm{x}} = 100}\\ {(30{\rm{x}} - 6{\rm{x}} - 24{\rm{x}}) + (60 + 30) = 100}\\ {90 = 100(L)} \end{array}\)
Vậy không có x thỏa mãn.
Có bao nhiêu giá trị x thỏa mãn \( \left( {6 - 2x} \right)\left| {7 + x} \right|\left( {2{x^2} + 1} \right) = 0\)
\( \left( {6 - 2x} \right)\left| {7 + x} \right|.\left( {2{x^2} + 1} \right) = 0\)
Vì x2≥0 với mọi x nên \(2x^2+1≥0+1=1\) hay \( 2x^2+1>0\) với mọi x
Suy ra:
\(\begin{array}{*{20}{l}} {(6 - 2{\rm{x}})\left| {7 + x} \right| = 0}\\ {Th1:6 - 2{\rm{x}} = 0}\\ {2{\rm{x}} = 6}\\ {x = 3}\\ {Th2:\left| {7 + x} \right| = 0}\\ {7 + x = 0}\\ {x = - 7} \end{array}\)
Vậy có hai giá trị của x thỏa mãn.
Đáp án cần chọn là: C
Có bao nhiêu giá trị x thỏa mãn (x - 6)(x2 + 2) = 0?
\( \left( {x - 6} \right)\left( {{x^2} + 2} \right) = 0\)
Vì x2≥0 với mọi x nên \(x^2+2≥0+2=2\) hay \(x^2+2>0\) với mọi x
Suy ra
\(x−6=0 \to x=0+6\to x=6\)
Vậy chỉ có 1 giá trị của x thỏa mãn là x=6
Tìm x biết 2(x - 5) - 3(x - 7) = - 2.
\(\begin{array}{*{20}{l}} {2\left( {x - 5} \right) - 3\left( {x - 7} \right) = - 2}\\ {2x - 10 - 3.x + 3.7 = - 2}\\ {2x - 10 - 3x + 21 = - 2}\\ {\left( {2x - 3x} \right) + \left( {21 - 10} \right) = - 2}\\ {\left( {2 - 3} \right)x + 11 = - 2}\\ { - x + 11 = - 2}\\ { - x = - 2 - 11}\\ { - x = - 13}\\ {x = 13} \end{array}\)
Cho \(P = ( - 13) (153 - 45) + 153.( 13 - 45) + 125.( - 2)^3. ( - 1)^{2n} , (n \in N^*)\), chọn câu đúng.
\(\begin{array}{*{20}{l}} {P = ( - 13.153) + (13.45) + (153.13) - (153.45) + 125.{{\left( { - 2} \right)}^3}.{{\left( { - 1} \right)}^{2n}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} }\\ {P = \left[ {(153.13) - (13.153)} \right] + \left[ {(13.45) - (153.45)} \right] + 125.\left( { - 8} \right){\mkern 1mu} .1{\mkern 1mu} {\mkern 1mu} }\\ {P = 0 + 45.(13 - 153) + 125.\left( { - 8} \right)}\\ {P = 45.( - 140) - 1000}\\ {P = - 6300 - 1000}\\ {P = - 7300{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} } \end{array}\)
Tìm x biết: \(147 - \left( {456 - 39} \right)x = 17 - \left( {52 - 15} \right) - 250\)
\(\begin{array}{l}\ \ \,147 - \left( {456 - 39} \right)x = 17 - \left( {52 - 15} \right) - 250\\\,\,\,\,\,147 - 417x = 17 - 37 - 250\\\,\,\,\,\,147 - 417x = - 20 - 250\\\,\,\,\,\,147 - 417x = - 270\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 417x = - 270 - 147\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 417x = - 417\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \left( { - 417} \right):\left( { - 417} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 1\end{array}\)
Tìm x biết: \(\left( {13 - 33} \right)x = 78 - 118\)
\(\begin{array}{l}\ \ \,\left( {13 - 33} \right)x = 78 - 118\\\,\,\,\,\,\, - 20x = - 40\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \left( { - 40} \right):\left( { - 20} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 2\end{array}\)
Tính (−12).(−9) được kết quả là bằng bao nhiêu?
Áp dụng quy tắc nhân hai số nguyên cùng dấu ta có:
(−12).(−9)=∣−12∣.∣−9∣=12.9=108
Cho các phép tính số nguyên như bên dưới, chọn đáp án sai
Đáp án A: (−208).209<0 nên A sai
Đáp án B: (−99).11<0 đúng vì tích hai số nguyên khác dấu là một số nguyên âm.
Đáp án C: 14.(−111)=−1554<−1000 nên C đúng
Đáp án D: (−999).(−888)>0 nên D đúng.
Tính giá trị của biểu thức: A = ax - ay + bx - by biết a + b = - 5;x - y = - 2
\( A = ax - ay + bx - by=a(x-y)+b(x-y)=(x-y)(a+b)\)
Thay \( a + b = - 5;x - y = - 2 \to A = \left( { - 5} \right).\left( { - 2} \right) = 10\)
Cho dãy số: 3;18;48;93;153;….. Số 11703 là số hạng thứ bao nhiêu của dãy.
Từ dãy số ta phá hiện ra qui luật của dãy là: Số liền sau bằng số liền trước cộng với tích của 15 với số thứ tự của số liền trước trong dãy.
Gọi n là số thứ tự của số hạng 11703, ta có:
3+15×1+15×2+15×3+...+(n−1)×15=11703
15×[1+2+3+4+5+...+(n−1)]=11700
\(\begin{array}{l}15 \times \dfrac{{n - 1}}{2} \times n = 1170\\\left( {n - 1} \right) \times n = 1560\\\left( {n - 1} \right) \times n = 39 \times 40\end{array}\)
Suy ra: n = 40.
Tính: \(245.\left( { - 1004 + 247} \right) - 247.\left( {245 - 1004} \right)\)
\(245.\left( { - 1004 + 247} \right) - 247.\left( {245 - 1004} \right)\\ = 245.\left( { - 1004} \right) + 245.247 + \left( { - 247} \right).245 + \left( { - 247} \right).\left( { - 1004} \right)\\ = - 245.1004 + 245.247 - 247.245 + 247.1004\\ = \left( { - 245.1004 + 247.1004} \right) + \left( {245.247 - 247.245} \right)\\ = 1004.\left[ {\left( { - 245} \right) + 247} \right] + 0\\ = 1004.2 = 2008\)
Tính: \(\left( { - 50} \right).3 + 100.50 - 98.\left( {288 - 238} \right)\)
\(\left( { - 50} \right).3 + 100.50 - 98.\left( {288 - 238} \right)\\ = 50.\left( { - 3} \right) + 100.50 + \left( { - 98} \right).50\\ = 50.\left[ {\left( { - 3} \right) + 100 + \left( { - 98} \right)} \right]\\ = 50.\left( { - 1} \right) = - 50\)
Thực hiện phép tính: \(\left( { - 256} \right).3 - 4.256 + 8.256\)
\(\left( { - 256} \right).3 - 4.256 + 8.256\)
\(= 256.\left( { - 3} \right) + \left( { - 4} \right).256 + 8.256\)
\(= 256.\left[ {\left( { - 3} \right) + \left( { - 4} \right) + 8} \right]\)
\(= 256.1 = 256\)
Người ta muốn lót gạch một nền nhà hình chữ nhật có chu vi 32m, có chiều rộng kém chiều dài 4m;4m; bằng những viên gạch vuông cạnh 2dm. Tìm số gạch cần dùng để lót nền nhà đó
Nửa chu vi hình chữ nhật là: 32:2=16m
Suy ra tổng chiều dài và chiều rộng là 16m, hiệu chiều dài và chiều rộng là 4m4m
Chiều dài hình chữ nhật là: (16+4):2=10m
Chiều rộng hình chữ nhật là: 10 - 4 = 6m
Diện tích hình chữ nhật là: 10×6=60m2
Diện tích viên gạch là: 2×2=4dm2=0,04m2
Số viên gạch cần dùng là: 60:0,04=1500 viên.
Đáp số: 1500 viên.
Gọi A là tập hợp các giá trị n∈Z để (n2+2) là bội của (n+2). Số các phần tử của A là bằng bao nhiêu?
Biến đổi biểu thức n2+2 về dạng a.(n+2)+b với b∈Z rồi suy ra n+2 là ước của b
Ta có:
\(\begin{array}{l}{n^2} + 2 = {n^2} + 2n - 2n - 4 + 6\\ = n(n + 2) - 2(n + 2) + 6\\ = (n - 2)(n + 2) + 6\end{array}\)
Vì n∈Z nên để n2+2 là bội của n + 2 thì 6 là bội của n + 2 hay n + 2 là ước của 6
U(6)={±1;±2;±3;±6} nên n+2∈{±1;±2;±3;±6}
Vậy số các phần tử của A là 8
Cho x;y∈Z. Nếu 6x + 11y là bội của 31 thì x + 7y là bội của số nào dưới đây?
Ta có:
\(\begin{array}{l}6x + 11y = 6x + 42y - 31y\\ = \left( {6x + 42y} \right) - 31y\\ = 6\left( {x + 7y} \right) - 31y\end{array}\)
Vì 6x + 11y chia hết cho 31 và 31y chia hết cho 31 nên suy ra 6(x+7y) chia hết cho 31
Mà 6 không chia hết cho 31 nên suy ra x + 7y chia hết cho 31
Vậy nếu 6x + 11y chia hết cho 31 thì x + 7y cũng chia hết cho 31
Hay 6x + 11y là bội của 31 thì x + 7y cũng là bội của 31
Có bao nhiêu số nguyên n thỏa mãn(n−1) là bội của (n+5) và (n+5) là bội của (n−1)?
Vì (n−1) là bội của (n+5) và (n+5) là bội của n - 1
Nên n - 1 khác 0 và n + 5 khác 0
Nên n + 5,n - 1 là hai số đối nhau
Do đó:
(n + 5) + (n - 1) = 0
2n + 5 - 1 = 0
2n + 4 = 0
2n = -4
n=-2
Vậy có 1 số nguyên n thỏa mãn bài toán.
Trong các số đã cho sau, số nào là ước của 15?
Ư(15)={x∈N∣15⋮x}.
Ư(15)={1;3;5;15}.
Chọn A
Tìm tất cả các các bội của 5 trong các số sau: 75;120;67;276;135.
B(5)={5.m∣m∈N}
Vì 75⋮5; 120⋮5; 135⋮5 nên đáp án đúng là B.
Chọn B
Cho tia Oz nằm giữa hai tia (Ox;Oy ). Tia Ox nằm giữa hai tia Oz;Ot. Chọn kết luận đúng.
.png)
Vẽ đường thẳng d cắt Ox,Oy,Oz,Ot lần lượt tại A,B,C,D.
Vì tia Oz nằm giữa hai tia Ox;Oy nên tia Oz cắt AB tại C nằm giữa A và B.
Vì tia Ox nằm giữa hai tia Oz;Ot nên tia Ox cắt CD tại A nằm giữa C và D.
Suy ra điểm A nằm giữa hai điểm B và D hay tia Ox nằm giữa hai tia Oy và Ot.
Đáp án cần chọn là: C
Cho tia Oz nằm giữa hai tia (Ox;Oy ). Tia Ot nằm giữa hai tia (Oz;Oy ). Chọn kết luận đúng.
.png)
Lấy điểm A trên tia Ox, điểm B trên tia Oy. Vì tia Oz nằm giữa hai tia Ox;Oy nên tia Oz cắt đoạn AB tại C nằm giữa A,B.
Tia Ot nằm giữa hai tia Oz;Oy nên tia Ot cắt đoạn CB tại D nằm giữa C;B.
Suy ra điểm C nằm giữa A;D suy ra tia Oz nằm giữa hai tia Ox;Ot.
Cho ba điểm A,B,C không thẳng hàng nằm ngoài đường thẳng a. Biết rằng đường thằng a cắt đoạn AB nhưng không cắt đoạn AC. Kết luận nào sau đây sai?
Theo đề bài đường thẳng a không cắt đoạn thẳng AC nên hai điểm A;C cùng thuộc nửa mặt phẳng bờ a.
Vì đường thẳng a cắt đoạn thẳng AB nên hai điểm A;B nằm khác phía so với đường thẳng a.
Suy ra điểm B và C nằm khác phía so với đường thẳng a.
Đáp án cần chọn là: D
.png)
Cho ba điểm M;N;P không thẳng hàng nằm ngoài đường thẳng d. Biết rằng đường thằng d cắt đoạn MN nhưng không cắt đoạn MP. Kết luận nào sau đây đúng nhất?
Theo đề bài đường thẳng dd không cắt đoạn thẳng MP nên hai điểm M;P cùng thuộc nửa mặt phẳng bờ d.d.
Vì đường thẳng dd cắt đọan MN nên hai điểm M;N nằm khác phía so với đường thẳng d.
Suy ra điểm P và N nằm khác phía so với đường thẳng d.
.png)
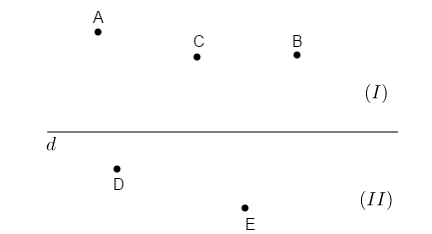
Cho hình vẽ sau:
Kể tên những điểm thuộc nửa mặt phẳng (I) có bờ d
.png)
Ta nối hai điểm AB;AC thấy đoạn AB;AC không cắt đường thẳng d nên ba điểm A;B;C thuộc cùng một nửa mặt phẳng (I) bờ d.
Đáp án cần chọn là: C
Gọi O là giao điểm của bốn đường thẳng xy;zt;uv;ab. Có bao nhiêu góc bẹt đỉnh O?
Các tia Ox và Oy; Ou và Ov; Oz và Ot; Oa và Ob là hai tia đối nhau nên các góc bẹt có đỉnh O là \(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt};\widehat {aOb}\). Vậy có bốn góc bẹt đỉnh O.
Chọn B
Cho n(n≥2) tia chung gốc, trong đó không có hai tia nào trùng nhau. Nếu có 36 góc tạo thành thì n bằng bao nhiêu? Chọn đáp án đúng
Từ đề bài ta có: \(\dfrac{{n\left( {n - 1} \right)}}{2} = 36\) nên n(n - 1) = 72 mà 72 = 9.8 suy ra n = 9.
Vậy n = 9
Chọn D
Cho trước 5 tia chung gốc O. Vẽ thêm 4 tia gốc O không trùng với các tia cho trước. Hỏi đã tăng thêm bao nhiêu góc đỉnh O?
Số góc tạo thành khi có 5 tia chung gốc O là \(\dfrac{{5.(5 - 1)}}{2} = 10\) góc
Số góc tạo thành sau khi thêm 4 tia gốc O không trùng với các tia cho trước là \(\dfrac{{9.(9 - 1)}}{2} = 36\) góc
Số góc tăng thêm là 36 - 10 = 26 góc.
Chọn C
Giả sử có 28 đường thẳng đồng qui tại O thì số góc tạo thành là bằng bao nhiêu?
Vì có 28 đường thẳng đồng qui tại O nên số các tia phân biệt chung gốc O được tạo thành là 2.28 = 56 tia.
Số góc tạo thành là \(\dfrac{{56.(56 - 1)}}{2} = 1540\) góc.
Chọn D
Cho góc xOy khác góc bẹt, tia Oz nằm giữa hai tia Ox;Oy. Tia Ot nằm giữa hai tia Ox;Oz. Lấy điểm (A thuộc Ox; ,B thuộc Oy ), đường thẳng AB cắt tia Oz;Ot theo thứ tự tại M;N . Chọn câu sai.
.png)
Tia Ot nằm giữa hai tia Ox;Oz mà điểm N thuộc tia Ot nên điểm N nằm trong góc xOz. Do đó A đúng.
Tia Ot nằm giữa hai tia Ox;Oz nên điểm N và điểm A nằm cùng phía đối với điểm M
Tia Oz nằm giữa hai tia Ox;Oy nên điểm A;B nằm khác phía đối với điểm M. Suy ra điểm N và điểm B nằm khác phía đối với điểm M, do đó điểm M nằm trong góc yOt. Do đó B đúng, D đúng.
Vì A∈Ox và tia Ot nằm giữa hai tia Ox;Oz nên điểm A không nằm trong góc tOz. Do đó C sai.
Cho hai tia Ox và Oy đối nhau, trên cùng nửa mặt phẳng bờ xy vẽ các tia Oz;Ot sao cho \(\widehat {xOz} = 160^\circ ;\widehat {yOt} = 120^\circ .\) Tia Om là tia phân giác của góc tOz. Tính số đo góc mOz.
Vì Ox và Oy là hai tia đối nhau nên \(\widehat {xOt};\,\widehat {tOy}\) là hai góc kề bù nên \(\widehat {xOt} + \widehat {tOy} = 180^\circ \Rightarrow \widehat {xOt} + 120^\circ = 180^\circ \Rightarrow \widehat {xOt} = 180^\circ - 120^\circ = 60^\circ\)
Lại có \(\widehat {xOt} < \widehat {xOz}\left( {{\rm{do}}\,60^\circ <160^\circ } \right)\) nên tia Ot nằm giữa hai tia Ox và Oz
Do đó \(\widehat {xOt} + \widehat {tOz} = \widehat {xOz} \Rightarrow \widehat {tOz} = \widehat {xOz} - \widehat {xOt} = 160^\circ - 60^\circ = 100^\circ\)
Mà tia Om là tia phân giác của góc tOz nên \(\widehat {mOz} = \dfrac{{\widehat {tOz}}}{2} = \dfrac{{100^\circ }}{2} = 50^\circ\)
Cho hai góc kề bù \(\widehat {aOb}\) và \(\widehat {bOc}\) trong đó \(\widehat {aOb} = 3.\widehat {bOc}\) . Trên nửa mặt phẳng bờ aOc chứa tia Ob, vẽ tia Od sao cho \(\widehat {aOd} = \widehat {bOc}\). Chọn câu đúng về \(\widehat {bOc}\) và \(\widehat {bOd}\)
Ta có \(\widehat {aOb} + \widehat {bOc} = 180^\circ\) (hai góc kề bù)
Mà \(\widehat {aOb} = 3.\widehat {bOc}\) nên \(\widehat {aOb} + \widehat {bOc} = 180^\circ \Rightarrow 3.\widehat {bOc} + \widehat {bOc} = 180^\circ \Rightarrow 4.\widehat {bOc} = 180^\circ \Rightarrow \widehat {bOc} = 180^\circ :4 = 45^\circ\)
Theo đề bài \(\widehat {aOd} = \widehat {bOc}\) mà \(\widehat {bOc} = 45^\circ\) nên \(\widehat {aOd} = 45^\circ\)∘
Lại có \(\widehat {cOd} + \widehat {bOd} + \widehat {aOd} = 180^\circ \Rightarrow 45^\circ + \widehat {bOd} + 45^\circ = 180^\circ \Rightarrow \widehat {bOd} = 180^\circ - 45^\circ - 45^\circ = 90^\circ\)
Vậy \(\widehat {bOc} = 45^\circ ;\,\widehat {bOd} = 90^\circ \Rightarrow \widehat {bOd} = 2\widehat {bOc}.\)
Cho \(\widehat {xOm} = {120^o}\) và góc xOm bằng góc BAC. Khi đó số đo góc BAC bằng bao nhiêu?
Sử dụng: Hai góc bằng nhau có số đo bằng nhau.
Vì \(\widehat {xOm} = \widehat {BAC}\) mà \(\widehat {xOm} = {120^o}\) nên \(\widehat {BAC} = {120^o}\).
Chọn D
Tính góc yOz trên hình vẽ sau biết Oy nằm giữa hai tia Ox;Oz và \(\widehat {xOy} = {45^0};\,\widehat {xOz} = {122^0}\)
.png)
Vì tia Oy nằm giữa hai tia Ox;Oz nên \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) hay \(\widehat {yOz} = \widehat {xOz} - \widehat {xOy} = {122^o} - {45^o} = {77^o}\)
Vậy \(\widehat {yOz} = {77^o}\)
Chọn B
Cho \(\widehat A\) và \(\widehat B\) là hai góc phụ nhau và \(\widehat A = 2\widehat B\). Số đo của mỗi góc là bao nhiêu?
Vì \widehat A và \(\widehat B\) là hai góc phụ nhau nên \(\widehat A + \widehat B = {90^o}\) mà \(\widehat A = 2\widehat B\)
Nên ta có: \(2\widehat B + \widehat B = {90^o}\) hay \(3.\widehat B = {90^o}\) suy ra \(\widehat B = {30^o}\). Khi đó \(\widehat A = {60^o}\)
Vậy \(\widehat A = {60^o};\widehat B = {30^o}\)
Chọn C


.JPG)