Đề thi giữa HK2 môn Toán 6 năm 2021 - Trường THCS Đông Hưng
-
Hocon247
-
40 câu hỏi
-
60 phút
-
149 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Tìm x biết: 7 - x = 8 - (-7)
\(7 - x = 8 - (-7) \)
\( \Rightarrow x = 7 - 8 + \left( { - 7} \right) \Rightarrow x = - 8\)
Khẳng định nào dưới đây là sai?
+) Ta có \(|x + 1| \ge 0\) với mọi \(x \in \mathbb{Z}\) do đó \(2008 - |x + 1| \le 2008\)
Vậy \(2008 - |x + 1|\) có giá trị lớn nhất là \(2008\).
+) Ta có \(|x + 10| \ge 0\) với mọi \(x \in \mathbb{Z}\) do đó \(|x + 10| + 2008 \ge 2008\)
Vậy \(|x + 10| + 2008\) có giá trị nhỏ nhất là \(2008\).
+) \(|x + 10| = x + 10\) nếu \(x + 10 \ge 0 \Rightarrow x \ge - 10.\)
+) \(|x - 10| = x - 10\) nếu \(x - 10 \ge 0 \Rightarrow x \ge 10.\)
Khẳng định nào dưới đây là sai?
Vì nếu \(c = 0\) thì ta không thể suy ra \(a = b.\) Ví dụ: \(1.0 = \left( { - 2} \right).0\) trong đó \(1 \ne \left( { - 2} \right).\)
Nếu a - b = c - b thì đáp án nào sau đây đúng?
Ta có: Nếu a - b = c - b thì a = c
Cho b∈Z và x−(−b)=18. CHo biết x có kết quả nào sau đây?
Ta có:
\(\begin{array}{l}x - ( - b) = 18\\x + b = 18\\x = 18 - b\end{array}\)
Cho các phép tính hai số nguyên khác dấu như sau, hãy chọn câu sai
Đáp án A: (−6).20=−120 nên A đúng.
Đáp án B: 14.(−5)=−70 nên B sai.
Đáp án C: (−35).8=−280 nên C đúng.
Đáp án D: 25.(−20)=−500 nên D đúng.
Cho các phép tính số nguyên như bên dưới, chọn đáp án sai
Áp dụng quy tắc nhân hai số nguyên khác dấu ta có:
(−2019).2020<0 nên A đúng
(−2019).2018<0 nên B đúng
(2018).(−2019)<0 nên C sai
(−2019).2020<−1 nên D đúng
Giá trị nhỏ nhất của biểu thức 3(x + 1)2 + 7 là
Ta có:
\(\begin{array}{l} {\left( {x + 1} \right)^2} \ge 0\forall x \Rightarrow 3.{\left( {x + 1} \right)^2} \ge 0\forall x\\ \Rightarrow 3{\left( {x + 1} \right)^2} + 7 \ge 0 + 7 \Rightarrow 3{\left( {x + 1} \right)^2} + 7 \ge 7 \end{array}\)
Vậy GTNN của biểu thức là 7 đạt được khi: x=−1.
Số giá trị x thuộc Z để (x2 - 5)(x2 - 25) < 0 là:
\(\left( {{x^2} - 5} \right)\left( {{x^2} - 25} \right) < 0\) nên x2−5 và x2−25 khác dấu
Mà \( {x^2} - 5 > {x^2} - 25\) nên \({x^2} - 5 > 0;{x^2} - 25 < 0\)
Suy ra \(x^2>5\) và \(x^2<25\)
Do đó: \(x^2=9 ; x^2=16\)
Từ đó: x∈{±3;±4}
Vậy có 4 giá trị nguyên của x thỏa mãn bài toán.
Cho \(A = (135 - 35).( - 47) + 53.( - 48 - 52) \) và \(B = 25.(75 - 49) + 75.| 25 - 49|. \) Chọn câu đúng.
\(\begin{array}{*{20}{l}} {A = \left( {135 - 35} \right).\left( { - 47} \right) + 53.\left( { - 48 - 52} \right)}\\ { = 100.\left( { - 47} \right) + 53.\left( { - 100} \right)}\\ { = \left( { - 100} \right).47 + 53.\left( { - 100} \right)}\\ { = \left( { - 100} \right).\left( {47 + 53} \right)}\\ { = \left( { - 100} \right).100}\\ { = - 10000} \end{array}\)
Vì 25−49<0 nên \( \left| {25 - 49} \right| = - \left( {25 - 49} \right) = 49 - 25\)
\(\begin{array}{*{20}{l}} {B = 25.\left( {75 - 49} \right) + 75.\left| {25 - 49} \right|}\\ { = 25.\left( {75 - 49} \right) + 75.\left( {49 - 25} \right)}\\ { = 25.75 - 25.49 + 75.49 - 75.25}\\ { = \left( {25.75 - 75.25} \right) + \left( { - 25.49 + 75.49} \right)}\\ { = 0 + 49.\left( { - 25 + 75} \right)}\\ { = 49.50}\\ { = 2450} \end{array}\)
Do đó A và B là hai số nguyên trái dấu.
Kết quả của phép tính 13 . (-5) là:
13 . (-5) = - (13.5) = -65
Kết quả của phép tính (-3) . 7 là:
(-3) . 7 = -(3.7) = -21
Kết quả của phép tính (+3) . (+9) là
(+3) . (+9) = 3.9 = 27
Tìm x biết: \(\left( {256 - 75} \right) + \left( { - 234 + 342} \right)x = - 35\)
\(\begin{array}{l} \ \,\left( {256 - 75} \right) + \left( { - 234 + 342} \right)x = - 35\\\,\,\,\,\,\,181 + 108x = - 35\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,108x = - 35 - 181\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,108x = - 216\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \left( { - 216} \right):108\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = - 2\end{array}\)
Tìm x biết: \(\left( {525 - 725} \right)x = 645 + \left( { - 15 - 30} \right) + 200\)
\(\begin{array}{l}\ \,\left( {525 - 725} \right)x = 645 + \left( { - 15 - 30} \right) + 200\\\,\,\,\,\, - 200x = 645 + \left( { - 45} \right) + 200\\\,\,\,\,\, - 200x = 600 + 200\\\,\,\,\,\, - 200x = 800\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 800:\left( { - 200} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = - 4\end{array}\)
Tính: (-57) . (67 - 34) - 67 . (34 - 57)
(-57) . (67 - 34) - 67 . (34 - 57)
= (-57) . 33 - 67 . (-23)
= -1881 + 1541
= -340
Tính: (37 - 17) . (-5) + 23 . (-13 - 17)
(37 - 17) . (-5) + 23 . (-13 - 17)
= 20 . (-5) + 23 . (-30)
= (-100)+( - 690) = -790
Thực hiện phép tính: 4 . 7 . (-11) . (-2).
4 . 7 . (-11) . (-2)
= [4 . 7 . (-2)] . (-11)
= [28. (-2)] . (-11)
= (-56) . (-11) = 616.
Thực hiện phép tính: 15 . (-2) . (-5) . (-6)
15 . (-2) . (-5) . (-6)
= [15 . (-6)] . [ (-5).(-2)]
= (-90) . 10 = -900.
Tính: \(\left( {58 - 25} \right).203 - 35.89 + 33.\left( { - 103} \right) - 35.11\)
\(\left( {58 - 25} \right).203 - 35.89 + 33.\left( { - 103} \right) - 35.11\\ = 33.203 - 35.89 + 33.\left( { - 103} \right) - 35.11\\ = \left[ {33.203 + 33.\left( { - 103} \right)} \right] + \left[ {\left( { - 35} \right).89 + \left( { - 35} \right).11} \right]\\ = 33.\left[ {203 + \left( { - 103} \right)} \right] + \left( { - 35} \right).\left( {89 + 11} \right)\\ = 33.100 + \left( { - 35} \right).100\\ = 100.\left[ {33 + \left( { - 35} \right)} \right]\\ = 100.\left( { - 2} \right) = - 200\)
Tìm giá trị của x, biết: x⋮7 và 42⋮x.
Ta có:
A=B(7)={0;±7;±14;±21;±28;±35...}
B=U(42)={±1;±2;±3;±6;±7;±14;±21;±42}
Vậy x∈A∩B={±7;±14;±21}.
Tập hợp tất cả các bội của 9 có giá trị tuyệt đối nhỏ hơn 55 là đáp án nào trong các đáp án sau?
Bội của 9 gồm số 0 và các số nguyên có dạng 9k,k∈Z∗
Khi đó các bội nguyên dương của 9 mà nhỏ hơn 55 là: 9;18;27;36;45;54
Vậy tập hợp các bội của 9 có giá trị tuyệt đối nhỏ hơn 55 là: {0;±9;±18;±27;±36;±45;±54}
Tìm giá trị của x, biết: (−15)⋮x và x>3
Tập hợp ước của −15 là: A={±1;±3;±5;±15}
Vì x>3 nên x∈{5;15}
Có bao nhiêu số nguyên x biết: x⋮7 và ∣x∣<45?
Ta có: B(7)={0;±7;±14;±21;±28;±35;±42;±49...}
Vậy các số nguyên x cần tìm là: {0;±7;±14;±21;±28;±35;±42}
Có tất cả 13 số nguyên cần tìm.
Tất cả các ước chung của 25 và - 40 là:
Ta có:
U(25)={±1;±5;±25}
U(−40)={±1;±2;±4;±5;±8;±10;±20;±40}
Vậy UC(25;−40)={±1;±5}
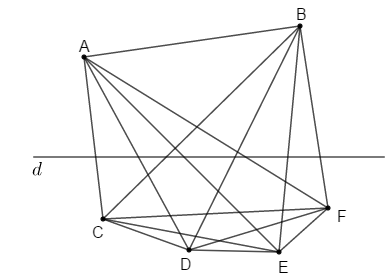
Cho đường thẳng d và sáu điểm A; B; C; D; E; F trong đó A; B thuộc cùng nửa mặt phẳng có bờ d và C; D; E; F cùng thuộc nửa mặt phẳng còn lại có bờ d. Khi đó đường thẳng d cắt bao nhiêu đoạn thẳng?
Vì A;B nằm khác phía với C;D;E;F nên ta có:
+) A và C nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn AC.
+) A và D nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn AD.
+) A và E nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn AE.
+) A và F nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn AF
+) B và C nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn BC.
+) B và D nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn BD.
+) B và E nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn BE
+) B và F nằm khác phía so với đường thẳng d suy ra đường thẳng dd cắt đoạn BF.
Vậy đường thẳng d cắt tám đoạn thẳng AC;AD;AE;AF;BC;BD;BE;BF.
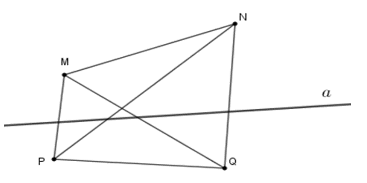
Cho đường thẳng a và bốn điểm M;N;P;Q trong đó M;N thuộc cùng nửa mặt phẳng có bờ a và P;Q cùng thuộc nửa mặt phẳng còn lại có bờ a. Khi đó đường thẳng a cắt bao nhiêu đoạn thẳng?
Vì M;N nằm khác phía với P;Q nên ta có
+) P và M nằm khác phía so với đường thẳng a suy ra đường thẳng a cắt đoạn PM.
+) P và N nằm khác phía so với đường thẳng a suy ra đường thẳng a cắt đoạn PN.
+) Q và M nằm khác phía so với đường thẳng a suy ra đường thẳng a cắt đoạn QM.
+) Q và N nằm khác phía so với đường thẳng a suy ra đường thẳng a cắt đoạn QN.
Vậy đường thẳng a cắt bốn đoạn thẳng PM;PN;QM;QN.
Đáp án cần chọn là: D
Cho đường thẳng d, điểm O thuộc d và điểm M không thuộc d. Gọi N là điểm bất kì thuộc tia OM (N khác O). Chọn câu đúng.
Vì O∈d và M∉d nên tia OM cắt đường thẳng d tại O.
Mà N thuộc tia OM nên suy ra M và N nằm cùng phía so với đường thẳng d hay đoạn thẳng MN không cắt đường thẳng d.
Trên đường thẳng d lấy bốn điểm lần lượt theo thứ tự là: M, N, P, Q. Từ điểm O nằm ngoài đường thẳng d nối với các điểm M, N, P, Q. Hãy chỉ ra đáp án sai.
Ta có:
+ Tia ON cắt đoạn thẳng MP và điểm N nằm giữa hai điểm M và P
⇒ Tia ON nằm giữa hai tia OM và OP.
+ Tia OP cắt đoạn thẳng MQ và điểm P nằm giữa hai điểm M và Q
⇒ Tia OP nằm giữa hai tia OM và OQ.
+ Tia OP cắt đoạn thẳng NQ và điểm P nằm giữa hai điểm N và Q
⇒ Tia OP nằm giữa hai tia ON và OQ
+ Tia ON cắt đoạn thẳng MQ và điểm N nằm giữa hai điểm M và Q
⇒ Tia ON nằm giữa hai tia OM và OQ. (đáp án D sai)
Đáp án cần chọn là: D
Trên đường thẳng a lấy bốn điểm lần lượt theo thứ tự là: A, B, C, D. Từ điểm O nằm ngoài đường thẳng a nối với các điểm A, B, C, D. Hãy chỉ ra đáp án đúng nhất?
.png)
Ta có:
+ Tia OB cắt đoạn thẳng AC và điểm B nằm giữa hai điểm A và C
⇒ Tia OB nằm giữa hai tia OA và OC
+ Tia OC cắt đoạn thẳng AD và điểm C nằm giữa hai điểm A và D
⇒ Tia OC nằm giữa hai tia OA và OD
+ Tia OC cắt đoạn thẳng BD và điểm C nằm giữa hai điểm B và D
⇒ Tia OC nằm giữa hai tia OB và OD.
Đáp án cần chọn là: D
Chọn phát biểu sai trong các phát biểu sau đây.
Ta có góc nhỏ hơn góc vuông là góc nhọn; Góc lớn hơn góc vuông nhưng nhỏ hơn góc bẹt là góc tù nên A đúng, B sai, C đúng.
Số đo của góc bẹt là 180o mà số đo của mỗi góc không vượt quá 80o nên góc bẹt là góc có số đo lớn nhất. Do đó D đúng.
Chọn B
Cho các góc có số đo là: \({35^0};{105^0};{90^0};{60^0};{152^0};{45^0};{89^0}\). Có bao nhiêu góc là góc nhọn?
Sử dụng: Góc có số đo lớn hơn {0^o} và nhỏ hơn {90^o} là góc nhọn.
Ta có: góc có số đo lớn hơn \({0^o}\) và nhỏ hơn \({90^o}\) là góc nhọn nên các góc có số đo \({35^0};{60^0};{45^0};{89^0}\) là các góc nhọn. Vậy có bốn góc nhọn.
Chọn B
Cho 7 tia chung gốc (không có tia nào trùng nhau) thì số góc tạo thành là bao nhiêu?
Sử dụng:
Nếu có n(n≥2) tia chung gốc (không có tia nào trùng nhau) thì số lượng góc tạo thành là 2n(n−1).
Số góc tạo thành là 27.(7−1)=21 góc.
Chọn A
Cho hình vẽ sau. Chọn câu đúng trong các đáp án sau:
.png)
Áp dụng cách đọc góc, phân biệt được đỉnh và cạnh của góc.
Góc trên hình là góc \(\widehat {BAC}\), đỉnh A, cạnh AB và AC.
Chọn B
Kể tên tất cả các góc có một cạnh là AB có trên hình vẽ sau:
.png)
Xác định các tia chung gốc A, từ đó xác định các góc có một cạnh là AB.
Các góc cần tìm là \(\widehat {BAC};\widehat {BAE};\widehat {BAD}\)
Chọn D
Cho hình vẽ. Biết tia Oy nằm giữa hai tia Oz và Ox. Tính số đo góc \(\widehat {xOz}\)
.png)
Nếu tia Oy nằm giữa hai tia Oz và Ox thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
Vì tia Oy nằm giữa hai tia Oz và Ox nên \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
Thay \(\widehat {xOy} = 40^\circ ;\,\widehat {yOz} = 30^\circ\) ta được \(30^\circ + 40^\circ = \widehat {xOz}\) suy ra \(\widehat {xOz} = 70^\circ\)
Cho On là tia phân giác của \(\widehat {mOt}\). Biết \(\widehat {mOn} = {45^0}\), số đo của \(\widehat {mOt}\) là bằng bao nhiêu?
Vì On là tia phân giác của \(\widehat {mOt}\) (gt)
\(\Rightarrow \widehat {mOt} = 2.\widehat {mOn} = {2.45^0} = {90^0}\) (tính chất tia phân giác của 1 góc)
Cho hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù. Biết \(\widehat {xOy} = 76^\circ\) . Gọi Om là tia phân giác của góc yOz. Số đo của góc xOm là bằng bao nhiêu?
Ta có: \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù
Do đó: \(\widehat {xOy} + \widehat {yOz} = 180^\circ\)
Thay \(\widehat {xOy} = 76^\circ\) ta được:
\(76^\circ + \widehat {yOz} = 180^\circ\)
Suy ra \(\widehat {yOz} = 180^\circ - 76^\circ = 104^\circ\)
+ Om là tia phân giác của góc yOz
Do đó:\(\widehat {yOm} = \widehat {mOz} = \dfrac{{\widehat {yOz}}}{2} = \dfrac{{104^\circ }}{2} = 52^\circ\)
+ \(\widehat {mOz} < \widehat {zOx}\,\,\left( {52^\circ < 180^\circ } \right)\) nên tia Om nằm giữa hai tia Oz và Ox
Suy ra: \(\widehat {xOm} + \widehat {zOm} = \widehat {zOx}\) Thay \(\widehat {zOm} = 52^\circ ;\,\widehat {xOz} = 180^\circ\) ta được:
\(\widehat {xOm} + 52^\circ = 180^\circ \Rightarrow \widehat {xOm} = 180^\circ - 52^\circ = 128^\circ\)
Cho \(\widehat {BOC} = 96^\circ\) . A là một điểm nằm trong góc BOC. Biết \(\widehat {BOA} = 40^\circ\). Vẽ tia OD là tia đối của tia OA. Tính số đo góc \(\widehat {COD}\)
Vì điểm A nằm trong góc BOC nên tia OA nằm giữa hai tia OB và OC, do đó:
\(\widehat {BOA} + \widehat {AOC} = \widehat {BOC}\)
Thay \(\widehat {BOA} = 40^\circ ;\,\widehat {BOC} = 96^\circ\)∘ ta được: \(40^\circ + \widehat {AOC} = 96^\circ \Rightarrow \widehat {AOC} = 96^\circ - 40^\circ = 56^\circ\)
Vì OD là tia đối của tia OA nên góc AOC và COD là hai góc kề bù, do đó:
\(\widehat {AOC} + \widehat {COD} = 180^\circ \Rightarrow 56^\circ + \widehat {COD} = 180^\circ \Rightarrow \widehat {COD} = 180^\circ - 56^\circ = 124^\circ\)
Vậy \( \widehat {COD} = 124^\circ . \)
Cho hai góc kề \(\widehat {xOy}\) và \(\widehat {yOz}\), Om và On lần lượt là các tia phân giác của \(\widehat {xOy}\) và \(\widehat {yOz}\). Tính số đo góc mOn biết rằng tổng số đo của hai góc xOy và yOz là 140∘
Từ giả thiết ta có \(\widehat {xOy} + \widehat {yOz} = 140^\circ\)
Vì tia Om là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {yOm} = \dfrac{{\widehat {yOx}}}{2}\)
Lại có tia On là tia phân giác của \(\widehat {zOy}\) nên \(\widehat {yOn} = \dfrac{{\widehat {zOy}}}{2}\)
Mà \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề nhau nên tia Oy nằm giữa hai tia Ox và Oz.
Mà On nằm giữa hai tia Oz và Oy; Om nằm giữa hai tia Ox và Oy nên Oy nằm giữa hai tia Om và On
Từ đó \(\widehat {mOn} = \widehat {yOn} + \widehat {yOm} = \dfrac{{\widehat {zOy}}}{2} + \dfrac{{\widehat {xOy}}}{2} = \dfrac{{\widehat {zOy} + \widehat {xOy}}}{2} = \dfrac{{140^\circ }}{2} = 70^\circ\)


.JPG)