Đề thi HK2 môn Vật Lý 11 năm 2021-2022 - Trường THPT Liễn Sơn
-
Hocon247
-
40 câu hỏi
-
60 phút
-
62 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Một người nhìn hòn sỏi dưới đáy một bể nước thấy ảnh của nó dường như cách mặt nước một khoảng 120cm. Chiết suất của nước là n = 4/3 . Độ sâu của bể nước là
B
C D Đáp án
C
- Hướng dẫn giải
Phương pháp giải:
Từ tỉ lệ số mol X và số mol Ag suy ra đặc điểm của anđehit X là HCHO hoặc anđehit 2 chức.
Từ tỉ lệ Y và Na suy ra ancol Y là ancol 2 chức. Từ đó suy ra công thức của anđehit X.
Giải chi tiết:
Gọi S là hòn sỏi dưới đáy bể, S’ là ảnh của S. Để ảnh rõ nét thì góc tới phải nhỏ
Ta có: \(\frac{\sin i}{\operatorname{s}\text{inr}}=\frac{{{n}_{2}}}{{{n}_{1}}}(1)\)
Mà \(\tan i=\frac{HI}{HS};\operatorname{t}\text{anr}=\frac{HI}{HS'}\Rightarrow \frac{\tan i}{\operatorname{t}\text{anr}}=\frac{HS'}{HS}(2)\)
Vì góc tới nhỏ nên sini ≈ tani ≈i
Từ (1) và (2) ta được \(\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{HS'}{HS}\Rightarrow HS=\frac{{{n}_{1}}}{{{n}_{2}}}HS'=1,6m=16dm\)
Chọn C
Một chùm tia song song hẹp truyền trong không khí tới gặp mặt thoáng của một chất lỏng có chiết suất n với góc tới i = 60° ta có tia phản xạ vuông góc với tia khúc xạ. Góc lệch của tia sáng đi vào chất lỏng là
Do i = i’; tia phản xạ và khúc xạ vuông góc nên i + r = 900=> r = 300
Góc lệch của tia sáng: D = i– r = 600 – 300 = 300
Chọn C
Một tia sáng truyền từ môi trường A vào môi trường B dưới góc tới 90 thì góc khúc xạ là 80. Tính vận tốc ánh sáng trong môi trường A. Biết vận tốc ánh sáng trong môi trường B là 2.105 km/s
Theo định luật khúc xạ ánh sáng: n1sin90 = n2sin80 => n1/n2 = 0,89
Mà v2 = 2.105km/s => v1 = v2n2/n1 = 2.105/0,89 = 2,25.105km/s
Chọn A
Khi ánh sáng truyền từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ hơn thì
Khi ánh sáng truyền từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ hơn thì có thể xảy ra hiện tượng phản xạ toàn phần
Chọn B
Lăng kính có góc chiết quang A = 300 và chiết suất n = \(\sqrt{2}\). Tia ló truyền thẳng ra không khí vuông góc với mặt thứ hai của lăng kính khi góc tới i1 có giá trị:
Tia ló truyền thẳng ra không khí vuông góc với mặt thứ hai của lăng kính => i2 = 0
Ta có: sini2 = nsinr2 => r2 = 0 => r1 = A =300
Mà sini1 = nsinr1 => sini1 = \(\sqrt{2}\) sin300 => i1 = 450
Chọn C
Một lăng kính có tiết diện thẳng là tam giác đều, ba mặt như nhau, chiết suất n =\(\sqrt{3}\) , được đặt trong không khí. Chiếu tia sáng đơn sắc nằm trong mặt phẳng tiết diện thẳng, vào mặt bên của lăng kính với góc tới i= 600. Góc lệch D của tia ló và tia tới bằng
Ta có sini1 = nsinr1 => r1 = 300 => r2 = 300 => i2 = 600
Góc lệch D = i1 + i2 – A = 600
Chọn A
Một người thợ săn cá nhìn con cá dưới nước theo phương thẳng đứng. Cá cách mặt nước 40 cm, mắt người cách mặt nước 60 cm. Chiết suất của nước là 4/3 . Mắt người nhìn thấy ảnh của con cá cách mắt một khoảng là
Gọi S là hòn con cá, S’ là ảnh của con cá. Để ảnh rõ nét thì góc tới phải nhỏ
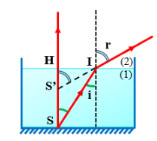
Ta có: \(\frac{\sin i}{\operatorname{s}\text{inr}}=\frac{{{n}_{2}}}{{{n}_{1}}}(1)\)
Mà \(\tan i=\frac{HI}{HS};\operatorname{t}\text{anr}=\frac{HI}{HS'}\Rightarrow \frac{\tan i}{\operatorname{t}\text{anr}}=\frac{HS'}{HS}(2)\)
Vì góc tới nhỏ nên sini ≈ tani ≈i
Từ (1) và (2) ta được \(\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{HS'}{HS}\Rightarrow HS'=\frac{{{n}_{2}}}{{{n}_{1}}}HS=30cm\)
Vậy mắt người thấy cá cách mình 30 + 60 = 90cm
Chọn D
Chiếu một tia sáng đơn sắc từ chân không vào một khối chất trong suốt với góc tới 450 thì góc khúc xạ bằng 300. Chiết suất tuyệt đối của môi trường này là
Định luật khúc xạ ánh sáng n1sini = n2sinr
→ 1.sin450 = n.sin300 → n = \(\sqrt[{}]{2}\)
Chọn C
Một tia sáng truyền trong hai môi trường theo đường truyền như hình vẽ.
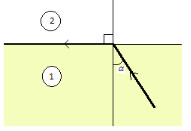
Chỉ ra câu sai.
Định luật khúc xạ ánh sáng n1sinα= n2sin90 = n2 => n2< n1
Nếu ánh sáng truyền từ (2) tới (1) không thể có phản xạ
Chọn D
Ánh sáng truyền trong môi trường có chiết suất n1, tới mặt phân cách với môi trường có chiết suất n2 với góc tới i ≠ 0.
Xét các điều kiện sau:
(1) n2 > n1
(2) n2 < n1
(3) sini ≥ n2/n1
(4) sini ≤ n2/n1
Nếu muốn có phản xạ toàn phần thì (các) điều kiện là
Hiện tượng phản xạ toàn phần xảy ra khi ánh sáng truyền từ môi trường chiết suất lớn sang môi trường có chiết suất nhỏ với góc tới i > igh
Với igh = n2/n1
Chọn D
Vị trí của vật và ảnh cho bởi thấu kính L trường hợp nào sau đây là sai?
Ảnh tạo bởi thấu kính dịch chuyển cùng chiều với vật
Vậy nên nói Cho vật tiến ra xa L, ảnh di chuyển ngược chiều với vật là sai.
Chọn B
Vật sáng đặt trước một thấu kính hội tụ có tiêu cự f, cách thấu kính một khỏang d. Nếu d > f , bao giờ cũng có ảnh
Với thấu kính hội tụ, vật nằm ngoài khoảng tiêu cự luôn cho ảnh thật, ngược chiều vật.
Chọn D
Chọn phát biểu đúng với vật thật đặt trước thấu kính.
Thấu kính phân kì luôn tạo chùm tia ló phân kì
Chọn B
Một lăng kính có chiết suất n, đặt trong không khí, có góc chiết quang A, nhận một tia sáng tới vuông góc với mặt bên AB và tia ló sát mặt bên AC của lăng kính. Chiết suất n của lăng kính xác định bởi
Theo đề bài ta có i = 00, i’ = 900
Sini1 = nsinr1 => r1= 0 => r2 = A
Sini2 = nsinr2 = nsinA => n = \(\frac{1}{\sin A}\)
Chọn A
Một vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự f cho ảnh thật cách thấu kính một đọan d’ =2f. Khi đó khoảng cách từ vật tới ảnh là
Công thức thấu kính: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
Theo đề bài ta có: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{2f}\Rightarrow d=2f\)
Chọn A
Một học sinh bố trí thí nghiệm theo sơ đồ như hình vẽ.
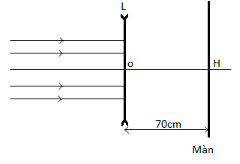
Thấu kính phân kì L có tiêu cự -10 cm. Khoảng cách từ ảnh tạo bởi thấu kính đến màn có giá trị nào?
Theo bài ra: d = ∞ nên cho ảnh tại tiêu điểm => d’ = f = -10cm
Khoảng cách từ ảnh đến màn là 10 + 70 = 80cm
Chọn C
Một người viễn thị có điểm cực cận cách mắt 40cm. Để có thể nhìn thấy vật gần nhất cách mắt 25cm, người đó cần đeo sát mắt một kính có độ tụ bằng
Công thức thấu kính: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
Khi d = 25cm thì d’ = - 40cm \(\Rightarrow \frac{1}{f}=\frac{1}{0,25}-\frac{1}{0,40}=1,5dp\)
Chọn A
Một người cận thị phải đeo sát mắt một kính có độ tụ - 4dp, nhìn rõ được các vật ở vô cực. Điểm cực viễn của mắt người ấy khi không đeo kính cách mắt một khoảng là
Tiêu cự kính phân kỳ người đó phải đeo là f = 1/D = - 0,25m
Vậy điểm cực viễn khi không đeo kính cách mắt 0,25m = 25cm
Chọn C
Trường hợp nào dưới đây, mắt nhìn thấy vật ở xa vô cực?
Mắt tốt có điểm cực viễn ở xa vô cực khi không điều tiết.
Chọn A
Mắt của một người có điểm cực viễn cách mắt 50 cm. Mắt người này
Mắt tốt có điểm cực viễn ở xa vô cực. Người có cực viễn cách mắt 50cm nên bị tật cận thị.
Chọn B
Vật sáng phẳng AB đặt vuông góc với trục chính của một thấu kính cho ảnh lớn gấp 3 lần vật. Khi dịch chuyển vật gần thêm một khoảng 8 cm thì thấy ảnh có độ lớn không đổi. Tính tiêu cự của thấu kính
Ảnh lớn gấp 3 lần vật nên d’ = 3d, h’ = 3h. Ta có: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{3d}=\frac{4}{3d}\Rightarrow f=\frac{3d}{4}\)
Khi dịch chuyển vật lại gần 8cm thì d1 = d – 8, ảnh có độ lớn không đổi nên h’ = 3h => d1’ = 3(d-8)
Ta có: \(\frac{1}{f}=\frac{1}{d-8}+\frac{1}{3(d-8)}=\frac{4}{3d}\Rightarrow d=16cm\Rightarrow f=12cm\)
Chọn C
Một vật sáng phẳng AB có chiều cao H đặt vuông góc với trục chính của thấu kính và ở trước thấu kính. Khi di chuyển thấu kính giữa vật và màn, có hai vị trí cho ảnh rõ nét trên màn. Các ảnh trên màn có chiều cao lần lượt là h1 và h2. Khoảng cách giữa vật sáng và màn ảnh không đổi. Chiều cao H tính theo h1 và h2 là:
Công thức thấu kính: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\Rightarrow d'=\frac{df}{d-f}\Rightarrow d+d'=\frac{{{d}^{2}}}{d-f}=L\Rightarrow d{}^{2}-dL+fL=0\)
Do f không đổi nên có 2 vị trí thấu kính cho ảnh rõ nét trên màn nên d là nghiệm của phương trình bậc 2 trên
\({{d}_{1}}=\frac{d+\sqrt{{{L}^{2}}-4fL}}{2};{{d}_{2}}=\frac{d-\sqrt{{{L}^{2}}-4fL}}{2}\)
Ta có: \(\frac{{{h}_{1}}}{h}=\frac{{{d}_{1}}'}{{{d}_{1}}}=\frac{f}{{{d}_{1}}-f};\frac{{{h}_{2}}}{h}=\frac{{{d}_{2}}'}{{{d}_{2}}}=\frac{f}{{{d}_{2}}-f}\Rightarrow \frac{{{h}_{1}}{{h}_{2}}}{{{h}^{2}}}=1\Rightarrow h=\sqrt{{{h}_{1}}{{h}_{2}}}\)
Chọn B
Thấu kính hội tụ có tiêu cự5 cm. A là điểm vật thật trên trục chính, cách thấu kính10 cm, A’ là ảnh của A. Tính khoảng cách AA’.
Công thức thấu kính: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\Rightarrow \frac{1}{5}=\frac{1}{10}+\frac{1}{d'}\Rightarrow d'=10cm\)
Khoảng cách AA’ là d + d’ = 10 + 10 = 20cm
Chọn D
Vật sáng phẳng, nhỏ AB đặt vuông góc với trục chính của một thấu kính có tiêu cự f =30 cm. Qua thấu kính vật cho một ảnh thật có chiều cao gấp 2 lần vật. Khoảng cách từ vật đến thấu kính là
Vì ảnh thật cao gấp 2 lần vật nên d’ = 2d
Công thức thấu kính: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\Rightarrow \frac{1}{30}=\frac{1}{d}+\frac{1}{2d}=\frac{3}{2d}\Rightarrow d=45cm\)
Chọn B
Khi chiếu tia sáng đơn sắc qua lăng kính có tiết diện là tam giác đều với góc tới i1 = 450 thì góc khúc xạ r1 bằng góc tới r2 ( hình vẽ). Góc lệch của tia sáng qua lăng kính khi đó là
.jpg)
Ta có r1 + r2 = 2r1 = A = 600 => r1 = 300
Sini1 = nsinr1 => n = \(\sqrt{2}\)
nsinr2 = sini2 => \(\sqrt{2}\)sin300 = sini2 => i2 = 450
Góc lệch : D = i1 + i2 – A = 45 + 45 – 60 = 30
Chọn B
Phát biểu định nghĩa đường sức từ.
Đường sức từ là những đường vẽ ở trong không gian có từ trường, sao cho tiếp tuyến tại mỗi điểm có hướng trùng với hướng của từ trường tại điểm đó.
Chọn A
Phát biểu định luật Len – xơ về chiều dòng điện cảm ứng.
Dòng điện cảm ứng xuất hiện trong mạch kín có chiều sao cho từ trường cảm ứng có tác dụng chống lại sự biến thiên của từ thông ban đầu qua mạch kín.
Chọn B
Nêu cấu tạo của lăng kính:
Lăng kính là một khối chất đồng chất thường có dạng lăng trụ tam giác.
Chọn A.
Cho hai dòng điện \({I_1} = {I_2} = 6A\) chạy trong hai dây dẫn dài, song song, cách nhau \(30cm\) theo cùng một chiều (hình vẽ). Xác định cảm ứng từ tổng hợp tại điểm \(M\) nằm trong mặt phẳng chứa hai dây dẫn, cách hai dây lần lượt \(M{O_1} = 10cm,M{O_2} = 20cm\).
.jpg)
Cảm ứng từ tổng hợp tại M: \(\overrightarrow {{B_M}} = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Biểu diễn các vecto cảm ứng từ tại M trên hình vẽ:
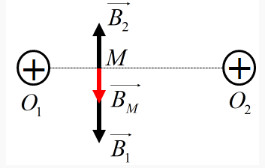
Từ hình vẽ ta có: \(\overrightarrow {{B_1}} \uparrow \downarrow \overrightarrow {{B_2}} \Rightarrow {B_M} = \left| {{B_1} - {B_2}} \right|\)
Với:
\(\left\{ \begin{array}{l}
{B_1} = {2.10^{ - 7}}\frac{{{I_1}}}{{M{O_1}}} = {12.10^{ - 6}}T\\
{B_2} = {2.10^{ - 7}}\frac{{{I_2}}}{{M{O_2}}} = {6.10^{ - 6}}T
\end{array} \right.\)
\( \Rightarrow {B_M} = \left| {{B_1} - {B_2}} \right| = \left| {{{12.10}^{ - 6}} - {{6.10}^{ - 6}}} \right| = {6.10^{ - 6}}T\)
Chọn A.
Một thấu kính hội tụ có tiêu cự 20cm. Tìm vị trí của vật trước thấu kính để ảnh của vật tạo bởi thấu kính gấp 4 lần vật
Ảnh có thể là ảnh thật hoặc ảnh ảo
Áp dụng công thức thấu kính: \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\) . Ta có
Hệ số phóng đại ảnh: \(k=-\frac{d'}{d}=\frac{f}{f-d}\)
+ Nếu ảnh là ảnh thật thì ảnh và vật ngược chiều nên : \(\frac{f}{f-d}=-4\Rightarrow d=\frac{5f}{4}=25cm\)
+ Nếu ảnh là ảnh ảo thì ảnh và vật cùng chiều: \(\frac{f}{f-d}=4\Rightarrow d=\frac{3f}{4}=15cm\)
Chọn D
Một proton bay vào trong từ trường đều theo phương hợp với đường sức từ một góc 300. Vận tốc ban đầu của proton v = 3.107m/s và từ trường có cảm ứng từ B = 1,5T. Tính độ lớn của lực Lorenxo tác dụng lên proton, biết điện tích của proton là q = 1,6.10-19C
Độ lớn lực Lorenxo tác dụng lên proton là:
F = |q|vBsinα = 1,6.10-19.3.107.1,5.sin300 = 3,6.10-12N
Chọn B
Vật sáng AB đặt cách thấu kính một đoạn 20cm cho ảnh A1’B1’ rõ nét trên màn M. Cho vật dịch chuyển một đoạn a = 2cm lại gần thấu kính, ta phải dịch chuyển màn M một đoạn b để lại hứng đượng ảnh A2’B2’ rõ nét trên màn. Biết A2’B2’ = (5/3) A1’B1’. Tính tiêu cự của thấu kính và đoạn dịch chuyển b của màn?
Ảnh thật nên thấu kính là thấu kính hội tụ
Gọi d1, d1’ là khoảng cách từ thấu kính đến vật và ảnh trước khi dịch chuyển, d2, d2’ là khoảng cách từ thấu kính đến vật và ảnh sau khi dịch chuyển
Do ảnh và vật luôn dịch chuyển cùng chiều nên:
d2 = d1 – a = 18cm
d2’ = d1’ + b
Vì ảnh thật nên ngược chiều vật.
Ta có: \(\frac{{{k}_{2}}}{{{k}_{1}}}=\frac{5}{3}\Rightarrow \frac{{{h}_{1}}'}{{{h}_{2}}'}=\frac{5}{3}\Rightarrow \frac{{{d}_{1}}'}{{{d}_{2}}'}=\frac{5}{3}\Rightarrow \frac{f-{{d}_{1}}}{f-{{d}_{2}}}=\frac{5}{3}\Rightarrow f=15cm\)
Vậy \({{d}_{1}}'=\frac{{{d}_{1}}f}{{{d}_{1}}-f}=60cm\)
\({{d}_{2}}'=\frac{{{d}_{2}}f}{{{d}_{2}}-f}=90cm\)
Nên b = d2’ – d1’ = 90 – 60 = 30cm
Chọn D
Chiếu một ánh sáng đơn sắc từ chân không vào môi trường trong suốt với góc tới 450 thì góc khúc xạ bằng 300. Chiết suất tuyệt đối của môi trường này là
Áp dụng biểu thức định luật khúc xạ ánh sáng:
n1sini = n2sinr => sin450 = n.sin300 => n = \(\sqrt{2}\)
Chọn B
Cho một lăng kính thủy tinh có tiết diện là tam giác vuông cân đặt trong không khí, góc chiết quang đối diện với mặt huyền. Nếu góc khúc xạ r1 = 300 thì góc tới r2 = ?
Áp dụng công thức lăng kính: A = r1 + r2 => 900 = 300 + r2 => r2 = 600
Chọn D
Một electron bay vuông góc với các đường sức vào một từ trường đều có độ lớn 10 T thì chịu một lực Lo ren xơ có độ lớn 1,6.10-12N. Vận tốc của electron là
Độ lớn lực lo ren xơ: f = |q|vB
\( \Rightarrow v = \frac{F}{{\left| q \right|B}} = \frac{{1,{{6.10}^{ - 12}}}}{{1,{{6.10}^{ - 19}}.10}} = {1.10^6}\,\,\left( {m/s} \right)\)
Chọn B
Lăng kính có chiết suất \(n = \sqrt 2 \) và góc chiết quang \(A = {60^0}\). Một chùm tia sáng đơn sắc hẹp được chiếu vào mặt bên AB của lăng kính với góc tới \({45^0}\). Tính góc ló của tia sáng khi ra khỏi lăng kính và góc lệch của tia ló và tia tới.
Theo bài ra ta có: \({i_1} = {45^0};n = \sqrt 2 \)
Áp dụng định luật khúc xạ ánh sáng ta có:
\(\sin {i_1} = n.\sin {r_1} \Rightarrow \sin {45^0} = \sqrt 2 .\sin {r_1} \Rightarrow {r_1} = {30^0}\)
Lại có: \(A = {r_1} + {r_2} \Rightarrow {r_2} = A-{r_1} = {60^0}-{30^0} = {30^0}\)
Mặt khác: \(n.\sin {r_2} = \sin {i_2} \Rightarrow \sqrt 2 .\sin {30^0} = \sin {i_2} \Rightarrow {i_2} = {45^0}\)
Góc lệch: \(D = ({i_1} + {\rm{ }}{i_2})-A = {45^0} + {45^0} - {60^0} = {30^0}\)
Chọn B.
Một hạt mang điện chuyển động trong từ trường đều. Mặt phẳng quỹ đạo của hạt vuông góc với đường sức từ. Hạt chuyển động với vận tốc v1 = 1,8.106 m/s. thì lực Lorenxo tác dụng lên hạt có độ lớn f1 = 2.10-6 N. Nếu hạt chuyển động với vận tốc v2 = 4,5.107 m/s thì lực Lorenxo tác dụng lên hạt có độ lớn bằng bao nhiêu.
Độ lớn lực Lorenxo tác dụng lên điện tích: \(F = \left| q \right|vB \Rightarrow F \sim v\)
\( \Rightarrow \frac{{{F_1}}}{{{F_2}}} = \frac{{{v_1}}}{{{v_2}}} \Rightarrow {F_2} = {F_1}.\frac{{{v_2}}}{{{v_1}}} = {2.10^{ - 6}}.\frac{{4,{{5.10}^7}}}{{1,{{8.10}^6}}} = {5.10^{ - 5}}\,\,\left( N \right)\)
Chọn A
Một khung dây hình vuông cạnh 20cm nằm toàn bộ trong một từ trường đều và vuông góc với các đường cảm ứng. Trong thời gian 1/5s, cảm ứng từ của từ trường giảm từ 1,2T về 0. Suất điện động cảm ứng của khung dây trong thời gian đó có độ lớn
Từ thông φ = Bscosα
Suất điện động cảm ứng có độ lớn
\(e=\left| -\frac{\Delta \varphi }{\Delta t} \right|=\left| -\frac{\Delta BS\cos 0}{{}^{1}/{}_{5}} \right|=\frac{{{1,2.0,2}^{2}}}{{}^{1}/{}_{5}}=0,24V=240mV\)
Chọn D
Một thanh dây dẫn dài 20cm chuyển động tịnh tiến trong từ trường đều có B = 5.10-4T. Vec tơ vận tốc của thanh vuông góc với thanh, vuông góc với vec tơ cảm ứng từ và có độ lớn 5m/s. Suất điện động cảm ứng trong thanh là
Suất điện động cảm ứng : e = Blvsinα = 5.10-4.0,2.5.sin90 = 5.10-4V = 0,5mV
Chọn D
Một nguồn sáng điểm được đặt dưới đáy một bể nước sâu 1m. Biết chiết suất của nước là 1,33. Vùng có ánh sáng phát từ điểm sáng ló ra trên mặt nước là
Ta có sinigh = 1/1,33 => igh = 48,750
Tại các điểm có i < igh sẽ có chùm tia sáng ló ra => tani ≤ tan48,750
=> Vùng sáng là hình tròn bán kính R với: R/1 = 1,14m
Chọn C

