Đề thi giữa HK1 môn Vật Lý 12 năm 2020 - Trường THPT Tôn Đức Thắng
Đề thi giữa HK1 môn Vật Lý 12 năm 2020 - Trường THPT Tôn Đức Thắng
-
Hocon247
-
40 câu hỏi
-
60 phút
-
233 lượt thi
-
Trung bình
Tham gia [ Hs Hocon247.com ] - Cộng Đồng Luyện Thi Trực Tuyến để được học tập những kiến thức bổ ích từ HocOn247.com
Trong dao động điều hòa
A đúng
B sai vì vận tốc sớm pha hơn li độ góc π/2
C sai vì gia tốc sớm pha hơn vận tốc góc π/2
D sai vì gia tốc và li độ luôn ngược pha.
Một vật dao động điều hòa theo phương trình: \(x = 3cos\left( {2{\rm{\;}}t + \frac{\pi }{2}} \right){\mkern 1mu} (cm)\)
Tần số của dao động là:
Từ phương trình suy ra tốc độ góc \(\omega = 2{\rm{r}}a{\rm{d}}/s\)
Suy ra tần số của dao động là: \(f = \frac{\omega }{{2\pi }} = \frac{2}{{2\pi }} = \frac{1}{\pi }\left( {Hz} \right)\)
Một vật nhỏ khối lượng m = 0,01kg treo ở đầu một lò xo có độ cứng k = 4 N/m, dao động điều hòa quanh vị trí cân bằng. Chu kì dao động của vật là:
\(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,01}}{4}} = 0,314s\)
Một chất điểm dao động điều hòa trên đoạn thẳng dài 8cm, tần số 5Hz. Lúc t = 0, chất điểm ở vị trí cân bằng và bắt đầu đi theo chiều dương. Phương trình dao động của chất điểm là:
Biên độ dao động của chất điểm là: A= 8/2 =4cm
Tần số góc ω =2πf = 10π rad/s
Khi t = 0, x = 0 và v > 0.
Do đó ta có: cosφ = 0, sinφ < 0
Vậy φ=−π/2
Phương trình dao động của chất điểm là: x = 4cos(10πt−π/2) (cm)
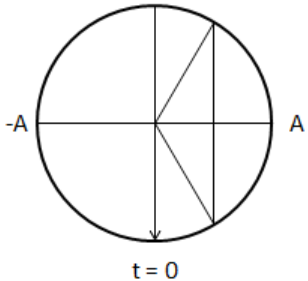
Một con lắc lò xo gồm một quả cầu nhỏ gắn vào đầu một lò xo, dao động điều hòa với biên độ 2,5 cm dọc theo trục Ox, với chu kì 1,2s. Vào thời điểm t = 0, quả cầu đi qua vị trí cân bằng theo chiều dương của trục Ox. Hỏi vào thời điểm nào sau đây quả cầu có li độ x = 1,25 cm?
Ta có: A = 2,5 cm, T = 1,2 s
Thời điểm t = 0 quả cầu đi qua vị trí cân bằng theo chiều dương.
Sử dụng vòng tròn lượng giác:
Suy ra thời điểm quả cầu có li độ x = 1,25 cm = A/2 là:
\(\left[ \begin{array}{l} \varphi = \frac{\pi }{6} \Rightarrow t = \frac{T}{{12}} = \frac{{1,2}}{{12}} = 0,1s\\ \varphi = \frac{{5\pi }}{6} \Rightarrow t = \frac{{5T}}{{12}} = \frac{{5.1,2}}{{12}} = 0,5s \end{array} \right.\)
Một vật dao động điều hòa theo phương trình \(x = 2cos\left( {\pi t - \frac{{3\pi }}{4}} \right)\) trong đó x tính bằng cm, t tính bằng giây (s). Vào thời điểm t =3,5s vật đi qua vị trí có li độ
\(\begin{array}{l} t = 3,5{\rm{s}}\\ \Rightarrow x = 2\cos \left( {\pi .3,5 - \frac{{3\pi }}{4}} \right) = - \sqrt 2 cm \end{array}\)
Một vật nặng treo vào đầu lò xo làm cho lò xo dãn ra 4 cm. Đầu kia treo vào một điểm O cố định. Hệ dao động điều hòa theo phương thẳng đứng.
Cho g = π2 m/s2. Chu kì dao động của hệ là:
\(T = 2\pi \sqrt {\frac{{{\rm{\Delta }}l}}{g}} = 2\pi \sqrt {\frac{{0,04}}{{10}}} = 0,4{\rm{s}}\)
Một con lắc lò xo gồm lò xo có độ cứng k = 100 N/m và vật nặng có khối lượng m, dao động điều hòa theo trục Ox nằm ngang. Thế năng của con lắc đó khi vật đi qua vị trí có li độ x = 3cm theo chiều âm là:
\({{\rm{W}}_t} = \frac{1}{2}k.{x^2} = \frac{1}{2}{.100.0,03^2} = 0,045J\)
Một đầu của lò xo được treo vào điểm cố định O, đầu kia treo một quả nặng m1 thì chu kì T1 = 0,6s. Khi thay đổi quả nặng m2 vào thì chu kì dao động bằng T2 = 0,8s. Chu kì dao động khi treo đồng thời m1 và m2 vào lò xo là:
Chu kì kì dao động của hệ lò xo và vật nặng m1 là:
\({T_1} = 2\pi \sqrt {\frac{{{m_1}}}{k}} \)
Chu kì dao động của hệ lò xo và vật nặng m2 là:
\({T_2} = 2\pi \sqrt {\frac{{{m_2}}}{k}} \)
Chu kì dao động của hệ lò xo và hai vật nặng (m1+m2) là:
\({T_{12}} = 2\pi \sqrt {\frac{{{m_1} + {m_2}}}{k}} \)\( = \sqrt {T_1^2 + T_2^2} = 1s\)
Một con lắc lò xo dao động điều hòa với biên độ A = 10,0cm và cơ năng 0,8J. Độ cứng của lò xo là:
\({\mkern 1mu} k = \frac{{2{\rm{W}}}}{{{A^2}}} = 160N/m\)
Một vật dao động điều hòa, trong thời gian 1 phút vật thực hiện được 30 dao động. Chu kì dao động của vật là:
Ta có:
Số dao động vật thực hiện được trong thời gian t là:
\(t = nT \Leftrightarrow 60 = 30T \Leftrightarrow T = 2s\)
Cho một con lắc lò xo dao động điều hòa với phương trình \(x = 10\cos \left( {20t - \frac{\pi }{3}} \right)\left( {cm} \right)\). Biết vật nặng có khối lượng m = 100g. Động năng của vật tại li độ x = 8cm là:
Ta có:
+ Độ cứng của lò xo:
\(k = m{\omega ^2} = {0,1.20^2} = 40\)
+ Cơ năng:
\({\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}{.40.0,1^2} = 0,2J\)
+ Thế năng tại li độ x = 8cm:
\({{\rm{W}}_t} = \frac{1}{2}k{{\rm{x}}^2} = \frac{1}{2}{.40.0,08^2} = 0,128J\)
+ Động năng của vật tại li độ x = 8cm là:
\({{\rm{W}}_d} = {\rm{W}} - {{\rm{W}}_t} = 0,2 - 0,128 = 0,072J\)
Hiện tượng cộng hưởng cơ học xảy ra khi nào?
Hiện tượng cộng hưởng cơ học xảy ra khi tần số dao động cưỡng bức bằng tần số dao động riêng của hệ.
Một vật treo vào lò xo làm nó dãn ra 4cm. Cho g = π2 ≈ 10 m/s2. Biết lực đàn hồi cực đại, cực tiểu lần lượt là 10N và 6N. Chiều dài tự nhiên của lò xo là 20cm. Chiều dài cực đại và cực tiểu của lò xo trong quá trình dao động là:
Ta có:
\(\begin{array}{l} \left\{ \begin{array}{l} {F_{\max }} = k(\Delta {l_0} + A)\\ {F_{\min }} = k(\Delta {l_0} - A) \end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l} 10 = k(0,04 + A)\,(1)\\ 6 = k(0,04 - A)\,(2) \end{array} \right.\\ \Rightarrow \frac{{10}}{6} = \frac{{0,04 + A}}{{0,04 - A}} \end{array}\)
⇒ A = 0,01m = 1cm
Suy ra:
\(\begin{array}{l} \left\{ \begin{array}{l} {l_{\max }} = {l_0} + \Delta {l_0} + A\\ {l_{\min }} = {l_0} + \Delta {l_0} - A \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} {l_{\max }} = 20 + 4 + 1 = 25cm\\ {l_{\min }} = 20 + 4 - 1 = 23cm \end{array} \right. \end{array}\)
Một vật dao động điều hòa trên quỹ đạo dài 40cm. Khi vật ở vị trí x = 10cm thì vật có vận tốc là v = 20π√3 cm/s. Chu kì dao động của vật là:
Ta có:
- L = 2A =40 ⇒ A = 20cm
- Hệ thức:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \Leftrightarrow {20^2} = {10^2} + \frac{{{{\left( {20\pi \sqrt 3 } \right)}^2}}}{{{\omega ^2}}}\)
\( \Rightarrow \omega = 2\pi \Leftrightarrow T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1s\)
Một vật dao động điều hòa có phương trình dao động là \(x = 5\cos \left( {2\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\) Vận tốc của vật khi có li độ x = 3cm là:
Ta có:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \Leftrightarrow {5^2} = {3^2} + \frac{{{{\left( v \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}\)
\( \Rightarrow v = \pm 8\pi cm/s \approx \pm 25,12cm/s\)
Một vật dao động điều hòa khi đi qua vị trí cân bằng theo chiều dương ở thời điểm ban đầu. Khi vật có li độ 3cm thì vận tốc của vật bằng 8π cm/s và khi vật có li độ bằng 4cm thì vận tốc của vật bằng 6π cm/s. Phương trình dao động của vật có dạng:
Theo bài ra ta có:
Tại thời điểm ban đầu vật đi qua VTCB theo chiều dương
⇒ φ = −π/2 ⇒ φ = −π/2
+ Khi x = 3cm thì v = 8π cm/s, ta có:
\({A^2} = {3^2} + \frac{{{{\left( {8\pi } \right)}^2}}}{{{\omega ^2}}}\) (1)
+ Khi x = 4cm thì v = 6πcm/s, ta có:
\({A^2} = {4^2} + \frac{{{{\left( {6\pi } \right)}^2}}}{{{\omega ^2}}}\) (2)
Giải hệ phương trình (1) và (2) ta được:
\(\left\{ \begin{array}{l} \omega = 2\pi \\ A = 5cm \end{array} \right.\)
Vậy phương trình dao động của vật có dạng:
\(x = 5\cos \left( {2\pi t - \frac{\pi }{2}} \right)\left( {cm} \right)\)
Một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số có phương trình: \({x_1} = 3\cos \left( {10\pi t + \frac{\pi }{6}} \right)\left( {cm} \right)\) và \({x_2} = 7\cos \left( {10\pi t + \frac{{13\pi }}{6}} \right)\left( {cm} \right)\). Dao động tổng hợp có phương trình là:
Dao động tổng hợp có dạng:
\(\begin{array}{*{20}{l}} {x = {x_1} + {x_2} = 3\cos \left( {10\pi t + \frac{\pi }{6}} \right) + 7\cos \left( {10\pi t + \frac{{13\pi }}{6}} \right)}\\ { = 10\cos \left( {10\pi t + \frac{\pi }{6}} \right)\left( {cm} \right)} \end{array}\)
Một con lắc lò xo dao động điều hòa với phương trình \(x = 10\cos \omega t\left( {cm} \right)\). Tại vị trí có li độ x = 5cm, tỉ số giữa động năng và thế năng của con lắc là:
Ta có:
Tại vị trí x = 5cm =A/2
+ Thế năng:
\({{\rm{W}}_t} = \frac{1}{2}k{{\rm{x}}^2} = \frac{1}{2}k{.0,05^2} = {1,25.10^{ - 3}}k\left( J \right)\)
+ Cơ năng:
\({\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}k{.0,1^2} = {5.10^{ - 3}}k\left( J \right)\)
+ Động năng:
\({{\rm{W}}_d} = {\rm{W}} - {{\rm{W}}_t} = \left( {5 - 1,25} \right){.10^{ - 3}}k = {3,75.10^{ - 3}}k\left( J \right)\)
Suy ra tỉ số:
\(\frac{{{{\rm{W}}_d}}}{{{{\rm{W}}_t}}} = \frac{{{{3,75.10}^{ - 3}}k}}{{{{1,25.10}^{ - 3}}k}} = 3\)
Cho một con lắc lò xo dao động với phương trình \(x = 10\cos \left( {20t - \frac{\pi }{3}} \right)\left( {cm} \right)\). Biết vật nặng có khối lượng m = 100g. Thế năng của con lắc tại thời điểm t = π(s) bằng:
Tại thời điểm t =π vật có li độ là:
\(x = 10\cos \left( {20\pi - \frac{\pi }{3}} \right) = 5cm\)
Độ cứng của lò xo là:
\(k = m{\omega ^2} = {0,1.20^2} = 40\)
Thế năng của lò xo tại thời điểm t=π là:
\({{\rm{W}}_t} = \frac{1}{2}k{{\rm{x}}^2} = \frac{1}{2}{.40.0,05^2} = 0,05J\)
Khi quả nặng của một con lắc đơn đi từ vị trí cân bằng đến vị trí biên thì nhận định nào dưới đây là sai?
Khi quả nặng của một con lắc đơn đi từ vị trí cân bằng đến vị trí biên thì lực căng của sợi dây giảm.
Trong dao động cưỡng bức hiện tượng cộng hưởng xảy ra khi
Trong dao động cưỡng bức, hiện tợng cộng hưởng xảy ra khi tần số của lực cưỡng bức bằng tần số riêng của hệ dao động.
Trong một dao động điều hòa, khi biết tần số góc ω,ω, biên độ A. Công thức liên hệ giữa vận tốc v của vật với li độ của vật ở cùng thời điểm có dạng
Công thức liên hệ:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} \Rightarrow \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} - {x^2}\)
Một con lắc lò xo có độ cứng k treo thẳng đứng, đầu trên gắn cố định còn đầu dưới treo quả cầu nhỏ ở nơi có gia tốc trọng trường g. Khi vật ở vị trí cân bằng lò xo có độ dãn Δl. Cho con lắc dao động điều hòa theo phương thẳng đứng với biên độ A (A>Δl). Lực đàn hồi (F) của lò xo có độ lớn nhỏ nhất trong quá trình dao động là
Ta có: Δl< A
=> trong quá trình dao động lò xo dãn khi x<−Δl, lò xo nén khi x<Δl
⇒ Fdhmin=0 tại vị trí x =−Δl
Một con lắc đơn dao động với biên độ góc nhỏ \(\\sin {\alpha _0} \approx {\alpha _0}(rad).\)Tần số dao động của nó được tính bằng công thức
Tần số dao động của con lắc đơn:
\(f = \frac{\omega }{{2\pi }} = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \)
Tại một vị trí dao động, nếu tăng chiều dài của con lắc đơn lên 2 lần thì tần số dao động của con lắc sẽ
\(\left\{ \begin{array}{l} f = \frac{1}{{2\pi }}\sqrt {\frac{g}{l}} \\ f' = \frac{1}{{2\pi }}\sqrt {\frac{g}{{2l}}} \end{array} \right. \Rightarrow \frac{f}{{f'}} = \sqrt 2 \Leftrightarrow f' = \frac{1}{{\sqrt 2 }}f\)
Một con lắc đơn với dây treo có độ dài l được thả không vận tốc ban đầu từ vị trí có biên độ góc α0. Tốc độ của con lắc khi nó đi qua vị trí có li độ góc α được tính bằng công thức:
Tốc độ của con lắc đơn khi nó đi qua vị trí có li độ αđược tính bằng công thức:
\(v = \sqrt {2gl\left( {\cos \alpha - \cos {\alpha _0}} \right)} \)
Một vật dao động điều hòa theo phương trình \(x = 20cos(2\pi t + \pi ){\mkern 1mu} (cm).\)Thời điểm để vật đi qua vị trí có li độ x = 10√2cm theo chiều âm quy ước là:
Chu kì T = 2π/ω = 1s
Ta có: x=10√2=A√2/2
Tại thời điểm t = 0 vật ở vị trí biên âm
=> thời điểm vật qua vị ví có li độ x = 10√2 theo chiều âm vật quay được góc φ =5π/4
=> t = 5T/8 = 5/8 s
Một con lắc lò xo có khối lượng m = 20g, được kích thích cho dao động với phương trinh \(x = 10cos(10t){\mkern 1mu} (cm).\). Năng lượng đã truyền cho vật là:
\({\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}{.0,2.10^2}{.0,1^2} = 0,1J\)
Hai lò xo k1, k2 có cùng độ dài. Một vật nặng khi treo vào lò xo k1 thì dao động với chu kì T1 = 0,3s, khi treo vào lò xo k2 thì dao động với chu kì T2 = 0,4s. Ghép song song hai lò xo đó với nhau rồi treo vật nặng đó vào thì chu kì dao động của vật là:
Chu kì dao động của hệ lò xo khi treo vật nặng vào lò xo k1 là:
\({T_1} = 2\pi \sqrt {\frac{m}{{{k_1}}}} \)
Chu kì dao động của hệ lò xo khi treo vật nặng vào lò xo k2 là:
\({T_2} = 2\pi \sqrt {\frac{m}{{{k_2}}}} \)
Chu kì dao động của hệ lò xo khi treo vật nặng vào lò xo k1, k2 ghép song song là:
\({T_{12}} = 2\pi \sqrt {\frac{m}{k}} ,\)
\(k = {k_1} + {k_2} \Rightarrow \frac{1}{{T_1^2}} + \frac{1}{{T_2^2}}\)
\( \Rightarrow {T_{12}} = \frac{{{T_1}.{T_2}}}{{\sqrt {T_1^2 + T_2^2} }} = 0,24s\)
Một vật treo vào một lò xo làm lò xo dãn 5cm. Biết lực đàn hồi tác dụng lên vật là 1N, độ cứng của lò xo là:
\(F = k{\rm{\Delta }}l \Leftrightarrow k = \frac{F}{{{\rm{\Delta }}l}} = \frac{1}{{{{5.10}^{ - 2}}}} = 20N/m\)
Một con lắc lò xo gồm vật nặng có khối lượng m = 100g và lò xo có độ cứng k = 60 N/m. Vật nặng của con lắc được kích thích cho dao động điều hòa với biên độ 4cm. Nếu bỏ qua mọi lực cản thì gia tốc cực đại của vật khi dao động bằng
\({a_{max}} = {\omega ^2}A = \frac{k}{m}.A = \frac{{60}}{{0,1}}.0,04 = 24{\mkern 1mu} m/{s^2}\)
Một vật tham gia đồng thời hai dao động điều hòa, cùng phương, cùng tần số, cùng biên độ là A và lệch pha nhau π/2. Biên độ dao động tổng hợp của hai dao động trên bằng
Hai dao động vuông pha, biên độ dao động tổng hợp là:
\(A = \sqrt {A_1^2 + A_2^2} = \sqrt {{A^2} + {A^2}} = A\sqrt 2 \)
Một vật dao động điều hòa có chu kì là T. Nếu chọn gốc thời gian t = 0 là lúc vật đạt li độ cực đại, thì trong nửa chu kì đầu tiên, vận tốc của vật đạt giá trị cực đại ở thời điểm
Tại thời điểm t = 0 vật ở vị trí biên, vật đạt vận tốc cực đại tại VTCB.
Từ vị trí biên đến VTCB vật quay góc π/2 ⇒ t = T/4
Một con lắc lò xo đang dao động tắt dần. Người ta đo được độ giảm tương đối của biên độ trong hai chu kì đầu tiên là 7,5%. Độ giảm thế năng tương ứng là:
Theo đề bài ta có:
\(\frac{{{\rm{\Delta }}A}}{{{A_0}}} = 7,5{\rm{\% }} \Rightarrow {\rm{\Delta }}A = 0,075{{\rm{A}}_0}\)
\({\rm{\Delta }}A = {A_0} - {A_1} \Leftrightarrow {A_1} = {A_0} - {\rm{\Delta }}A = 0,925{{\rm{A}}_0}\)
Độ giảm tương đối của thế năng được xác định bằng:
\(\begin{array}{l} \frac{{{\rm{\Delta W}}}}{{\rm{W}}} = \frac{{\frac{1}{2}kA_0^2 - \frac{1}{2}kA_1^2}}{{\frac{1}{2}{\rm{kA}}_0^2}} = \frac{{A_0^2 - A_1^2}}{{A_0^2}}\\ = \frac{{A_0^2 - {{\left( {0,925{{\rm{A}}_0}} \right)}^2}}}{{A_0^2}} = 0,14 = 14{\rm{\% }} \end{array}\)
Một con lắc lò xo gồm lò xo có độ cứng 30 N/m và vật nặng có khối lượng 0,3kg dao động điều hòa. Tại thời điểm t, vận tốc và gia tốc của vật là 40 cm/s và 3 m/s2. Biên độ dao động của vật là:
\(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{30}}{{0,3}}} = 10\sqrt 3 rad/s\)
Áp dụng công thức:
\(\frac{{{a^2}}}{{{\omega ^4}{A^2}}} + \frac{{{v^2}}}{{{\omega ^2}{A^2}}} = 1,\)
ta tìm được: A = 5cm.
Một vật dao động điều hòa, biết rằng cứ sau những khoảng thời gian 0,05s thì động năng của vật lại bằng thế năng. Chu kì dao động của vật là:
Sau T/4 thì động năng của vật lại bằng thế năng
⇒ T = 4.0,05 = 0,20s
Một vật tham gia đồng thời hai dao động điều hòa, cùng phương, cùng tần số, với các phương trình: \({x_1} = 3cos(\omega t);{\mkern 1mu} {x_2} = 3\sin (\omega t + \pi ){\mkern 1mu} (cm).\).
Phương trình dao động tổng hợp của vật là:
Phương trình dao động tổng hợp:
\(x = {x_1} + {x_2} = 3\sqrt 2 \cos \left( {\omega t + \frac{\pi }{4}} \right)\left( {cm} \right)\)
Tần số của năng lượng trong dao động tuần hoàn theo thời gian
Tần số của năng lượng trong dao động tuần hoàn theo thời gian bằng 2 lần tần số li độ
Chu kỳ của con lắc lò xo dao động điều hòa
Chu kỳ của con lắc lò xo không phụ thuộc vào biên độ dao động.